
- •Силлабус
- •1. Сведения о преподавателе:
- •4. Пререквизиты и постреквизиты учебной дисциплины
- •5. Характеристика учебной дисциплины
- •6. Список литературы Основная литература:
- •Дополнительная литература:
- •7. Контроль и оценка результатов обучения
- •8. Политика учебной дисциплины
- •Частные производные и дифференцируемость функций нескольких переменных.
- •Двойные и тройные интегралы.
- •Криволинейные интегралы
- •Векторные и скалярные поля
- •Числовые ряды.
- •Признаки сходимости рядов
- •Степенные ряды. Интервал сходимости степенного ряда. Разложение функций в степенные ряды.
- •Свойства степенных рядов.
- •Лекции 13-21. Дифференциальные уравнения
- •§ 2. Простейшее дифференциальное уравнение
- •§ 3. Уравнение с разделяющимися переменными
- •§ 4. Однородные уравнения
- •§ 5. Обобщенное однородное уравнение
- •§ 6. Линейное уравнение первого порядка
- •§ 7. Уравнение в полных дифференциалах
- •§ 8. Уравнение Бернулли
- •§ 9. Линейные дифференциальные уравнения с постоянными коэффициентами
- •Уравнение Эйлера
- •Уравнения первого порядка, не разрешенные относительно производной
- •1°. Уравнение, содержащее только :
- •2°. Уравнение, не содержащее искомой функции:
- •3°. Уравнение, не содержащее независимой переменной:
- •3°. Уравнение Лагранжа:
- •4°. Уравнение Клеро:
- •§12. Системы обыкновенных дифференциальных уравнений
- •План решения системы (12.1) методом Эйлера :
- •Теория вероятностей Введение
- •Вероятность и риск, пространство элементарных событий
- •Элементы комбинаторики
- •Вероятность события. Классическое определение
- •Статистическое (частотное) определение вероятности. Теорема сложения вероятностей
- •Формула полной вероятности
- •Среднее арифметическое, мода и медиана. Среднее квадратическое отклонение
- •Значения t-критерия Стьюдента для вероятности 0,95 и 0,99
- •Лекции 27-30. Задачи математической статистики. Выборочный метод. Эмпирическая функция распределения. Полигон и гистограмма.
- •Список рекомендуемой литературы Основная литература:
- •Дополнительная литература:
- •Планы проведения семинарских занятий.
- •Материалы для самостоятельной работы студента (срс)
- •Тестовые задания для самоконтроля
- •Тема: «Функции многих переменных».
- •Тестовые задания для самоконтроля
3°. Уравнение, не содержащее независимой переменной:
![]() (11.2)
(11.2)
Рассмотрим два случая.
1. Уравнение (11.2)
разрешимо относительно
![]()
![]()
Тогда
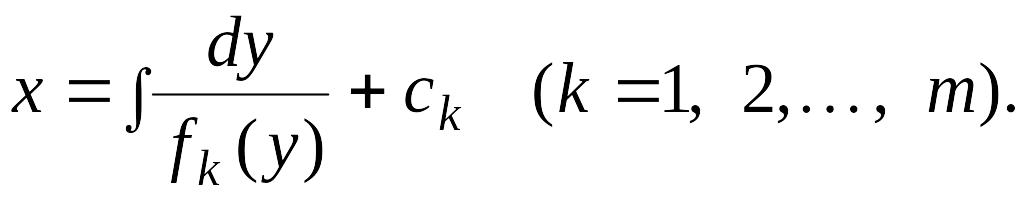
П. 11.6
![]()
Разрешаем уравнение
относительно
![]()
![]()
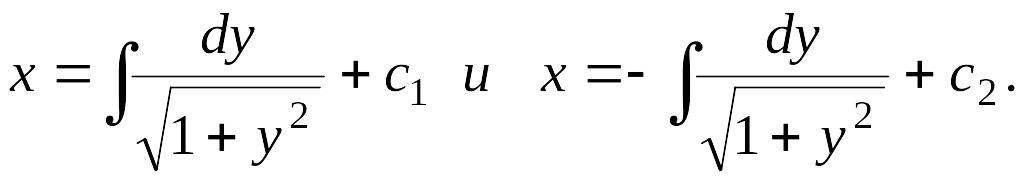 Интегрируя, находим
общее решение
Интегрируя, находим
общее решение
![]() и
и
![]()
2. Уравнение (11.2) не разрешимо (в элементарных функциях) относительно но допускает параметрическое представление:
![]()
Тогда
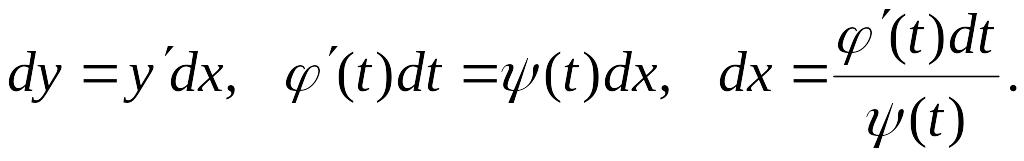
Общее решение в параметрической форме:
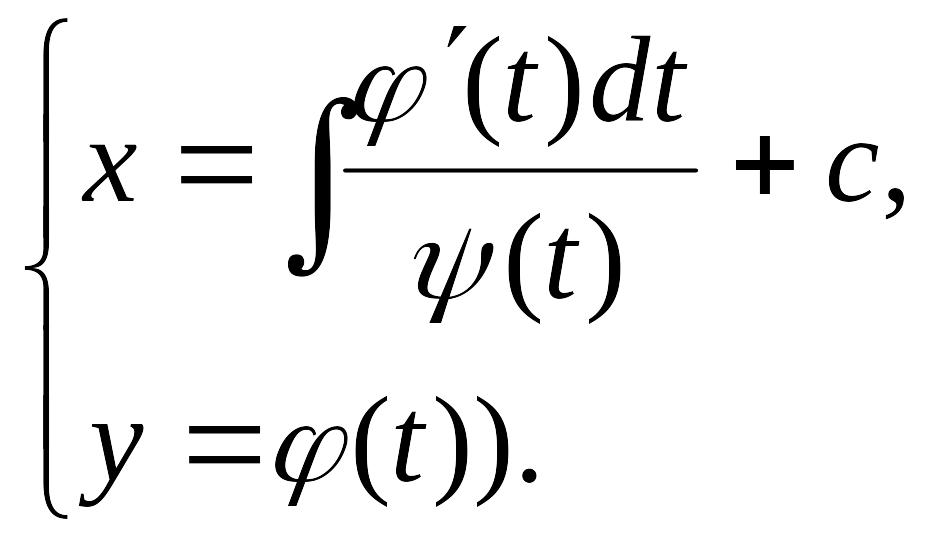
П. 11.7
![]()
Полагаем
![]() Тогда
Тогда
![]()
![]()
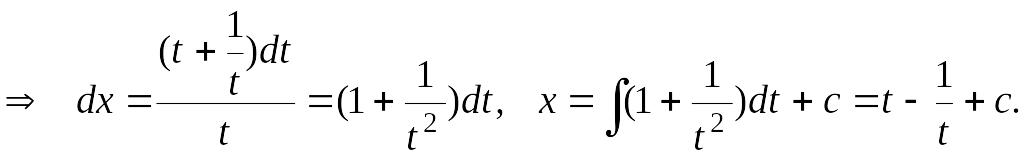 Общее решение в
параметрической форме:
Общее решение в
параметрической форме:
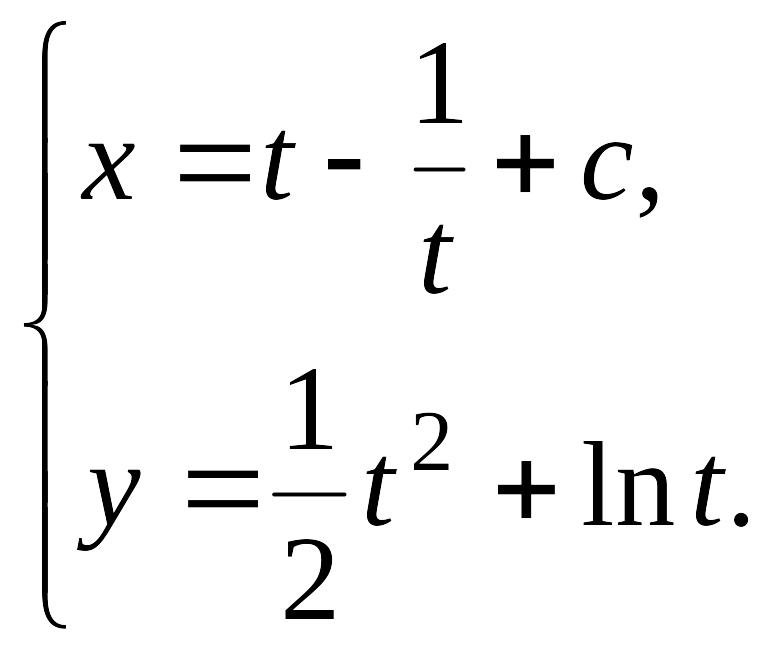
3°. Уравнение Лагранжа:
![]()
Положим
![]() тогда
тогда
![]() Считаем, что
Считаем, что
![]()
Поэтому
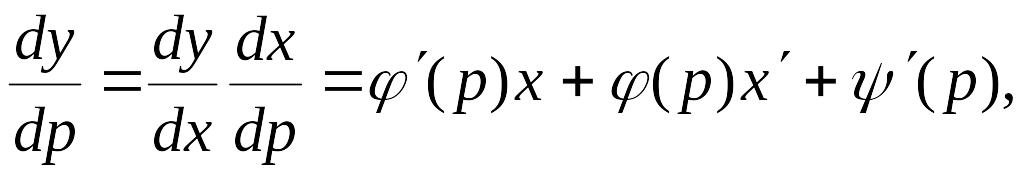 или
или
![]()
1).
![]() тогда
тогда
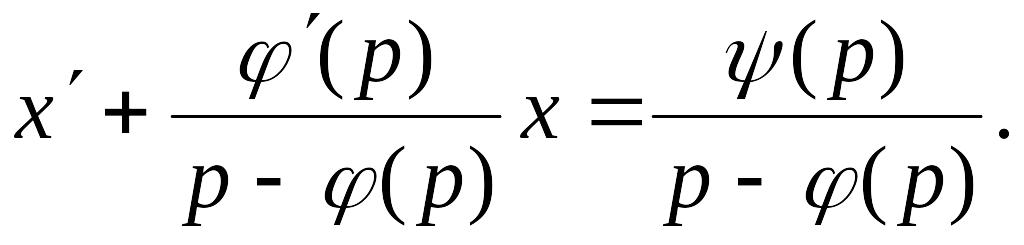 Получили линейное уравнение. Пусть его
решение
Получили линейное уравнение. Пусть его
решение
![]() Тогда общее решение можно записать в
пара-метрической форме:
Тогда общее решение можно записать в
пара-метрической форме:
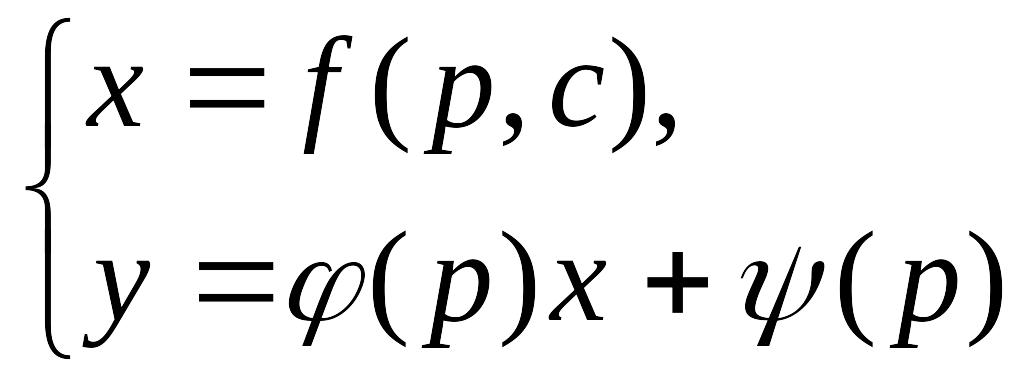
2).
![]() пусть
пусть
![]() корни этого уравнения, тогда получаем:
корни этого уравнения, тогда получаем:
![]() .
Эти прямые линии могут оказаться
осо-быми решениями уравнения Лагранжа.
.
Эти прямые линии могут оказаться
осо-быми решениями уравнения Лагранжа.
П. 11.8
![]()
Делаем замену
тогда
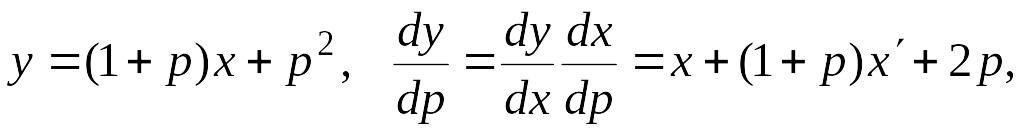
![]() Делаем замену
Делаем замену
![]()
![]()
![]() Таким образом,
общее решение в пара-метрической форме:
Таким образом,
общее решение в пара-метрической форме:
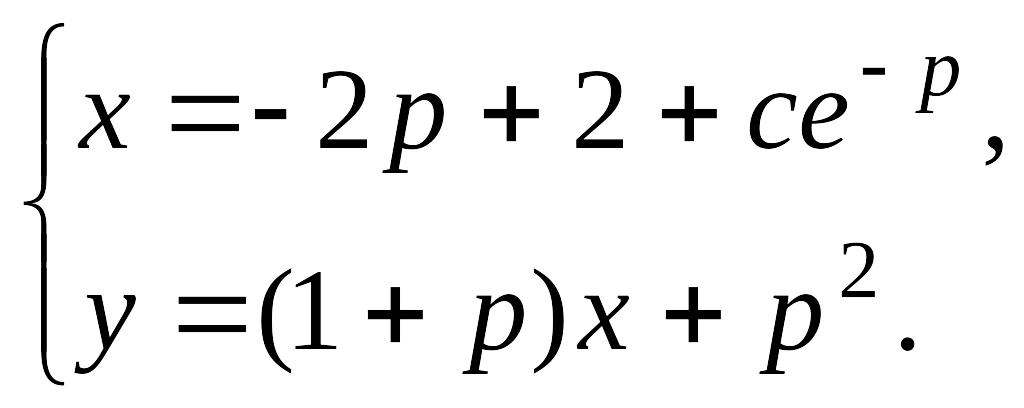
4°. Уравнение Клеро:
![]()
Делаем замену
тогда
![]()
Далее
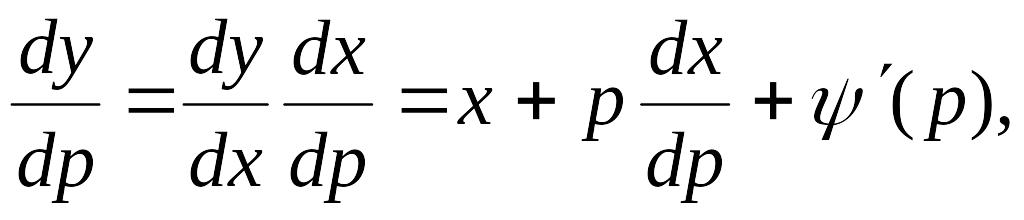
![]()
Уравнение
распадается на два:
![]()
Из первого
уравнения следует, что p=c и, значит,
![]() Это семейство прямых линий является
общим решением.
Это семейство прямых линий является
общим решением.
Уравнение
![]() вместе с уравнением
вместе с уравнением
![]() доставляют ре-шение уравнения Клеро в
параметрической форме:
доставляют ре-шение уравнения Клеро в
параметрической форме:
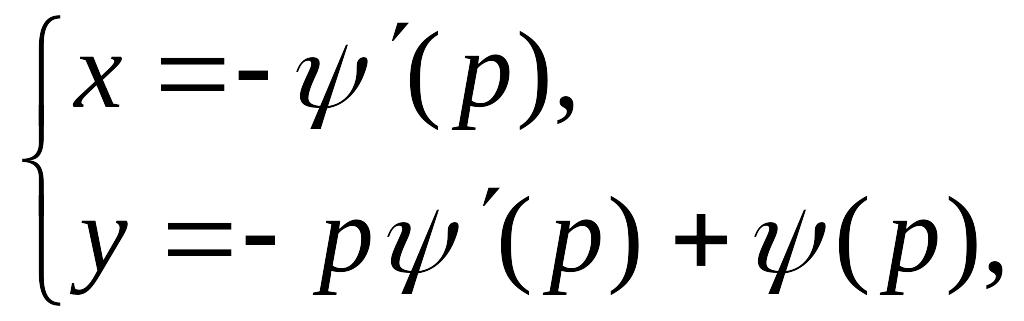
которое обычно
является особым решением, причем оно
заведомо будет особым, если
![]() сохраняет знак.
сохраняет знак.
П. 11.9
![]()
Делаем замену
тогда
![]()
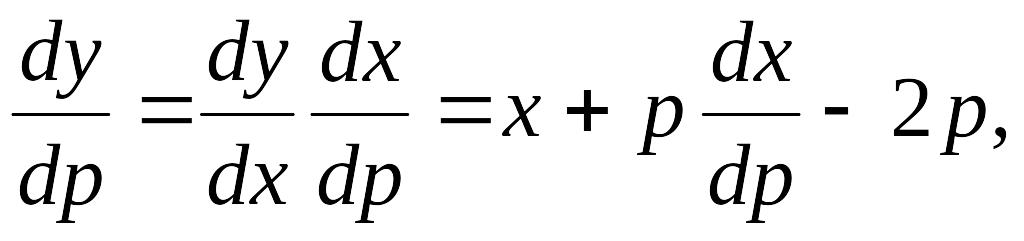
![]() Уравнение распадается на два:
Уравнение распадается на два:
![]() Общее решение:
Общее решение:
![]() Из второго уравнения находим:
Из второго уравнения находим:
![]()
![]()
Исключая параметр
p, получаем особое решение в явном
виде:
![]()
П. 11.10
![]()
Делаем замену
тогда
![]()
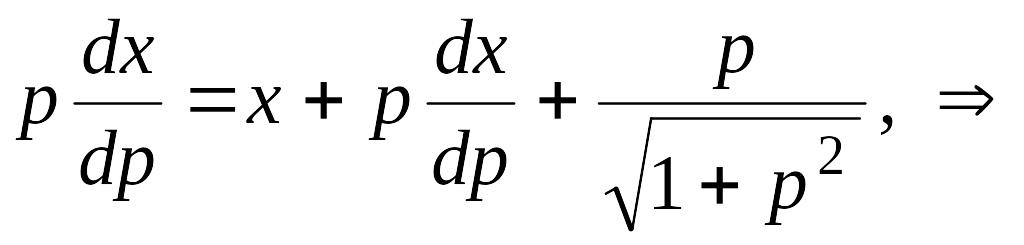
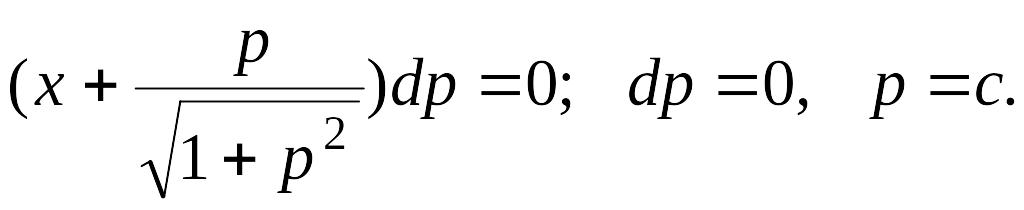 Общее решение:
Общее решение:
![]() Далее,
Далее,
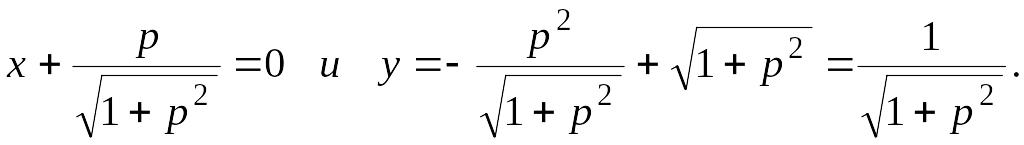 Исключая из этих
урав-нений параметр p, находим
особое решение в виде
Исключая из этих
урав-нений параметр p, находим
особое решение в виде
![]()
§12. Системы обыкновенных дифференциальных уравнений
1°. Система дифференциальных уравнений
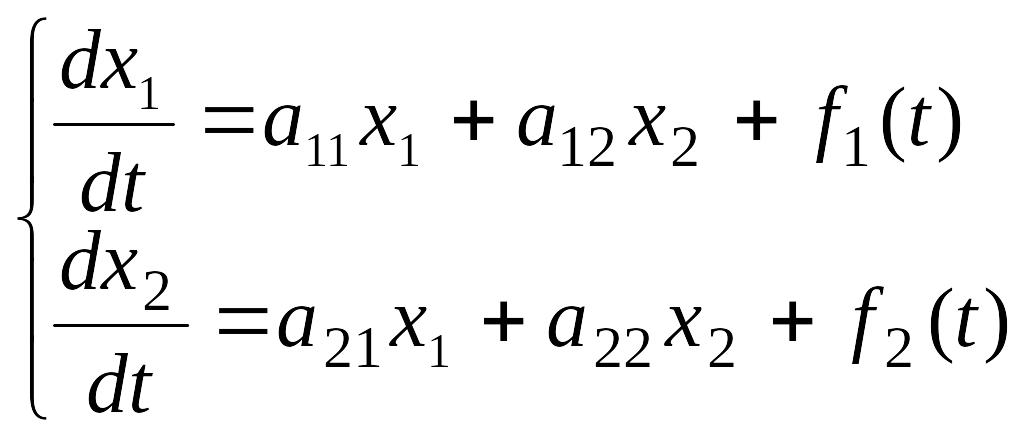 ,
,
где
![]() - искомые функции от t;
- искомые функции от t;
![]() - постоянные числа;
- постоянные числа;
![]() - заданные
- заданные
функции, называется системой линейных дифференциальных уравнений с постоянными коэффициентами второго порядка.
Такую систему методом исключения можно привести к одному линейному урав-нению не выше второго порядка. Решение этой задачи рассмотрим на примерах.
П. 12.1
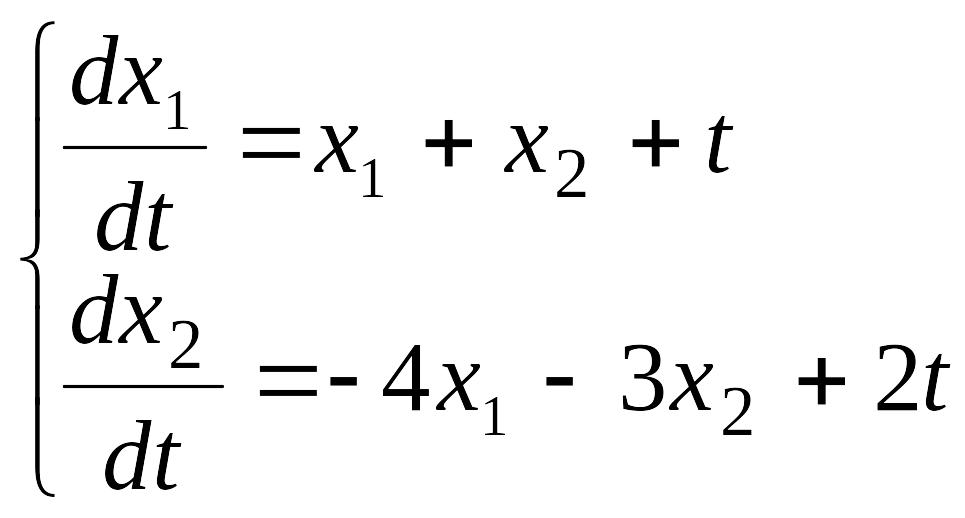
Дифференцируем
первое уравнение по t
:
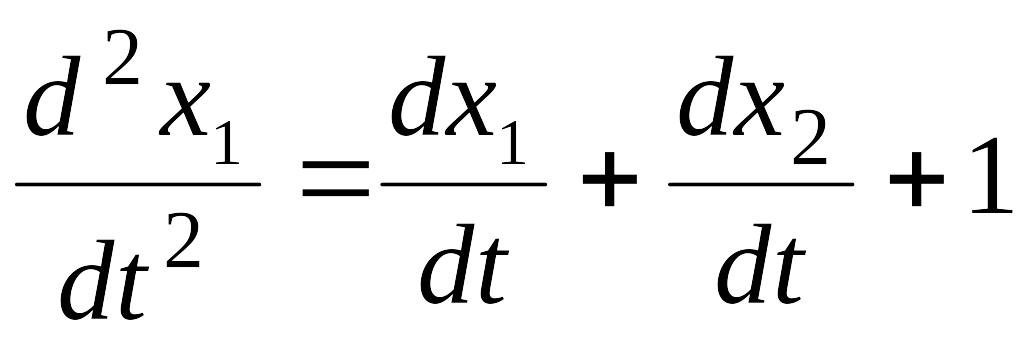 .
Подставляем сюда из
.
Подставляем сюда из
системы уравнений
производные
![]() :
:
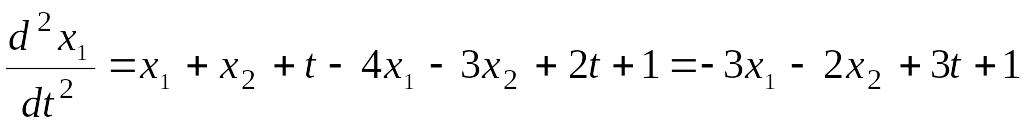 .
Из первого уравнения системы
.
Из первого уравнения системы
![]() ,
тогда
,
тогда
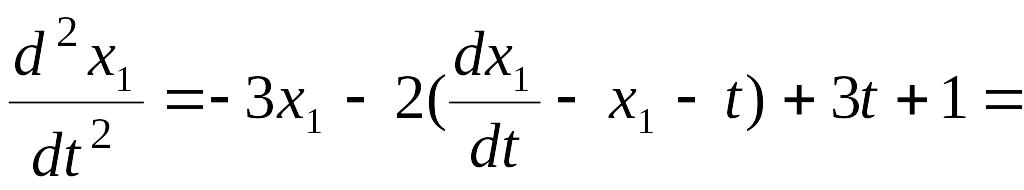
![]() .
Т .о.,
.
Т .о.,
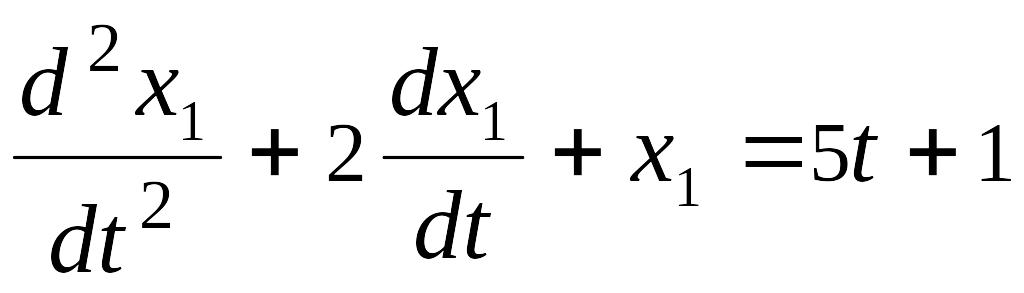 - линейное уравнение; решая его известным
способом, найдем
- линейное уравнение; решая его известным
способом, найдем
![]() ;
далее,
;
далее,
![]() находим из соотношения
находим из соотношения
![]()
![]() .
Общее решение системы :
.
Общее решение системы :
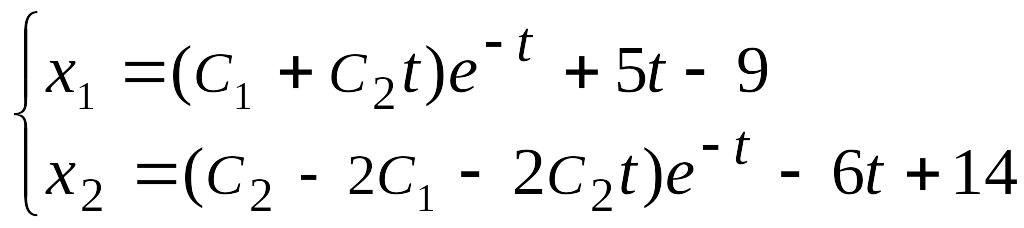 .
.
Решим задачу Коши
с начальными данными :
![]() .
.
![]()
![]() .
.
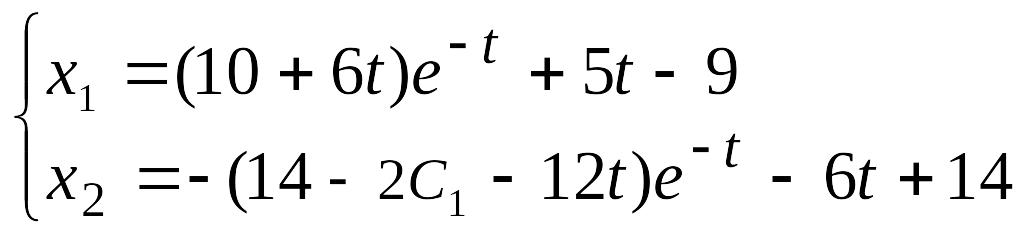 .
.
2°. Система дифференциальных уравнений
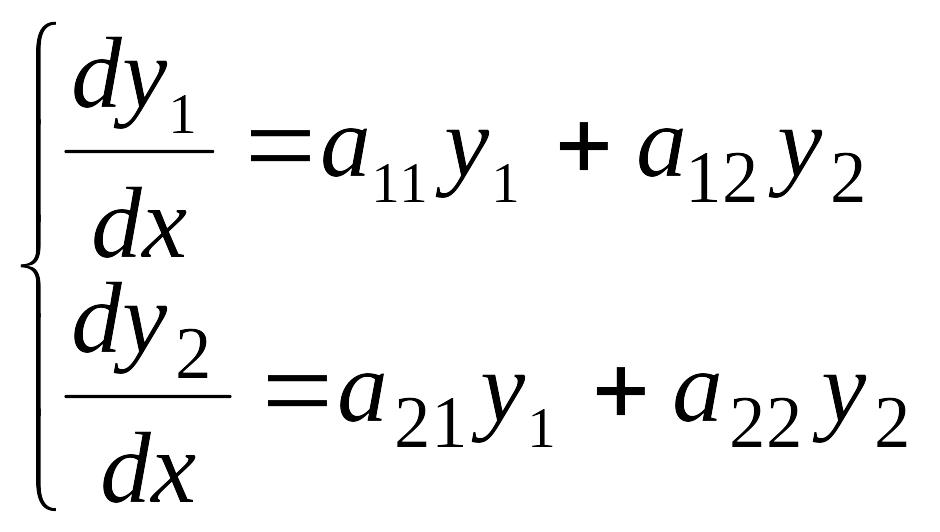 ,
(12.1)
,
(12.1)
где
![]() - искомые функции от x
;
- постоянные числа; называется системой
линейных однородных дифференциальных
уравнений с постоянными коэффициентами
второго порядка.
- искомые функции от x
;
- постоянные числа; называется системой
линейных однородных дифференциальных
уравнений с постоянными коэффициентами
второго порядка.
Систему можно, конечно, решить методом исключения, но можно решить более универсальным методом (методом Эйлера).
Если для системы (12.1) известна система линейно независимых частных решений (фундаментальная система решений):
![]()
![]()
тогда общее решение
имеет вид
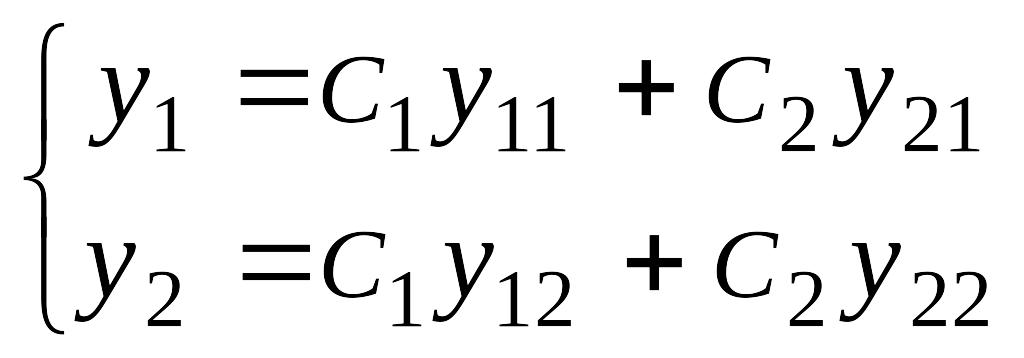 .
(12.2)
.
(12.2)
Частные решения
ищем в виде :
![]() .
После подстановки
.
После подстановки
![]() в систему и сокращении на
в систему и сокращении на
![]() получаем систему уравнений для определения
неизвестных
получаем систему уравнений для определения
неизвестных
![]() :
:
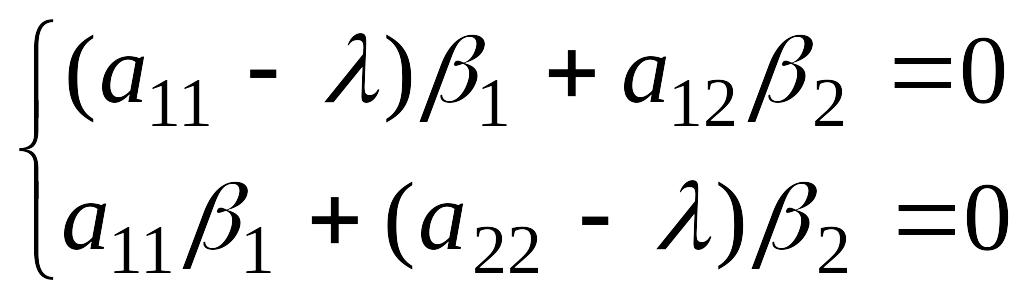 (12.3)
(12.3)
Чтобы эта однородная линейная система алгебраических уравнений имела ненулевое решение должно выполняться условие :
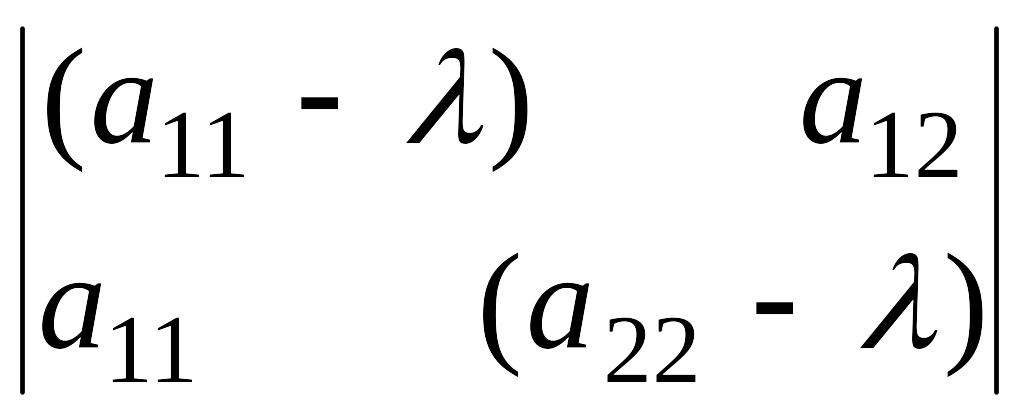 =0
(12.4)
=0
(12.4)
Уравнение (12.4) называется характеристическим уравнением, а его корни -
характеристическими числами.
