§ 8. Уравнение Бернулли

Дифференциальное уравнение

,

где - функции от определенные и непрерывные в некотором интервале , , называется уравнением Бернулли.

Уравнение Бернулли приводится к линейному путем деления обеих частей уравнения на с последующей заменой .

П. 8.1

Делим обе части уравнения на : . Делаем замену ,

, - линейное уравнение. Делаем замену . Выбираем так, чтобы , . Т. о. , . Пусть , тогда,

.

Т.о. , - общее решение.

П. 8.2

Делим обе части уравнения на : . Делаем замену ,

, , - линейное уравнение. Делаем замену

, Выбираем так, чтобы Т. о. , при выбранном , - общее решение.

.

П. 8.3 . Начальные данные

Делим обе части уравнения на : . Делаем замену ,

, . Деля обе части последнего уравнения на - , получаем линейное уравнение . Делаем замену . Выбираем так, чтобы =0, . Т. о. , при выбранном . Беря по частям интеграл, находим .

Значит, . Находим , 1=1-0+c, c=0.

Итак, - решение, отвечающее начальным данным.

§ 9. Линейные дифференциальные уравнения с постоянными коэффициентами

Уравнение

(9.1) называется линейным дифференциальным уравнением n-го порядка с постоянными ко-эффициентами; - постоянные вещественные числа. Если функция ) не равна тождественно нулю, то иногда говорят, что уравнение с правой частью.

Уравнение

(9.2) называется линейным однородным дифференциальным уравнением n-го порядка с постоянными коэффициентами; - постоянные вещественные числа. Т. к. функция ) равна тождественно нулю, то иногда говорят, что уравнение без правой части.

Уравнение (9.3)

называется характеристическим уравнением, а его корни – характеристическими числами уравнения (9.2).

Система функций называется линейно независимой в интервале , если тождество ( - постоянные числа)

может выполняться только когда все . Если к тому же каждая из функций является частным решением однородного уравнения (9.2), то система решений однородного уравнения называется фундаментальной системой решений.

Если фундаментальная система решений найдена, то функция

дает общее решение однородного уравнения (9.2), ( все - константы ).

1°. Однородное уравнение. Рассмотрим три случая.

(♠) Все корни характеристического уравнения различны и вещественны.

Фундаментальная система решений имеет вид :

.

Функция дает общее решение одно-родного уравнения (9.2) ( все - константы ).

П. 9.1 .

Записываем характеристическое уравнение . Его корни ,

; фундаментальная система решений ;

- общее решение.

П. 9.2 . Начальные данные: при .

Корни характеристического уравнения . Общее ре-шение . Т. к. , то для определения костант

имеем два уравнения: . Значит, - частное решение, удовлетворяющее заданным начальным данным.

(♠♠) Все корни характеристического уравнения различны, но среди них есть

комплексные.

Каждому вещественному корню по-прежнему соответствует частное решения , а каждой паре комплексных сопряженных корней соответствуют два линейно-независимых частных решения :

.

Т.о., фундаментальную систему решений в данном случае образуют линейно-независимые частные решения, которые соответствуют вещественным корням, и линейно-независимые частные решения, которые соответствуют каждой паре комплексно-сопряженных корней.

Общее решение дает линейная комбинация фундаментальной системы решений с произвольными постоянными коэффициентами .

П. 9.3

Находим корни характеристического уравнения или

. Один корень вещественный и пара комплексно-сопряженных корней (a=0, b=3, т. е. корни чисто мнимые ). Фундаментальная система решений : . Записываем общее решение

.

П. 9.4

Характеристическое уравнение: ,

, ( a=3, b=2 ). Фундаментальная система решений :

.

Общее решение .

П. 9.5 . Начальные данные: при .

Корни характеристического уравнения .

Фундаментальная система решений : .

Общее решение . Для определения констант находим .

.

При . Т.о. , частное решение, удов-летворяющее заданным начальным условиям, имеет следующий вид:

.

(♠♠♠) Среди корней характеристического уравнения имеются кратные корни.

В этом случае каждому вещественному корню кратности k соответствует k линейно-независимых частных решений вида

,

причем в формулу общего решения будет привнесен вклад в виде линейной комбинации

,

а каждой паре комплексных сопряженных корней кратности k соответствуют 2k линейно-независимых частных решения вида

В формулу общего решения будет привнесен вклад в виде линейной комбинации

.

Т.о., фундаментальную систему решений в данном случае образуют линейно-независимые частные решения, которые соответствуют вещественным простым и кратным корням, и линейно-независимые частные решения, которые соответствуют каждой паре простых и кратных комплексно-сопряженных корней.

Общее решение дает линейная комбинация фундаментальной системы решений с произвольными постоянными коэффициентами .

П. 9.6

Корни характеристического уравнения кратны, . Кратность вещественного корня . Фундаментальная система

решений : . Общее решение .

П. 9.7

Корни характеристического уравнения комплексны и кратны, . Кратность пары комплексно-сопря-женных корней , (a=0, b=2, т. е. корни чисто мнимые ). Фундаментальная система решений : .

Общее решение .

П. 9.8

Характеристическое уравнение имеет двукратный вещественный корень и пару комплексно-сопряженных корней , . Фундаментальная система решений : .

Общее решение .

П. 9.9

Характеристическое уравнение имеет простой вещественный корень и двукратную пару комплексно-сопряженных корней , корни чисто мнимые).

Фундаментальная система решений : .

Общее решение .

2°. Неоднородное уравнение. Общее решение неоднородного дифференциального уравнения с постоянными коэффициентами

можно найти по формуле (формула верна и в том случае, когда коэффициенты не являются константами) , где - частное решение неоднородного уравнения, а

- общее решение однородного уравнения .

Т.о., чтобы найти общее решение неоднородного уравнения , надо

найти общее решение однородного уравнения и частное решение

неоднородного .

Стало быть, возникает задача нахождения частного решения неоднородного уравнения. Рассмотрим четыре случая решения задачи методом неопределенных коэффициентов, когда правая часть имеет специальный (стандартный ) вид.

Суть метода заключается в том, что частное решение ищут в заранее известном виде с неопределенными коэффициентами, конкретные значения которых находят подстановкой в исходное уравнение и приравниванием коэффициентов при одинаковых функциях в левой и правой частях.

(♠) , где - полином от степени (который, в частности, может быть константой, не равной нулю).

Если число 0 не является корнем характеристического уравнения, то следует искать в виде

,

где - полином той же степени с неопределенными коэффициентами.

Если же число 0 является корнем характеристического уравнения кратности , то следует искать в виде

.

П. 9.10

Корни характеристического уравнения . Общее решение однородного уравнения . Число 0 не является корнем характеристи-ческого уравнения частное решение ищем в виде . Теперь сог-ласно рецепту следует подставить в исходное уравнение, однако обычно придерживаются нижеследующей схеме.

-1
0
1

Во втором столбце стоят и производные, в первом - коэффициенты, с которыми входят в уравнение; в третьем столбце приравнены коэффициенты при одинаковых функциях в левой и правой частях уравнения; в четвертом столбце приведены значения найденных неопределенных коэффициентов. Т.о., частное решение

.

Общее решение .

П. 9.11

Корни характеристического уравнения . Общее решение однородного уравнения . Число 0 является корнем характеристического уравнения кратности частное решение ищем в виде . Далее, согласно схеме.

0
-4
1

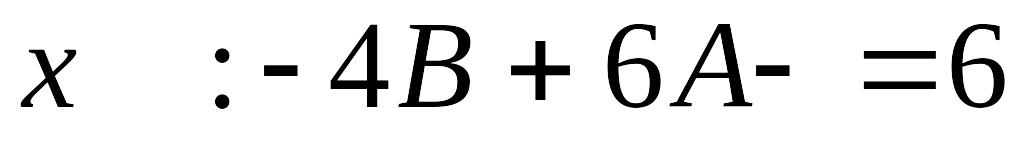
Т.о., . Общее решение .

П. 9.12

Корни характеристического уравнения . Число 0 является корнем характеристического уравнения кратности . Общее решение одно-родного уравнения . Частное решение ищем в виде . Далее, согласно схеме.

0
-1
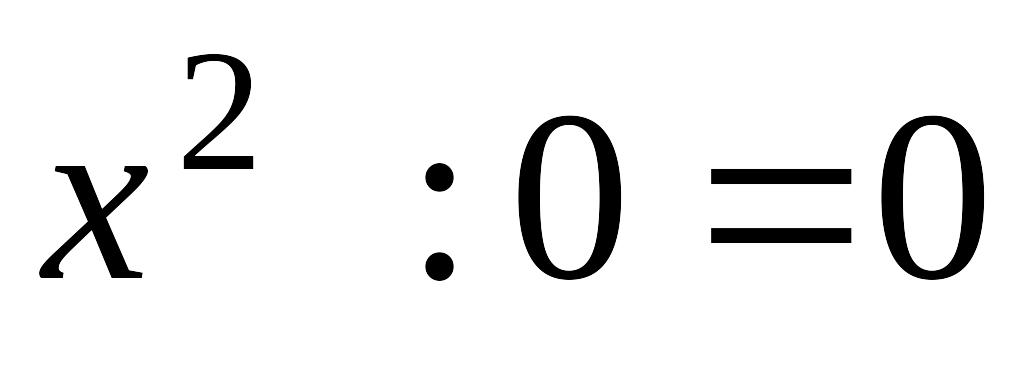
1

Т.о., . Общее решение .

(♠♠) , где - полином от степени (который, в частности, может быть константой, не равной нулю); - вещественное число.

Если число не является кратным корнем, то следует искать

в виде

,

где - полином той же степени с неопределенными коэффициентами.

Если же число является корнем характеристического уравнения кратности , то следует искать в виде

.

П. 9.13 .

Начальные данные: при .

Число не является корнем характеристического уравнения ,

. Общее решение однородного уравнения . Частное решение ищем в виде .

0
-2
1

Решая уравнения, находим . Т.о., .

Общее решение . Решаем задачу Коши.

. Имеем

. Решение, удовлетворяющее заданным начальным условиям, имеет следующий вид: .

П. 9.14

Число является простым корнем характеристического уравнения , . Общее решение однородного уравнения . Частное решение ищем в виде .

-1
0
1

; общее решение .

П. 9.15

Число является двукратным корнем характеристического уравнения , . Общее решение однородного уравнения . Частное решение ищем в виде .

1
-2
1

Т.о., . Общее решение .

(♠♠♠) , где - полиномы от (которые, в частности, могут быть константами и один из них может быть равным нулю); - вещественные числа.

Пусть - наибольшая из степеней полиномов .

Если число не является корнем характеристического уравнения, то следует искать в виде

,

где - полиномы степени с неопределенными коэффициентами.

Если число является корнем кратности , то следует искать в виде

.

П. 9.16

Корни характеристического уравнения . Общее решение однородного уравнения . Т.к.., ; число не является корнем характеристического уравнения , то частное решение ищем в виде .

-1
0
1

Значит, ; oбщее решение .

П. 9.17

Корни характеристического уравнения . Общее решение однородного уравнения . Т.к.., и число не является корнем характеристического уравнения , то частное решение ищем в виде .

-1
0
1

Решая уравнения, находим ; .

Oбщее решение .

П. 9.18

Корни характеристического уравнения . Общее решение од-нородного уравнения . Т.к.., ; и число не является корнем характеристического уравнения , то частное решение ищем в виде .

В данном случае пользоваться обычной схемой неудобно. Вначале находим производные .

Теперь следуем привычной схеме.

1
1

Т.о., .

Общее решение .

П. 9.19

Корни характеристического уравнения . Общее решение однородного уравнения .

Т.к.., и число является корнем харак-теристического уравнения , то частное решение ищем в виде :

Находим производные .

4
1

Т.о., ; общее решение .

П. 9.20 .

Найти вид частного решения.

Корни характеристического уравнения

.

Т.к.., и число является двукратным

корнем характеристического уравнения , то частное решение имеет вид :

(♠♠♠♠) ,

где - функции стандартного вида.

В этом случае ,

где - частное решение, отвечающее функции .

П. 9.21

Корни характеристического уравнения . Общее решение однородного уравнения .

Т.к.. для функции и число является корнем характеристического уравнения , то частное решение ; функции отвечает .

Итак, .

Далее, поступаем по рецепту:

1
0
1

Итак, . Общее решение .

Иногда правая часть уравнения не имеет стандартного вида, но с помощью преобразований может быть приведена к стандартному виду.

П. 9.22

Правя часть не имеет стандартного вида. Однако, т.к. , то

. Теперь правая часть имеет стандартный вид.

Корни характеристического уравнения . Общее решение однородного уравнения .

Т.к.. для функции и число является корнем характеристического уравнения , то частное решение ; функции отвечает .

Итак, .

4
0
1

Т.о., . Общее решение .

П. 9.23 . Найти вид частного решения.

Корни характеристического уравнения .

Т.к. , то .

3°. Метод вариации произвольных постоянных. Метод пригоден для линейных уравнений (с постоянными и произвольными коэффициентами), если известна фундаментальная система соответствующего однородного уравнения. Общее решение в этом случае можно найти для правой части произвольного вида (необязательно стандартного).

Суть метода (метода Лагранжа) состоит в том, что общее решение ищется в виде

,

где - непрерывно дифференцируемые функции от x;

- фундаментальная система решений соответствующего однород-

ного уравнения; - порядок уравнения.

Функции определяются из системы:

где - правая часть заданного уравнения.

П. 9.24 .

Корни характеристического уравнения . Фундаментальная система решений: . Общее решение ищем в виде:

. Записываем систему:

, .

Интегрируя, находим :

,

где - постоянные интегрирования. Общее решение:

.

П. 9.25

Корни характеристического уравнения . Фундаментальная система решений: . Общее решение ищем в виде:

. Записываем систему:

,

= .

.

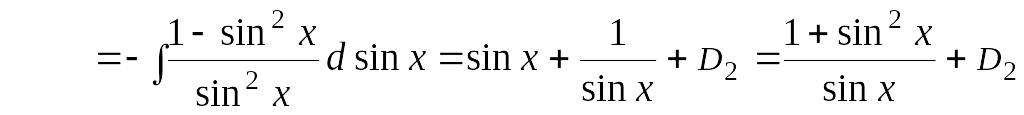Общее решение .

П. 9.26 . Фундаментальная система решений задана :

. Общее решение ищем в виде:

. Записываем систему:

, .

,

. .

Общее решение

.