5 Задание 5. Обработка экспериментальных данных при изучении зависимостей

1. Условие задания

При многократных совместных измерениях величин X и Y получено по 20 (n) пар результатов измерений. Эти результаты после внесения поправок представлены в таблице 4. Определить уравнение регрессии Y по X: Y = f (X).

5.2 Исходные данные

Таблица 5.1- Исходные данные

I	1	2	3	4	5	6	7
X,Y	1:10	1:10	2:21	3:32	4:42	5:49	6:58
I	8	9	10	11	12	13	14
X,Y	7:69	8:77	9:87	10:96	11:110	21:205	31:312
I	15	16	17	18	19	20
X,Y	41:405	51:505	61:602	71:696	81:795	91:880

2. Расчет

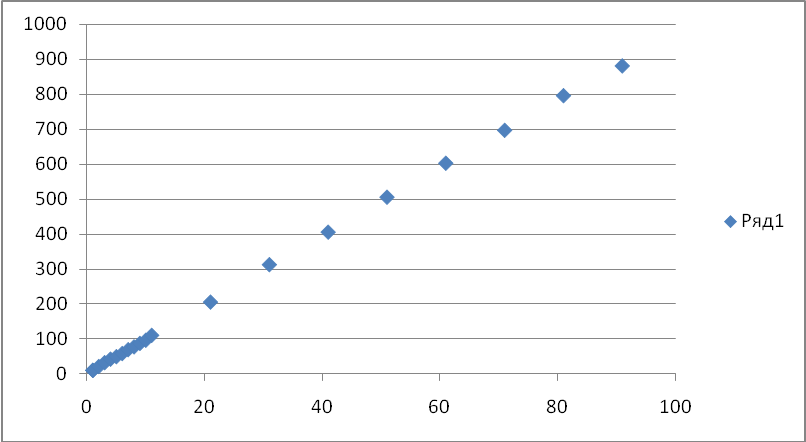
График 5,1- Эксперементальные данные

В качестве регрессии будем использовать прямую вида:

(5.1)

Параметры прямой определим по методу наименьших квадратов:

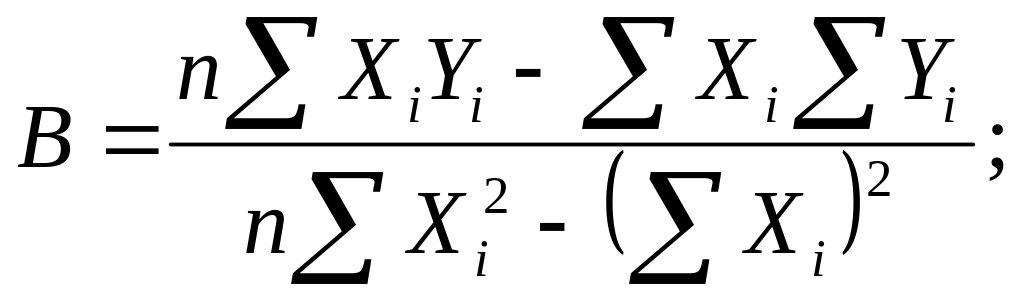(5.2)

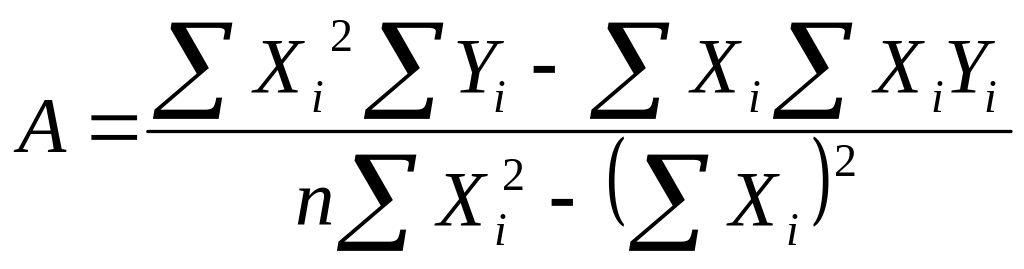(5.3)

B=9,77

A=1,37

Получаем:

Y=1,37+9,77*X

Далее проверяем правильность выбора вида уравнения регрессии. Для этого следует применить критерии серий и инверсий.

Рассчитываем отклонение экспериментальных значений от соответствующих расчетных значений, рассчитанных для того же аргумента:

Таблица 5.2- полученные значения

i	1	2	3	4	5	6	7
	-1.14	-1.14	0.08	1.31	1.53	-1.24	-2.01
i	8	9	10	11	12	13	14
	-0.79	-2.56	-2.34	-3.11	1.12	-1.62	7.64
i	15	16	17	18	19	20
	2.9	5.16	4.42	0.68	1.94	-10.8

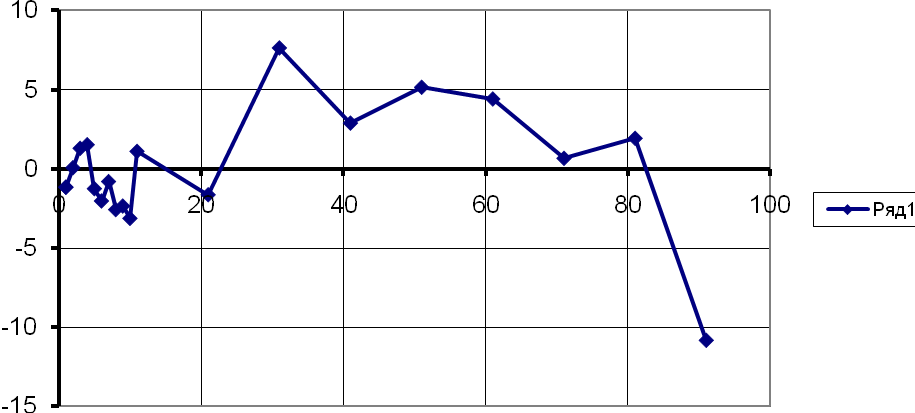
График 5.2 – Зависимость значений от X.

Критерий серий: расчитываем число серий в полученной последовательности: N=7

Задавшись доверительной вероятностью p=0,95 (a=1-p), для n=20 определяем по таблице допустимые границы N_1-0,5 и N_0,5;

N_1-0,5 =6

N_0,5=15

Критерий выполняется.

Критерий инверсий:

Расчитываем число инверсий А в полученной последовательности :

А = 7+8+9+9+6+4+5+2+1+2+6+3+4+3+1+1=71

Задавшись доверительной вероятностью p=0,95 (a=1-p) для n=20

Определяем по таблице допустимые границы A_1-0,5 и A_0,5;

A_1-0,5=69

A_0,5=120

Оба неравенства выполняются N_1-0,5 N_0,5 и A_1-0,5 A_0,5. Поэтому можно считать, что рассчитанное уравнение регрессии достоверно описывает эксперементально исследуемую зависимость.