Задание 4. Функциональные преобразования результатов измерений

(косвенные измерения)

Условие задания:

При многократных измерениях независимых величин X и Y получено по 12 ( ) результатов измерений в каждой. Эти результаты после внесения поправок представлены в таблице 4.1. Определить результат вычисления .

Таблица 4.1 – Исходные данные:

Х ЭДС, мВ	485	484	486	482	483	484	484	481	485	485	485	492
Y Cопротивление, Ом	484	481	480	481	484	485	485	484	483	483	485	492
Z=X/(Y+10) Cила тока

Решение

Произведем обработку данных при функциональном преобразовании результатов.

4.1 Обработка результатов величины X

Алгоритм проведения многократного измерения

Определяем точечные оценки результата измерения

Среднее арифметическое определяется по формуле:

,

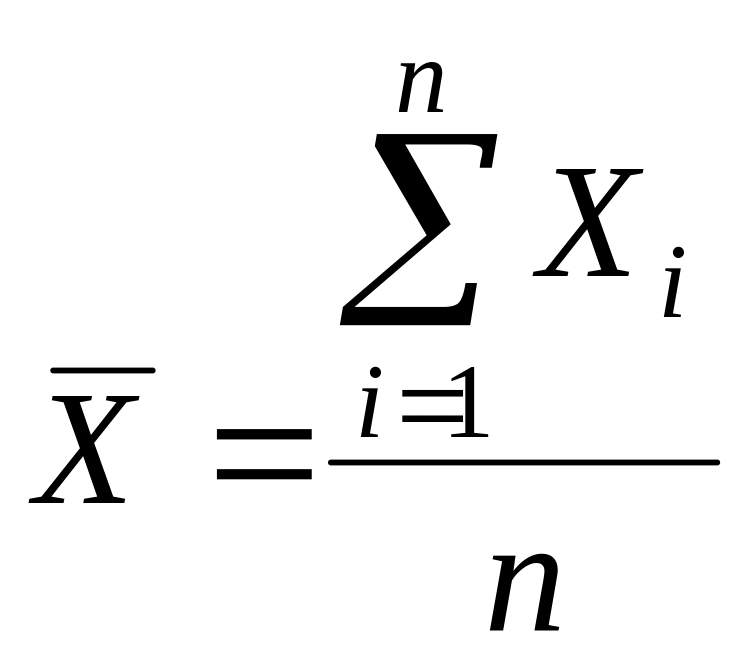где X_i – измеряемая величина;

n – число измерений, n = 12.

=484,67 мВ

Среднее квадратическое отклонение результата измерения:

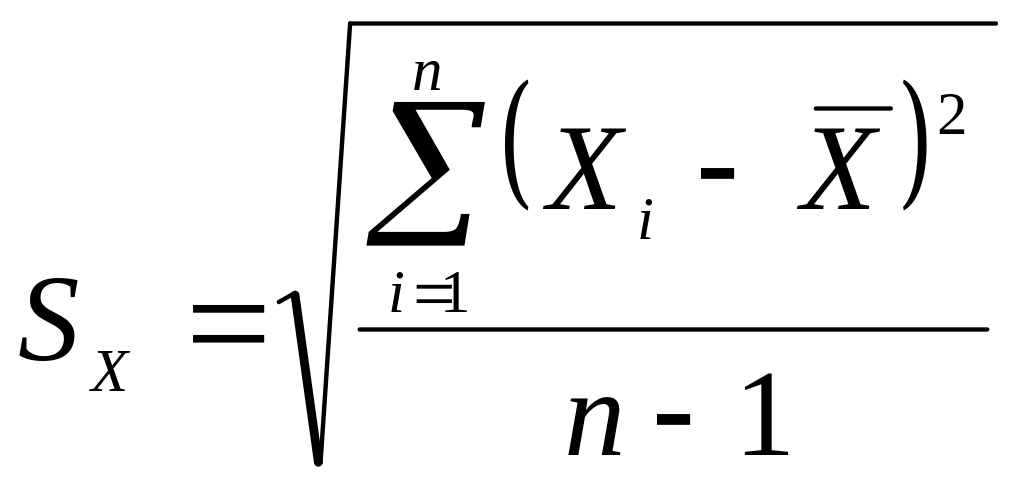
S_X = 2,71 мВ

Обнаруживаем и исключаем ошибки:

Вычисляем наибольшее по абсолютному значению нормированное отклонение:

,

 = 3,701

По таблице П6 [4] с доверительной вероятностью Р=0,95 с учетом q = 1–Р находим _ТАБ=2,387

Так как  > _ТАБ, то данный результат измерений Q = 492 ошибочный, он отбрасывается и повторяются вычисления.

=484,0 мВ

S_X = 1,48 мВ

 = 2,02

_ТАБ=2,064

Условие  < _ТАБ выполняется. Больше ошибочных результатов нет.

Проверка гипотезы о нормальности распределения оставшихся результатов измерений.

Применим критерий 1.

Вычисляем отношение

Задавшись доверительной вероятностью P₁=0,98, с учетом q₁ = 1– P₁ определяем по таблице П7 [4] квантили распределения:

=0,6675 =0,9359

<d<

0,6675 < 0,7628 < 0,9359

Так как <d< , то гипотеза о нормальном законе распределения вероятности результата измерения первой серии согласуется с экспериментальными данными.

Применим критерий 2.

Задавшись доверительной вероятностью P₂=0,98 и для уровня значимости q₂=1–P₂ с учетом n = 11 по таблице П8 [4] определяем значения m=1 и Р*=0,98

Для вероятности из таблицы 1.1.2.6.2 [3] для интегральной функции нормированного нормального распределения (t) определяем значение t=2,33

Рассчитаем Е

Определим разность . Данные результаты представлены в таблице 4.2.

Таблица 4.2

Номер измерения	1	2	3	4	5	6	7	8	9	10	11
разность	1	0	0	1	0	0	1	1	1	2	1

Так как ни одна из разностей не превосходит Е, то гипотеза о нормальном законе распределении вероятности результата измерения согласуется с экспериментальными данными. Закон распределения оставшихся результатов первой серии можно признать нормальным с вероятностью .

.