МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФГБОУ ВПО «ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ –

УЧЕБНО-НАУЧНО-ПРОИЗВОДСТВЕННЫЙ КОМПЛЕКС»

Кафедра «Приборостроение, метрология и сертификация»

КУРСОВАЯ РАБОТА

по дисциплине «Метрология, стандартизация, и сертификация»

Студент Сиротин

Факультет

Шифр 79

Группа 31-УК

Проверил преподаватель Марков В.В.

Работа защищена с оценкой _____________

Орел 2013 г.

Содержание

стр.

Задание 1. Однократное измерение 3

Задание 2. Многократное измерение 5

Задание 3. Обработка результатов нескольких серий измерений 9

Задание 4 Функциональные преобразования результатов измерений

(косвенные измерения) 16

Задание 5. Обработка экспериментальных данных при изучении

Зависимостей 22

Список использованных источников 26

Задание 1 Однократное измерение

Условие:

При однократном измерении физической величины получено показание средств измерения X=10. определить, чему равно значение измеряемой величины, если экспериментатор обладает априорной информацией о средстве измерении и условиях выполнения измерений: класс точности средства измерения.

Закон распределения вероятности результата измерения нормальный,

оценка среднего квадратического отклонения Sx=0,1

доверительная вероятность 0,9

мультипликативная поправка 0,95.

Решение:

1) Анализ априорной информации

Закон распределения вероятности результата измерения нормальный

оценка среднего квадратического отклонения Sx=0,1

доверительная вероятность 0,9

Известно значение мультипликативой поправки QМ =0,95

2) Получение единственного отсчета

х= 10

3) Получение единственного показания прибора

X=10

4) Принятие решения о методике нахождения доверительного интервала.

Закон распределения - нормальный, доверительный интервал определяется следующим образом

,

,

,

E=t*Sx,

Где t=1,64,

Е=1,64*0,1=0,164,

Q₁=10-0,164=9,836

Q₂=10+0,164=10,164

5) Внесение поправки и уточнение пределов, в которых находится значение измеряемой величины

Результат измерения:

Задание 2. Многократное измерение

Условие:

При многократном измерении одной и той же физической величины, получена серия из 24 результатов измерений , . Эти результаты после внесения поправок представлены ниже. Определить результат измерения.

Исходные данные:

Таблица 2.1

№ измерения	Результат измерения
1	485
2	484
3	486
4	482
5	483
6	484
7	484
8	481
9	485
10	485
11	485
12	492
13	484
14	481
15	480
16	481
17	484
18	485
19	485
20	484
21	483
22	483
23	485
24	492

Решение

Алгоритм проведения многократного измерения

1. Определяем точечные оценки результата измерения

Среднее арифметическое определяется по формуле:

,

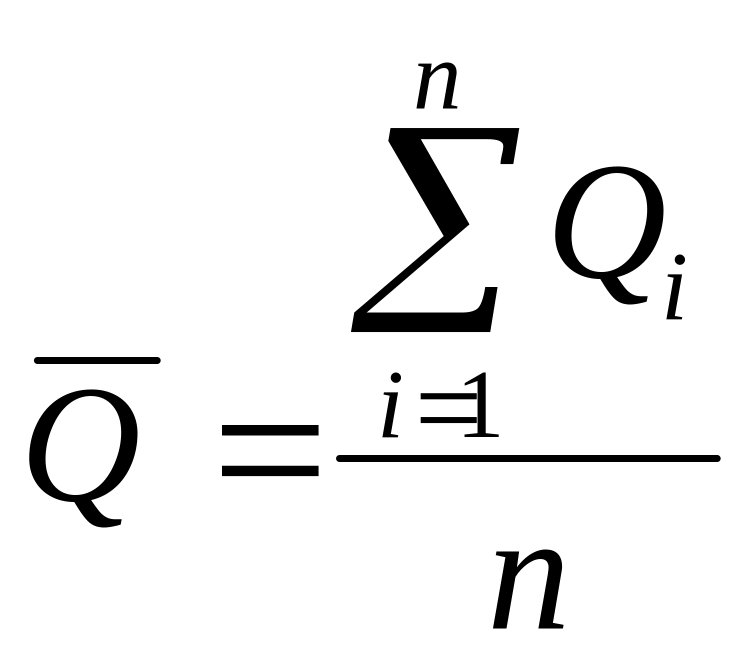где Q_i – измеряемая величина;

n – число измерений.

=484,292

Среднее квадратическое отклонение результата измерения:

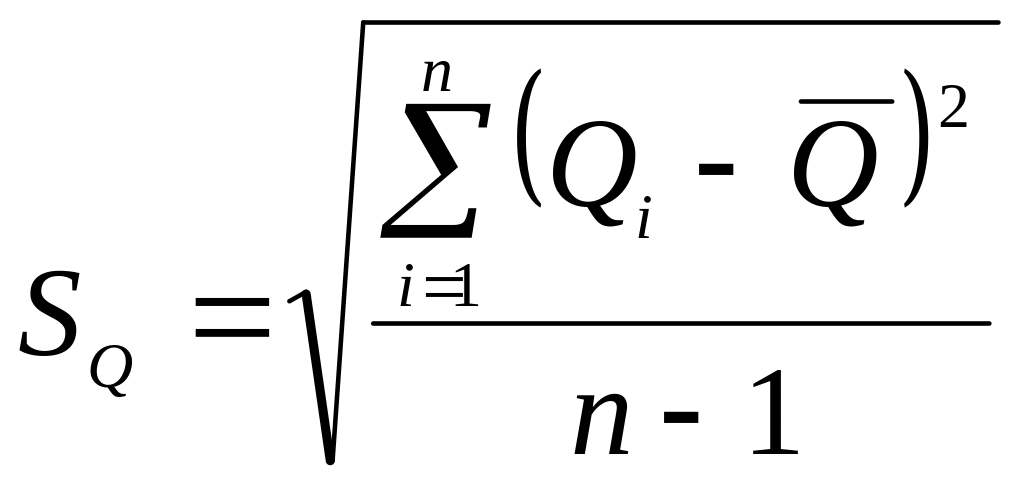
S_Q = 2,854

2. Обнаруживаем и исключаем ошибки с помощью  критерия:

Вычисляем наибольшее по абсолютному значению нормированное отклонение:

,

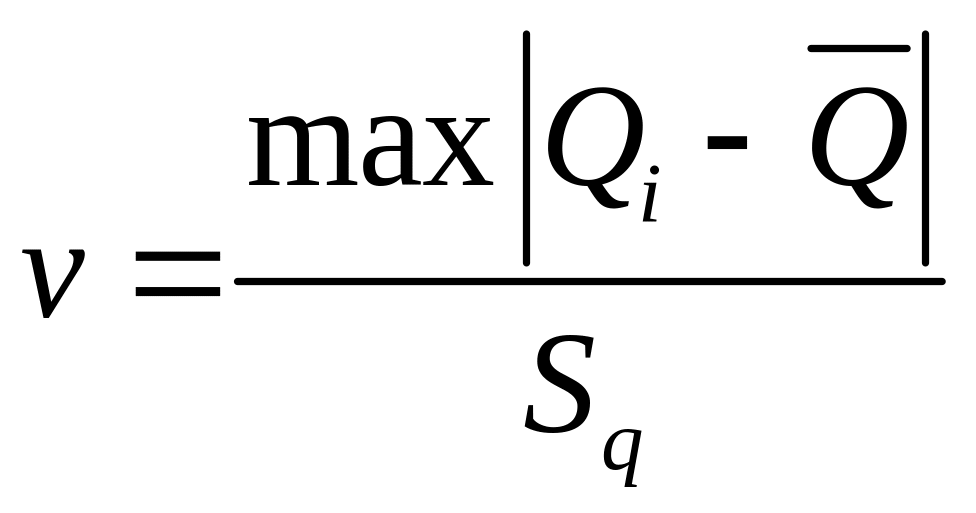Для результата измерения, равного 492  = 2,771

По таблице П6 [4] с доверительной вероятностью Р=0,95 с учетом q = 1–Р находим _ТАБ=2,701

Так как  > _ТАБ, то данный результат измерений Q = 492 ошибочный, он отбрасывается и повторяются вычисления.

=483,591

S_Q = 1,583

 = 2,269

_ТАБ=2,688

Условие  < _ТАБ выполняется. Больше ошибочных результатов нет.

3. Проверка гипотезы о нормальности распределения оставшихся результатов измерений.

Применим критерий 1.

Вычисляем отношение

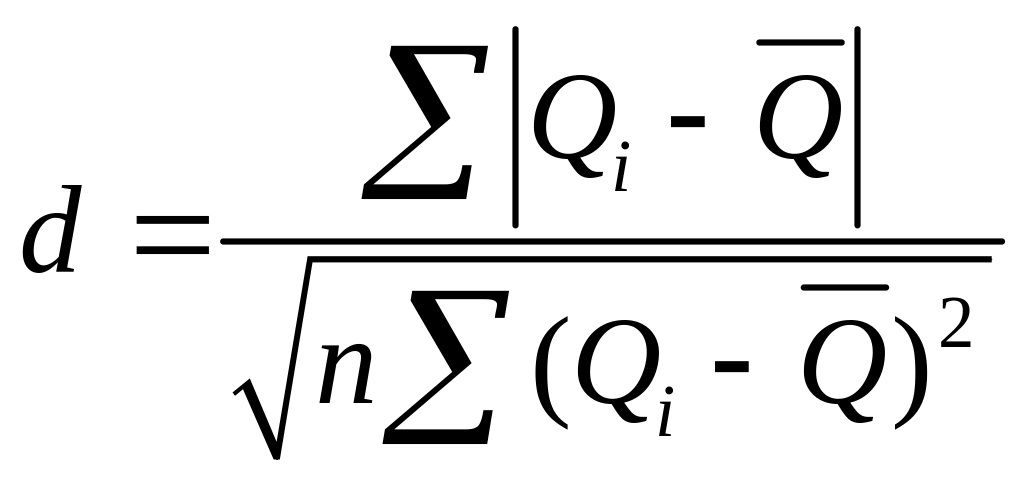
Задавшись доверительной вероятностью P₁=0,98, с учетом q₁ = 1– P₁ определяем по таблице П7 [4] квантили распределения:

=0,6950 =0,9001

<d<

0,6950 < 0,829 < 0,9001

Так как <d< , то гипотеза о нормальном законе распределения вероятности результата измерения согласуется с экспериментальными данными.

Применим критерий 2.

Задавшись доверительной вероятностью P₂=0,98 и для уровня значимости q₂=1–P₂ с учетом n = 22 по таблице П8 [4] определяем значения m=2 и Р*=0,97

Для вероятности Р*=0,97 из таблицы 1.1.2.6.2 [3] для интегральной функции нормированного нормального распределения (t) определяем значение t=2,17

Рассчитаем Е

Определим разность . Данные результаты представлены в таблице 2.2.

Таблица 2.2

Номер измерения	1	2	3	4	5	6	7	8	9	10	11
разность	1,41	0,41	2,41	1,59	0,59	0,41	0,41	2,59	1,41	1,41	1,41

Номер измерения	12	13	14	15	16	17	18	19	20	21	22
разность	0,41	2,59	3,59	2,59	0,41	1,41	1,41	0,41	0,59	0,59	1,41

Так как всего одна разность превосходит Е ( =3,59 для n=14), то гипотеза о нормальном законе распределении вероятности результата измерения согласуется с экспериментальными данными, закон можно признать нормальным с вероятностью .

.

4. Определение среднеквадратического отклонения среднего арифметического:

5. Определение доверительного интервала

,

где t – коэффициент Стьюдента.

t выбирается из таблицы 1.1.2.8 [3], при этом m = n – 1,  = P

t = 2,086

6. Результат измерения , n , P

Ответ: n = 22 P = 0,95