Приоритет логических операций

При вычислении значения логического выражения логические операции вычисляются в определенном порядке, согласно их приоритету:

• инверсия;

• действия в скобках;

• конъюнкция;

• дизъюнкция;

• импликация;

• эквиваленция.

Закрепление:

1. Определить форму сложного высказывания.

1) Если вы пользуетесь последними версиями антивирусных программ или регулярно сохраняете свои файлы на дискетах, то снижается вероятность потери данных.

А = Вы пользуетесь последними версиями антивирусных программ;

В = Вы регулярно сохраняете свои файлы на дискетах;

С = Снижается вероятность потери данных.

_{2) Идет дождь, а у меня нет зонта.}

_{А = Идет дождь.}

_{В = У меня есть зонт.}

3) Когда живется весело, то и работа спорится.

А = Живется весело.

В = Работа спорится.

_{4) Идет налево – песнь заводит, направо – сказку говорит.}

А = Идет налево.

В = Идет направо.

С = Песнь заводит.

D = Сказку говорит.

2. Определите истинность составного высказывания: 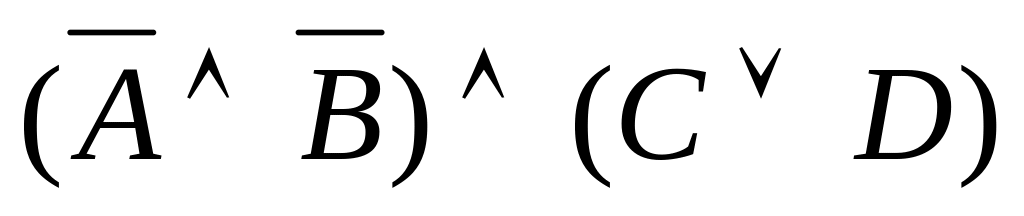, состоящего из простых высказываний:

А = {Принтер – устройство вывода информации},

В = {Процессор – устройство хранения информации},

С = {Монитор – устройство вывода информации},

D = {Клавиатура – устройство обработки информации}.

 

Сначала на основании знания устройства компьютера устанавливаем истинность простых высказываний: А = , В = , С = , D = .

Определим теперь истинность составного высказывания, используя таблицы истинности логических операций:

Составное высказывание _____________________

Домашнее задание:

1. Определить форму сложного высказывания.

1) Ваш приезд не является ни необходимым, ни желательным.

А = Ваш приезд необходим.

В = Ваш приезд желателен.

2) Поиски врага длились уже три часа, но результатов не было, притаившийся враг ничем себя не выдавал.

А = Поиски врага длились три часа.

В = Врага нашли (результат есть).

С = Враг себя выдал.

3) Вчера было пасмурно, а сегодня ярко светит солнце.

А = Вчера было пасмурно.

В = Сегодня ярко светит солнце.

4) И добродетель стать пороком может, когда ее неправильно приложат.

А = Добродетель неправильно приложат.

В = Добродетель стать пороком может.

2. По форме высказывания и выраженным на естественном языке составляющим его простым высказываниям получить фразу на естественном языке.

А = Некто является врачом.

В = Больной поговорил с врачом.

С = Больному стало легче.

____________________________________________________________________________________________________________________________________________________________________________

3. Даны простые высказывания:

А = {Принтер – устройство ввода информации},

В = {Процессор – устройство обработки информации},

С = {Монитор – устройство хранения информации},

D = {Клавиатура – устройство ввода информации}.

Определите истинность составных высказываний:

а) (АВ)  (C  D); б) (АВ)    (C  D);

в) (А  В)    (C  D); г) .

Тема: Построение таблиц истинности сложных высказываний

Тест: Логические высказывания. В-1

1. Признаками понятия обладает высказывание:

   1. «Грачи прилетели»;

   2. «Низко летающие птицы»;

   3. «Птицы летают низко»;

   4. «Грачи весну принесли».

2. «Наступил сентябрь, и начался учебный год» - это суждение:

   1. простое и истинное;

   2. сложное и истинное;

   3. простое и ложное;

   4. сложное и ложное.

3. «Все растенья съедобны» - это суждение следующего типа:

   1. простое и истинное;

   2. сложное и истинное;

   3. простое и ложное;

   4. сложное и ложное.

4. Выбрать пример, не являющийся высказыванием:

   1. «Не можете ли вы передать соль?»;

   2. «Гоголь писал «Мертвые души» в Риме»;

   3. «Рукописи не говорят»;

   4. «Некоторые лекарства опаснее самих болезней».

5. Из предложенных посылок:

«Память компьютера делится на внутреннюю и внешнюю»;

«Данная память не является внешней» вытекает заключение:

1. «Данная память не является внутренней»;

2. «Данная память является внутренней»;

3. «Данная память является внешней»;

4. «Данная память не делится».

1. Отрицанием высказывания

«Для каждого из нас учить второй иностранный язык легче, чем первый»

является высказывание:

1. «Не для каждого из нас учить второй иностранный язык легче, чем первый»;

2. «Для каждого из нас не учить второй иностранный язык легче, чем первый»;

3. «Неверно, что для каждого из нас учить второй иностранный язык легче, чем первый»;

4. «Неверно, что для каждого из нас учить второй иностранный язык не легче, чем первый».

1. Знаком ^ в логике обозначается следующая операция:

   1. инверсия; 3) дизъюнкция;

   2. конъюнкция; 4) импликация.

2. Знаком =>в логике обозначается следующая операция:

   1. конъюнкция; 3) импликация;

   2. дизъюнкция; 4) эквиваленция.

3. Логическая операция с использованием ключевых слов «Если . . . то . . .», называется:

   1. конъюнкцией; 3) импликацией;

   2. дизъюнкцией; 4) эквиваленцией.

4. Формулой логического высказывания

«Если у меня будет свободное время и не будет дождя, то я не буду писать сочинение, а пойду на дискотеку» является:

1. 3)

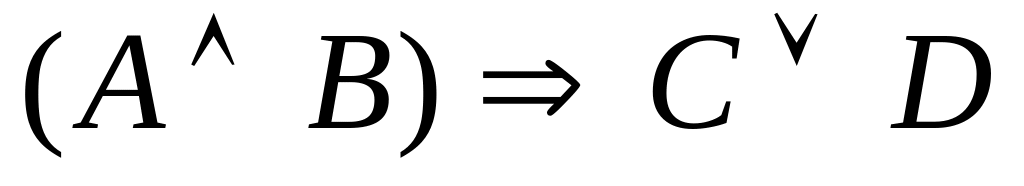2. ; 4) .

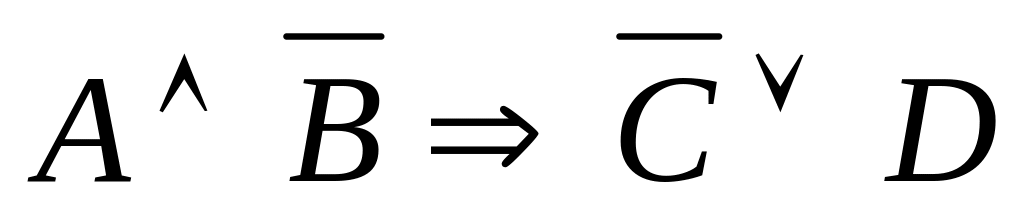Ответы:

Тест: Логические высказывания. В-2

1. Признаками понятия обладает высказывание:

   1. «Собеседник говорил громко»;

   2. «Громко говорящий собеседник»;

   3. «Говорите громко!»;

   4. «Громкий голос раздражает».

2. «Если прошел снег, то на улице лето» - это суждение:

   1. простое и истинное;

   2. сложное и истинное;

   3. простое и ложное;

   4. сложное и ложное.

3. «Все ученики любят физику» - это суждение следующего типа:

   1. простое и истинное;

   2. сложное и истинное;

   3. простое и ложное;

   4. сложное и ложное.

4. Выбрать пример, не являющийся высказыванием:

   1. «Никакая причина не извиняет невежливость»;

   2. «Если совет разумен, то следует выполнить его»;

   3. «Обязательно стань отличником»;

   4. «Спортом заниматься полезно».

5. Из предложенных посылок:

«Все улетающие на юг птицы, называются перелетными»;

«Все грачи зимой улетают на юг» вытекает заключение:

1. «Все перелетные птицы - грачи»;

2. «Все птицы зимой живут на юге»;

3. «Грачи – перелетные птицы»;

4. «Некоторые грачи не живут зимой на юге».

1. Отрицанием высказывания

«Некоторые школьники предпочитают изучать китайский язык»

является высказывание:

1. «Некоторые школьники не предпочитают изучать китайский язык»;

2. «Некоторые школьники предпочитают изучать не китайский язык»;

3. «Неверно, что некоторые школьники предпочитают изучать китайский язык»;

4. «Неверно, что школьники предпочитают не изучать китайский язык».

1. Знаком в логике обозначается следующая операция:

   1. инверсия; 3) дизъюнкция;

   2. конъюнкция; 4) импликация.

2. Знаком в логике обозначается следующая операция:

   1. конъюнкция; 3) импликация;

   2. дизъюнкция; 4) эквиваленция.

3. Логическая операция с использованием ключевых слов «тогда и только тогда, когда . . .», называется:

   1. конъюнкцией; 3) импликацией;

   2. дизъюнкцией; 4) эквиваленцией.

4. Формулой логического высказывания

«Без Вас хочу сказать Вам много,

При Вас я слушать Вас хочу» является:

1. 3)

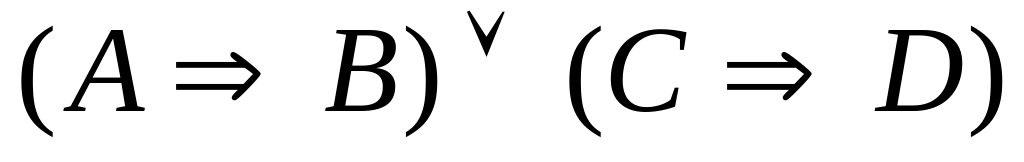2. ; 4) .

Ответы:

Актуализация опорных знаний.

1) Дана формула: .

Определить порядок вычисления.

2) Дана формула: .

Определить порядок вычисления.

3) Найдите значения логических выражений:

       а) (11)(10)=1;

       б) ((10)1)1=1;

       в) (01)(10)=1;

       г) (0 1) 1=0;

       д) 1 (1 1) 1=1;

       е) ((10) (1 1)) (01)=1;

       ж) ((1 0)(1 0))1=1

       з) ((1 1)0) 0 1=0;

       и) ((0 0)0) (11)=0.

Объяснение нового материала.

Таблицу, показывающую, какие значения принимает составное высказывание при всех сочетаниях (наборах) значений входящих в него простых высказываний, называют таблицей истинности составного высказывания.

Составные высказывания в алгебре логики записываются с помощью логических выражений. Для любого логического выражения достаточно просто построить таблицу истинности.

Алгоритм построения таблицы истинности:

1)       подсчитать количество переменных n в логическом выражении;

2)       определить число строк в таблице, которое равно m = 2ⁿ;

3)       подсчитать количество логических операций в логическом выражении и определить количество столбцов в таблице, которое равно количеству переменных плюс количество операций;

4)       ввести названия столбцов таблицы в соответствии с последовательностью выполнения логических операций с учетом скобок и приоритетов;

5)       заполнить столбцы входных переменных наборами значений;

6)       провести заполнение таблицы истинности по столбцам.

Например: Для формулы A (B  ) построить таблицу истинности.

1. Количество логических переменных 3, следовательно, количество строк в таблице истинности должно быть 2³ = 8.

2. Количество логических операций в формуле 5, следовательно количество столбцов в таблице истинности должно быть 3 + 5 = 8.

A	B	C				B  ( )	A (B  )
0	0	0	1	1	1	1	0
0	0	1	1	0	0	0	0
0	1	0	0	1	0	1	0
1	0	0	1	1	1	1	1
0	1	1	0	0	0	1	0
1	0	1	1	0	0	0	0
1	1	0	0	1	0	1	1
1	1	1	0	0	0	1	1

Если высказывание истинно при всех значениях входящих в него переменных, то такое высказывание называется тождественно истинным или тавтологией.

Если высказывание ложно при всех значениях входящих в него переменных, то такое высказывание называется тождественно ложным.

Если значения сложных высказываний совпадают на всех возможных наборах значений входящих в них переменных, то такие высказывания называются равносильными, тождественными, эквивалентными.

Закрепление.

Построить таблицу истинности для следующих формул:

а)

A	B	C
0	0	0
0	0	1
0	1	0
1	0	0
0	1	1
1	0	1
1	1	0
1	1	1

б)

A	B	C
0	0	0
0	0	1
0	1	0
1	0	0
0	1	1
1	0	1
1	1	0
1	1	1

в)

A	B	C					А 
0	0	0	1
0	0	1	1
0	1	0	0
1	0	0	1
0	1	1	0
1	0	1	1
1	1	0	0
1	1	1	0