8.2 Решение задачи о максимальном потоке. Алгоритм Фалкерсона

Пусть дана некоторая сеть. Разобьем множество вершин сети на два непересекающихся подмножества А и В так, чтобы исток I попал в подмножество А, а сток S – в подмножество В. В этом случае говорят, что на сети произведен разрез, отделяющий исток I от стока S. В результате произведенного разбиения вершин появятся ребра (i, j), конечные точки которых окажутся в разных подмножествах. Совокупность ребер (i, j), начальные точки которых принадлежат подмножеству А, а конечные – подмножеству В, называют разрезом сети и обозначают А/В.

На рисунке 8.1 изображена сеть, на которой около каждого ребра указана его пропускная способность в обоих направлениях (в скобках). Кроме этого, на рисунке 8.1 сети произведены два разреза: I и II. При разрезе I вершины сети оказались разбиты на два подмножества А={1} и В={2, 3, 4, 5}, а ребрами, образующими разрез стали (1, 2), (1, 3) и (1, 4). При разрезе II А={1, 2}; В={3,4,5}, а образуют разрез ребра (1, 3), (14) ), (2, 3) и (2, 5).

Введем важные определения.

Величина:

представляет собой сумму пропускных способностей r_ij всех ребер разреза, называется пропускной способностью разреза.

Пусть на сети задан поток X={x_ij} и произведен разрез А/В. Величина

Представляет собой сумму потоков x_ij по всем ребрам разреза, называется потоком через разрез.

Если на сети задан поток X={x_ij} и произведен разрез А/В, то хотя бы одно ребро любого полного пути, ведущего из истока I в сток S будет обязательно принадлежать разрезу А/В. При этом величина потока по любому полному пути не превышает пропускную способность каждого его ребра, а потому величина X суммарного потока, устремленного из истока I в сток S, не может превысить пропускную способность любого разреза сети:

Оказывается, если удается построить на сети поток X={x_ij}, величина которого равна пропускной способности некоторого разреза А/В, то этот поток будет максимальным, а разрез А/В обладает минимальной пропускной способностью.

Справедлива следующая теорема Форда – Фалкерсона, которая имеет важное прикладное значение. На любой сети максимальная величина потока из истока I в сток S равна минимальной пропускной способности разреза, отделяющего I от S. Доказательство приведено, например, в [2].

Впервые был предложен в 1956г. До этого времени задача решалась с помощью методов линейного программирования, что было крайне не эффективно.

Алгоритм начинает свою работу с нулевого потока и на каждой своей итерации увеличивает поток в сети. На каждом шаге находится увеличивающая величину потока цепь. Поток увеличивается вдоль дуг этой цепи, пока она не станет насыщенной.

Увеличивающей цепью является цепь из истока в сток, все дуги которой допустимы. Дугу из вершины i в вершину j назовем допустимой, если выполняется одно из следующих условий:

1)      x_ij<r_ij и дуга согласованна;

2)      r_ij>0 и дуга несогласованна.

По увеличивающей цепи можно пустить поток величины Q, где Q = min{q_i, 1 ≤ i ≤ l} и q_i = {x_ij – r_ij, если дуга согласованна, x_ij, если дуга не согласованна}. Для того, чтобы увеличить величину потока сети на Q,  необходимо увеличить на Q поток на каждой согласованной дуге цепи и уменьшить на каждой несогласованной.

В своей работе Форд и Фалкерсон доказали, что поток в сети, для которой нельзя построить увеличивающую цепь, является максимальным.

Для нахождения увеличивающей цепи ими был предложен «Метод расстановки пометок» [2]. Процесс расстановки меток начинается в источнике сети и заканчивается в ее стоке. Как только сток оказался помеченным, мы можем говорить о существовании увеличивающей цепи из истока в сток. Метка, «наносимая» на вершины сети, содержит необходимый минимум информации, достаточный для того, чтобы восстановить эту цепь и определить величину, на которую можно изменить поток в ней. Вершина сети может находиться в одном из 3-х состояний: «непомеченная», «помеченная» и «просмотренная».

Этап 1. Расстановка меток

Все вершины получают статус непомеченных.

Процедура  расстановки меток.

Возьмем произвольный помеченный, но не просмотренный узел z. Пусть он имеет пометку [i, +, e(z)], где i – вершина из которой был помечен z; флаг, показывающий, что дуга (i, z) согласованна; e – величина потока, который можно пропустить по этой дуге. Рассмотрим все непомеченные смежные вершины y, такие что дуга (z, y) согласованна. Пометим вершину y меткой [z, +, e(y)], где e(y) = min{e(z) , r_zy – x_zy}. Затем рассмотрим все непомеченные смежные вершины y, соединенные с ней несогласованной дугой. Пометим их меткой [z, -, e(y)], где e(y) = min{e(z), x_zy}. Теперь все рассмотренные узлы y имеют статус помеченных, а узел z - просмотренный.

Эта общая для всех узлов сети процедура. Пометим исток меткой [~, ~, ∞] и будем последовательно вызывать ее для всех смежных узлов, постепенно двигаясь по сети. Как только процедура будет вызвана для стока, будет получена увеличивающая цепь и следует перейти ко второму этапу. В противном случае процедура будет вызываться, пока все помеченные вершины не станут просмотренными, и если сток сети не был достигнут – увеличивающая цепь не может быть построена и по теореме Форда-Фалкерсона имеющийся поток сети является максимальным.

Этап 2. Изменение потока

Процедура изменения потока дуги.

Возьмем узел z.  Если он имеет метку [y, +, e], то увеличим поток по дуге (y, z) на e. Если он имеет метку [y, -, e], то уменьшим поток по дуге (y, z) на e. Если y не является источником, то вызовем процедуру для узла y.

Эта процедура, будучи вызвана для стока сети, позволяет пройти по найденной увеличивающей цепи к истоку, изменяя поток на ее дугах.

Алгоритм Форда-Фалкерсона гарантирует нахождение максимального потока только в сетях с целочисленными пропускными способностями. На практике «чистый» алгоритм Форда-Фалкерсона не применяется, т.к. оценка его производительности зависит от величины пропускных способностей дуг сети. Все дело в том, что в нем не дается каких либо правил выбора увеличивающей цепи.

Рассмотрим сеть на рисунке 8.2. Предположим, что реализован алгоритм, отдающий предпочтение увеличивающим цепям максимальной длины. В этом случае на первом шаге мы пустим дополнительный поток по цепи (1,2),(2,3),(3,4) (рисунок 8.3).

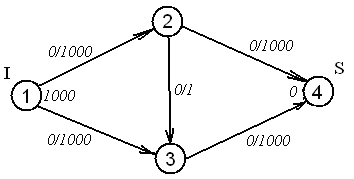
Рисунок 8.2 – Рассматриваемая сеть

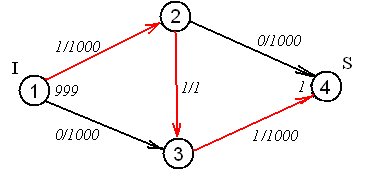
Рисунок 8.3 – Рассматриваемая сеть после первой итерации

На втором шаге выберем цепь (1,3),(3,2),(2,4). Так как дуга (3,2) несогласованна, величина пущенного по ней потока будет вычитаться из величины потока, полученного на предыдущем шаге. Мы получили сеть (рисунок 8.5) практически эквивалентную исходной.

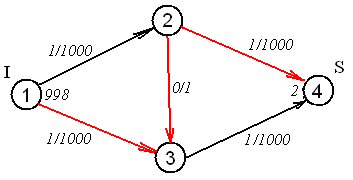
Рисунок 8.4 – Рассматриваемая сеть после второй итерации

Очевидно, что для нахождения максимального потока понадобиться 1000 итераций. В то время как, если бы мы на первом шаге выбрали цепь (1,2),(2,4), то результат был бы получен за одну итерацию. На практике, величина пропускных способностей часто зависит от единиц измерения, и может принимать огромные значения. Если же допустить иррациональные пропускные способности дуг, то можно привести пример невычислимой сети. Величина потока в такой сети не превысит даже четверти истинного значения.  Подобная неопределенность длилась не долго, уже вначале 70-х г. были предложены сразу 2 правила выбора увеличивающих цепей, которые существенно улучшают алгоритм Форда-Фалкерсона.

Наиболее известны алгоритмы Эдмондса-Карпа:

1) Алгоритм кратчайших увеличивающих цепей. Суть этого алгоритма сводится к тому, что все дуги имеют единичную длину. В качестве увеличивающей цепи выбирается цепь наименьшей длины, при этом не учитывается пропускная способность дуг этой цепи.

2) Алгоритм локально-максимального увеличения. Согласно этому методу, поток изменяется вдоль цепи с наибольшей пропускной способностью.

Мы остановимся на последнем, который изложен в [6].