Контрольные вопросы
Как открытую транспортную задачу свести к закрытой?
Какими методами можно найти начальное допустимое решение для транспортной задачи?
Каким образом при решении транспортной задачи методом потенциалов в текущей итерации находят вводимую в базис переменную?
Каким образом в транспортной задаче в текущей итерации находят исключаемую из базиса переменную?
Можно ли решить задачу о назначениях методом потенциалов?
Если при решении задачи о назначениях венгерским методом при вычеркивании нулей окажется, что вычеркнуты все строки и столбцы, что это означает?
Тема 7 Основы сетевого планирования
7.1 Основные понятия теории графов
Современное сетевое планирование начинается с разбиения программы работ на операции, далее определяются оценки продолжительности операций, а затем строится сетевая модель (график). Построение сетевой модели позволяет проанализировать все операции, входящие в проект, и внести улучшения в структуру модели до начала ее реализации.
Сетевая модель – графическое изображение плана выполнения комплекса работ, состоящего из нитей (работ) и узлов (событий), которые отражают логическую взаимосвязь всех операций. В основе сетевого моделирования лежит изображение планируемого комплекса работ в виде графа.
Граф – схема, состоящая из заданных точек (вершин), соединенных системой линий. Отрезки, соединяющие вершины, называются ребрами или дугами графа. Если указано, какая вершина является начальной, то отрезки называются дугами, а сам граф – ориентированным (орграфом). Если ориентация вершин не указана, то отрезки называются ребрами, а граф называется неориентированным.
Теория графов оперирует понятием пути, объединяющим последовательность взаимосвязанных ребер. Контур означает такой путь, у которого начальная вершина совпадает с конечной. Сетевой график – это ориентированный граф без контуров. В сетевом моделировании имеются два основных понятия – работа и событие.
Работа – это либо активный процесс, требующий затрат ресурсов, либо пассивный процесс (ожидание), приводящий к достижению намеченного результата.
Фиктивная работа – это связь между результатами работ (событиями), не требующая затрат времени и ресурсов.
Событие – это результат (промежуточный или конечный) выполнения одной или нескольких предшествующих работ.
Путь – это любая непрерывная последовательность (цепь) работ и событий.
Критический путь – это путь, имеющий наибольшую продолжительность по времени; он включает самые напряженные работы комплекса.
Работы, расположенные на критическом пути, называются критическими. Все остальные работы называются некритическими и обладают резервом времени, который позволяет передвигать сроки их выполнения, не влияя на общую продолжительность выполнения всего комплекса работ.
При построении сетевых моделей необходимо соблюдать следующие правила:
Сеть изображается слева направо, и каждое событие с большим порядковым номером изображается правее предыдущего. Общее направление стрелок, изображающих работы, также в основном должно расположено быть слева направо, при этом каждая работа должна выходить из события с меньшим номером и входить в событие с большим номером.
Два соседних события могут объединяться лишь одной работой. Для изображения параллельных работ вводятся промежуточное событие и фиктивная работа (рисунок 7.1).
Рисунок 7.1 Изображение на сетевом графике параллельных работ
В сети не должно быть тупиков, т.е. промежуточных событий, из которых не выходит ни одна работа (рисунок 7.2)
Рисунок 7.2 В сетевом графике нет промежуточных событий без продолжения
В сети не должно быть промежуточных событий, которым не предшествует хотя бы одна работа (рисунок 7.3).
Рисунок 7.3 В графике нет висячих событий
В сети не должно быть замкнутых контуров, состоящих из взаимосвязанных работ, создающих замкнутую сеть (рисунок 7.4).
Рисунок 7.4 Не должно быть путей типа k j s k
Для правильной нумерации событий поступают следующим образом: нумерация событий начинается с исходного события (в него не входит ни одна работа, таких бывает только одно событие), которому дается номер 1 (рисунок 7.5 а). Из исходного события 1 вычеркиваются все исходящие из него работы; на оставшейся сети вновь находят событие, в которое не входит ни одна работа. Этому событию дается номер 2 (рисунок 7.5 б). Затем вычеркивают работы, выходящие из работы 2, и вновь находят на оставшейся части сети событие, в которое не входит ни одна работа – ему присваивается номер 3 (рисунок 7.5 в), и так продолжается до завершающего события (рисунок 7.5 г).
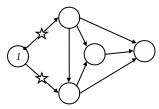
Рисунок 7.5 а) Рисунок 7.5 б)
Рисунок 7.5 г) Рисунок 7.5 д)
Построение сетевого графика начинается с составления списка работ, подлежащих выполнению. Их последовательность в списке произвольная, порядок нумерации осуществляется в соответствии с их последовательностью в списке. Перечень работ и событий тщательно продумывается и детализируется в зависимости от конкретных условий. Работы, включенные в список, характеризуются определенной продолжительностью, которая устанавливается на основании действующих нормативов или по аналогии с ранее выполнявшимися операциями. Такие временные оценки называются детерминированными (однозначными). Если нормативные данные временных оценок отсутствуют, то они определяются по экспертным оценкам специалистов и называются стохастическими (вероятностными).
После составления списка работ приступают к процедуре построения сетевого графа. Рассмотрим пример составления сетевого графика.