74. Вырожденный случай.

Рассмотрим задачу:

z=3x1 + 9x2 max

x1 + 4x2 8 ,

x1 + 2x2 4 ,

x1, x2 0.

Введя балансовые переменные x₃и x₄, решим обычный симплекс метод:

	Х1	Х2	Х3	Х4	Ci
X3	1	4	1	0	8
X4	1	2	0	1	4
L	-3	-9	0	0

	Х1	Х2	Х3	Х4	Ci
X2	1/4	1	1/4	0	2
X4	1/2	0	-1/2	1	0
L	-3/4	0	9/4	0	18

	Х1	Х2	Х3	Х4	Ci
X2		1	1/2	-1/2	2
X1	1	0	-1	2	0
L	0	0	3/2	3/2	18

На начальной итерации в качестве исключаемой переменной можно выбрать как x3 , так и x4. Выбрана переменная x3 , тогда переменная x4, оставаясь базисной на итерации 1, принимает нулевое значение, а это приводит к получению вырожденного базисного решения. Оптимальное решение задачи получается на следующей итерации. Сравнивая итерации 1 и 2, заметим следующее: хотя состав базисных и небазисных переменных на этих итерациях различен, значения всех переменных и целевой функции не изменяются:

x1 = 0, x2 = 2, x3 = 0, x4 = 0, L= 18.

Это обстоятельство может привести к выводу о целесообразности прекращения вычислений на итерации 1 (когда впервые обнаруживается вырожденность), хотя полученное решение не является оптимальным.

75. Нахождение исходного (опорного) базисного решения задачи лп.

Каноническая задача линейного программирования в векторной форме имеет вид:

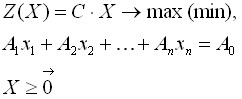
Положительным координатам допустимых решений ставятся в соответствие векторы условий. Эти системы векторов зависимы, так как число входящих в них векторов больше размерности векторов.

Базисным решением системы называется частное решение, в котором неосновные переменные имеют нулевые значения. Любая система уравнений имеет конечное число базисных решений, равное  , где   – число неизвестных,   – ранг системы векторов условий. Базисные решения, координаты которых удовлетворяют условию неотрицательности, являются опорными.

Опорным решением задачи линейного программирования называется такое допустимое решение  , для которого векторы условий, соответствующие положительным координатам  , линейно независимы.

Число отличных от нуля координат опорного решения не может превосходить ранга  системы векторов условий (т.е. числа линейно независимых уравнений системы ограничений).

Если число отличных от нуля координат опорного решения равно  , то такое решение называется невырожденным, в противном случае, если число отличных от нуля координат опорного решения меньше  , такое решение называется вырожденным.

Базисом опорного решения называется базис системы векторов условий задачи, в состав которой входят векторы, соответствующие отличным от нуля координатам опорного решения.

Теорема. Любое опорное решение является угловой точкой области допустимых решений.

Теорема. Любая угловая точка области допустимых решений является опорным решением.