Дослід№16. Аналітичне рішення алгебраїчних і диференціальних рівнянь

У цьому досліді ми розповімо, як аналітично вирішувати алгебраїчні і диференціальні рівняння.

• Спочатку знайдемо символьне рішення алгебраїчного рівняння.

• Уведіть рядок t=solve('x3-z*x=0','x'). Убудована функція solve (Обчислити) вирішує рівняння x^3-z*x=0 щодо змінної х.

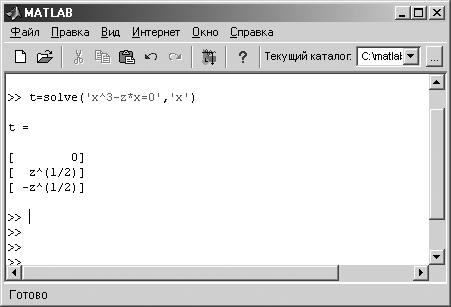
Рис. 24. Аналітичне рішення алгебраічного рівняння

• Натисніть клавішу Enter. У вікні програми з'явиться аналітичне рішення введеного рівняння (Рис. 24).

Для рішення системи алгебраїчних рівнянь варто вказати дані рівняння як аргументи функції solve (Обчислити).

MATLAB на відміну від програми Mathcad дозволяє дуже просто знаходити символьне рішення диференціальних рівнянь у формі Коші, тобто виду у'=f(y,x). Давайте розв’яжемо рівняння у'(x)=y(x)+sin(x).

• Наберіть на клавіатурі рядок t=dsolve('Dy=y+sin(x)', 'х'). Вбудована функція dsolve аналітично вирішує диференціальне рівняння Dy=y+sin(x), у якому символ D означає узяття похідної, щодо змінної х.

• Натисніть клавішу lEnterl. У вікні програми з'явиться аналітичне рішення введеного диференціального рівняння (Рис. 25).

Рис. 25. Аналітичне розв’язання диференційного рівняння

Зверніть увагу, що в символьному рішенні рівняння присутнє рядок С1, що означає довільну постійну. Варто помітити, що функція dsolve дозволяє вирішувати і системи диференціальних рівнянь, які потрібно вводити як аргументи даної функції.

Дослід№17. Використання вбудованої довідкової системи

У цьому досвіді ми розглянемо, як одержувати зведення по потрібному розділі програми MATLAB і опис необхідної функції за допомогою вбудованої довідкової системи.

Спочатку одержимо довідку по двомірній графіці.

• Натисніть кнопку ? на панелі інструментів. На екрані з'явиться вікно допомоги (Рис. 26).

• У центральній частині вікна допомоги розташований список розділів довідкової системи.

• У списку двічі клацніть мишею на розділі Двомірні графіки (Two dimensional graphs). У центральній частині вікна з'явиться короткий опис двомірної графіки.

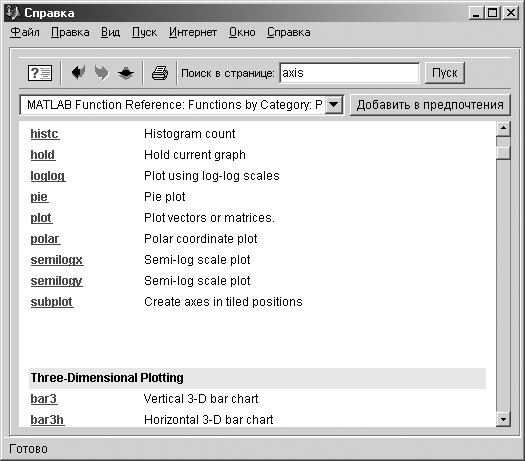
Рис. 26. Вікно допомоги

При необхідності можна і далі відображати нові розділи. Наприклад, щоб одержати довідку по функції plot (Графік), потрібно вибрати розділ plot (Графік).

Тепер знайдемо опис функції косинуса по її імені.

• Уведіть назву функції cos у поле введення, що розташовано в лівому верхньому куті вікна допомоги.

• Натисніть клавішу Enter. У центральній частині вікна з'явиться короткий опис функції косинуса.

Слід зазначити, що кнопка Назад (Back) дозволяє повернутися до попереднь переглянутого довідкового документу. Для одержання короткої довідки по функції необов'язково відкривати вікно допомоги, досить викликати команду HELP (Допомога) з параметром імені функції у вікні програми.

Дослід№18. Довідкова система з інтерфейсом Всесвітньої павутини

Довідкова системи Help Desk (Довідковий стіл) містить докладні зведення про програму, має інтерфейс Всесвітньої павутини, зручна в роботі. Для використання системи Help Desk (Довідковий стіл) необхідна програма Internet Explorer [Інтернет Эксплойер] чи інша програма для роботи з Всесвітньою павутиною. У цьому досвіді ми розповімо, як шукати опис функції по її імені в системі Help Desk (Довідковий стіл) і копіювати довідкові приклади у вікно програми MATLAB.

Щоб одержати опис функції обчислення залишку від розподілу mod, виконайте наступні кроки:

• Натисніть кнопку Довідковий стіл (Go to Help Desk) у вікні допомоги. Буде запущена програма Internet Explorer, у вікні якої відобразиться початкова сторінка системи Help Desk (Довідковий стіл) (Рис. 27).

• На початковій сторінці відображаються розділи довідкової системи Help Desk (Довідковий стіл). Для пошуку опису потрібної чи функції роздягнула можна переміщатися по розділах, клацаючи мишею по посиланнях, але швидше знайти довідку по імені функції.

• Введіть назву функції mod у поле введення Go to MATLAB function (Перейти до функції MATLAB).

• Натисніть кнопку Go (Перейти). У вікні програми Internet Explorer з'явиться опис функції mod і приклади її використання (Рис. 32).

• Скопіюємо приклад функції mod у вікно програми.

• У вікні програми Internet Explorer установите покажчик миші на початку рядка mod(13,5).

• Натисніть і утримуйте ліву кнопку миші.

• Не відпускаючи ліву кнопку миші, підведіть покажчик миші до кінця рядка mod(13,5). При переміщенні миші даний рядок буде виділятися темним кольором.

• Відпустите ліву кнопку миші. Рядок mod(13,5) буде виділена.

• Виберіть команду меню Виправлення " Копіювати (Edit Ф Сміттю). Виділений рядок буде скопійована в буфер обміну.

• Натисніть кнопку в правому верхньому куті вікна програми Internet Explorer, щоб завершити роботу даної програми.

• Натисніть кнопку Закрити (Close) у вікні допомоги. Вікно буде закрито.

• Натисніть кнопку на панелі інструментів вікна програми MATLAB. У вікні програми з'явиться рядок mod(13,5), уставлена з буфера обміну.

• Натисніть клавішу Enter. У вікні програми з'явиться результат обчислення залишку від розподілу 3.

На цьому наші досвіди з програмами Mathcad і MATLAB закінчені. Сподіваємося, що тепер ви зможете ефективно робити необхідні математичні розрахунки.

№\вар.		1	2	3	4	5	6	7	8	9	10
1	найпростіші обчислення	а)(a*b^a+10)/(a+2*b^a) б)(25+30*a)^(a-b)	а)(а^b*10b)/(14.5*a-b) б)√a*0.5*b+5/3*a-1/3*b	а)a/(b+4/7)-b/(7/3*a+a) б)(a^b+b^a)/(b/a+2*a/b)	а)16.5*1/3-5.6*a-2/3*b^1/2 б)(7e-a^(b-1/a))/3	а)b^2e-e^2/a б)4/7*a-5^6.5*b^e	a)3/(a*b^2)-e^(a*b^(a-1)) б)(3.6*5/3*b)/(a^2-b^3)	a)a*√b+√(a^(2*e/3))-a/b^(-2) б)0.5*b^a-(1/3)^(5*a)	a)a^e-b^e/(a*(b+2.3)-a^b) б)7^(-1.3)+a*b^(5+a^e)	a)2/3*e^(a-3b)+a^(-5/6) б)а*b^e-1/7*b/e	a)(5+1/3)/(e/a+b^(e*a)) б)-9*(a/(-4/3)+b^(a^(e-b/2))
2	операції з матрицями	a)[2,3,4.5;a,2*b,1.2;5,a/2,b^2] б)[a-b,4.1,a+b;a^2,4-b,4;5+b/2,4.1,a.5]	а)[3,4,5.2;a,5,b;a+b,6,2] б)[b,5;a,4.5;b-a,2.3]	a)[2*a,b/2,5;5-b,4,9;3,5,6.4] б)[3,b/4,3*a;1.1,0.5*a;5,3.2,1]	a)[a,b,a;a-b,b-a,a+b;a^2] б)[a,a;b,b;a/2,b/2]	a)[1,a;b,3] б)[a^2,b/3;b,b-5]	a)[3,4,5;a,b,a;4,3.1,2] б)[3,6,a/0.4;a/3,b,2.2*b;0.7*b,a,2*a]	a)[5,3,1;6,3,a;b,a,7] b)[b.1,5-a,6;0.5,a,a;b,0.3,b]	a)[1,2,3;3,2,1;a,4,a] б)[b,2*b,a;7,b,3.1;2.2,a*b,4]	a)[2,3,5;a,b,a;4,3,b/3.2] б)[0.5,a,b;b-3*a,b,a;1,1,2]	a)[6,5,7;a*b/4,a,b;4,a/2,b*2] б)[a-1,b+1,a+b;3,9,3;a+0.6,12,9]
3	побудова графіків	y=2*sin(x)	y=1/3*cos^2(x)	y=(a+2)/5*sin(x)	y=2^(b/6)*cos(x)	y=1/2*sin^2(x)	y=2/3*cos(x^2)	y=x^2+b*x^(-2)	y=a*sin(x^2)+x^(b*e)	y=2*e^2*sin^2(x)	y=3*e^a*sin(x^2)
4	тривимірні поверхні	z=a+sin(b+√(x^2+y^2))	z=sin(√y+√x+b)	z=cos(a*x^2-b*y^2)	z=cos(a/2*√x^3+b*y)	z=sin(a+x^2)+b*cos(y)	z=sin((x-b*y)^2)	z=cos^2(b+y^2-√x)	z=a*sin^2(x)+b*cos^2(y)	z=1/2*cos(√(b*x+a*y))	z=a*√(sin^2(x-y))
5	анімаційна графіка	y=a+sin(x)/√(x)	y=2*cos^2(x)+b	y=2^(b/6)*cos(x)	y=2/3*cos(x^2)	y=2*e^a*sin(x)	y=(a+2)/5*sin(x)	y=2*sin(x^a)	y=3*sin(x^2)	y=sin(x^2)/√x	y=x^2+cos^2(x)/2

Варіанти завдань до лабораторної роботи

“Вступ в MatLab”

6	рішення системи лінійних рівнянь	x^2+y^2=b x/2-y/2=a	x^3+a*y^2=a+b 3x+2y^2=4*b	sin(x)+2cos(y)=6-b cos^2(x)-2sin^2(y)=a	х+2у=a 4х+5у=b	2*√x+b*√y=18 4*x^2-8y^2+b=a	2*sin(x)+y^2=5-2*b a*x-b*cos(y)-3*a=-5*x	3x^2+a*y=12-b 4x-5*y^2=15+a	√x^2-√y^2=x*y a*x+b*y=x^2*Y2	(x-y)^2-a*b/2=25 3x^2+4y^2=12	x*y+a*y^2=6*a sin(x)/√y+y^2=14-3*b
7	пошук мінімуму функції	y=cos(x)/x	y=2*sin(x)/x	y=cos^2(x^2)/(2x)	y=sin(x)/√(x)	y=√x*sin(x^2)	y=x^2/2*tg(2x)	y=x/2sin(x)	y=x^3/cos(x/2)	y=2sin(2x)/cos(x)	y=tg(3x)/√x
8	пошук кореня нелінійного рівняння	3*x+cos(x)-5	x-cos(x*2)-1	2*x+sin(x)-2	x+sin(x)-10	2*x+sin(x)-2	0.5*x+cos(x)-5	0.2*x+sin(x)-8	x+cos(0.5*x)-2	x+cos(x)-1	x-cos(x)-3
9	чисельне інтегрування	x+cos(x)	cossin (x)-5*x	0.2*x+cos(x*3)	5*x-cos(x)	x-tan(x*2)	sin(x)-x*4	sin(x*3)+6	4-cos(2*x)	cos(x)-in(x)	sin(x)-2*x
10	створення нових функцій	tan(x)+cos(x)	2*sin(x)-cos(y)	cos(x)3	cos(x)-sin(x)	1/sin(x)	cos(x)+sin(x)+tan(x)	sin(x)3+ cos(x)3	tan(x)3	sin(x)*cos(x)	sin(x*x)-sin(x)
11	рішення диференціальних рівнянь	y’(x)-5*y(x) = sin(x2)	y’(x)=cos(x)2+sin(x)	y’(x) = cos(x)*y(x)	y’(x)- cos(x)* sin(x) = 0	y’(x)-2*y(x) 2 = y(x)3	y’(x) - y(x)/2 = sin(x)	y’(x) = 2*cos(x)2	y’(x) = sin(x)+cos(x)	y’(x)-y(x) = cos(x)2	y’(x)/5 = sin(x)3
12	аналітичне обчислення похідної та інтеграла	y’(x)=cos(x)/(2-sin(x))	y”(x) =5-cos(x3)	y’(x) = log(x2)	y”(x) = x5*cos(x)	y’(x) = 1/(cos(x)-sin(x))	y’(x) = log(x)+x	y”(x) = 5*x4/sin(x)	y’(x) = log(x)2	y”(x) = x-2-2*sin(x4)	y’(x) = (cos(x)2+cos(x4))/x4

13

символьні операції з мат. вираженнями й матрицями

а)

cos(x)2+sin(x)2

(1-cos(2*x))* cos(x))/sin(x)

tan(x)*cos(x)

1+(sin(x))2+ (cos(x))2

(1-sin(x))* (1+sin(x))

б)

2*x3-2*x2+2* sin(x)*x-2*sin(x)

x4+1/10*x3+x2+1/10*x

x(9/2)+5*x4+x(5/2)+5*x2

x10+x8+5*x5+5*x3

(cos(x)-3)*x4+ (-cos(x)+3)*x3

x3+2*x2-25*x-50

-9*(x^4)+72*(x^3)-54*(x^2)+432*x

1/2*x5-4*x3-6*x2+48

(1-cos(x))* (cos(x)2+5)

x^3+sin(x)*x^2-5*x-5*sin(x)

в)

(x2+6)*(8-x)* (9*x)

(x-5)*(2+x)* (x+5)

(cos(x)-3)* (x4-x3)

(x2+1)* (0.1*x+x2)

(x+9)*(6-x)* (x-5)

(sin(x)+x)* (x2-5)

(x-2)* (x+9)* (9-x)

(1-cos(x))* (cos(x)2+5)

(x2-8)*(0.5*x3-6)

(tan(x)2-x*2)* (x-4)

14

аналітичне вирішення алгебраїчних і диференціальних рівнянь

а)

5-z=x2/5

(x2-5)*z=0

x/z=6-x3

x3/5=z*x-5

x1/2-5*x=z

x3-z*x=0

x2=(z-2)*x

2*z*x-x1/2=2

0.5*z-x2=6

x3/5=z*x-8

б)

y’(x)-2*y(x) 2 = y(x)3

y’(x) = sin(x)+cos(x)

y’(x) = cos(x)*y(x)

y’(x)/5 = sin(x)3

y’(x) = 2*cos(x)2

y’(x)-y(x) = cos(x)2

y’(x)=cos(x)2+sin(x)

y’(x) + 2*y(x) =cos(x)/4

y’(x)- cos(x)* sin(x) = 0

y’(x) = y(x)3 + y(x)2

Коментарі

“a” i ”b”- дві останні цифри номеру залікової книжки.

1.Операції з матрицями:

Знайти квадратні корені, визначники, власні числа, добуток (звичайний та по елементний) матриць а та б.

2.Побудова графіків і діаграм:

Побудувати графіки, діаграми та гістограми відповідних функцій з довільним діапазоном значень.

3.Тривимірні поверхні:

Побудувати тривимірні поверхні та контурні графіки зі зміною забарвлення та освітлення (з довільним діапазоном змін).

4.Анімаційна графіка:

Побудувати двовимірні та тривимірні анімаційні графіки.

5.Пошук мінімуму функції:

Мінімізувати функцію у визначеному діапазоні.

6.Символьні операції з математичними вираженнями і матрицями:

а)спрощення виразу;

б)розкладання математичного виразу;

в)розкладання математичного виразу по степеням полінома.

7. Аналітичне рішення алгебраїчних і диференціальних рівнянь:

а)символьне рішення алгебраїчного рівняння;

б)символьне рішення диференціального рівняння у формі Коші.

8