11. Частотное управление асинхронными двигателями.

Использование АД в регулируемом электроприводе представляет особый интерес, т.к. АД является наиболее простым, дешевым и надежным двигателем. Возможности его регулирования, обеспечиваются изменением частоты, U и I статорной обмотки. Для реализации этой возможности питание двигателя необходимо осуществлять от управляемого преобразователя частоты. В качестве преобразователей частоты могут использоваться электромашинные и статические преобразователи. При частотном управлении АД возникает необходимость, регулировать не только частоту, но и величину подводимого U, причем U регулируется не только в функции частоты, но ещё и в функции нагрузки двигателя. Регулирование U в функции частоты и нагрузки можно осуществить лишь в замкнутых системах.

Законы частотного регулирования

При выборе соотношения между частотой и напряжением, подводимым к статору АД, чаще всего исходят из условия сохранения перегрузочной способности двигателя для любой из его регулировочных механических характеристик. Основной закон частотного регулирования (закон Костенко) в математической форме имеет вид

, где М_С и М^’_C -статические моменты сопротивления соответствующие скорости двигателя при частотах f₁ и f^’₁; U₁ и U^’₁ -соответствующие частотам f₁ и f^’₁ напряжения.

З-н изменения U определяется не только частотой источника питания, но и хар-ом изменения момента сопр-я механизма на валу двигателя при изменении угловой ск-ти.

Мех. хар-ки двигателя при этом законе изображены на рис. Жесткость хар-к сохраняется высокой. Критический момент в зоне частот, близких к основной, остается неизменной. Влияние падения U на r₁ становится весьма заметным, к намагничивающей цепи двигателя подводится тем меньшее U, чем меньше частота. Это вызывает ↓ критического момента, →, перегрузочной способности двигателя.Плавное регул-е до f₁=0 при этом законе невозможно. Невозможно также обеспечить устойчивую работу двигателя при М_с=const в широком диапазоне регулирования частоты.

Закон пропорционального регулир-я можно легко реализовать при разомкнутой системе. Этот закон целесообразен только для крупных АД, потери в двигателе больше, чем при основном законе. М ех. хар-ки при этом законе изображены на рис.

Механические характеристики при этом законе изображены на рис. При постоянной мощности статической нагрузки Р_С=const или : В этом случае Х=-1 Приняв ₀=0, получим закон управления

или

Статические механические характеристики ад при частотном управлении.

Для получения основных соотношений воспользуемся Т образной схемой замещения АД, которая наиболее точно отражает реальные физические процессы в двигателе.

Здесь

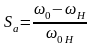; ; , S_а – абсолютноескольжение.

При пропорциональном законе управления , который графически можно представить в виде прямой (см. график). Точке А, для которой f₁=f_1H (₁=1) и U₁=U_1H (V₁=1) , соответствует естеств. хар-ка двигателя, которая изображена на следующем рис. Здесь приведено семейство мех. хар-к при ₁<1. Перегрузочная способность двигателя ↓, особенно при ₁ <0,5. ↓ М_кр ограничивает диапазон регулирования, т.к. при некоторой частоте перегрузочная способность будет очень малой.

При ↓ частоты начинает сказываться влияние падения U на акт. сопр-ии r₁, которое от частоты не зависит. Все большая часть пит. U начинает прикладываться к r₁ , а к остальной части схемы, в том числе к цепи намагничивания, - меньшая. Т.о. закон пропорционального управления не очень хорош.

В ыход из положения - при уменьшении f₁ напряжение U₁ уменьшать в меньшей степени (смотри пунктир на графике V₁=f(₁)).

М ех. хар-ки в этом случае будут иметь вид, изображенный на следующем графике. Можно подобрать такую зависимость V₁ от _, которая обеспечит постоянство критич. момента при изменении частоты, в том числе и при ₁=0. При малых частотах ток, потребляемый двигателем, больше, чем на естеств. хар-ке и двигатель сильно греется. Если же ему обеспечить номинальный нагрев, то придется уменьшить U, что приведет к ↓Мкр. Получается, что принципиально невозможно обеспечить закон V₁=f(₁), при котором удовлетворялись бы 2 противоречия, т.е. обеспечение перегрузочной способности и нормального нагрева двигателя при снижении частоты. Данный закон регулирования может быть обеспечен лишь при условии, если U изменяется не только в функции частоты, но и нагрузки на валу двигателя.

Управление при _s=const. Этот случай соответствует такому регулированию напряжения, приложенного к статору, при котором обеспечивается компенсация падения напряжения на r₁. ЭДС e_s=e₁ в этом случае становится независимой от нагрузки, т.е. становится постоянной при данном значении частоты. При изменении частоты нужно изменять напряжение. Пропорционально изменению частоты будет изменятся и e_s . Это соответствует стабилизации потокосцепления . Если же будет изменяться нагрузка, то дополнительно нужно регулировать напряжение т.о., чтобы скомпенсировать изменившееся падение напряжения на r₁ и этим самым обеспечить как постоянство e_s, так и постоянство потокосцепления _S.

Уравнение механической характеристики примет вид.

;

П ри изменении частоты нужно пропорционально изменять и Еm, что и соответствует компенсации падений напряжения на r₁ и x₁ . Уравнение механической характеристики:

;

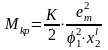
Анализ показывает, что в этом случае получим увеличение Мкр примерно в 2 раза при всех частотах по сравнению с Мкр на естественной характеристике. При снижении частоты относительная жесткость характеристик возрастет.

Если напряжение, подводимое к статору, регулировать т.о., чтобы компенсировать падение напряжения и на r₁ и на x₁ и на x^l₂, то можно обеспечить _r=const. В этом случае можно считать, что двигатель питается напряжением E_r , а не U₁ и .

Компенсация падений напряжения на r₁, x₁, x₂^’ равносильна тому, что как - будто этих сопротивлений нет вообще, следовательно b=0;с=0;d=0;е=1. Уравнения механических характеристик и Мкр принимают вид (вместо V₁ подставляем e_r):

;

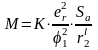Зависимость М от скольжения линейна. Характеристики получаются такими, как у компенсированной машины постоянного тока независимого возбуждения. Перегрузочная способность теоретически равна . Именно этот вариант и реализуется в современных системах частотно регулируемых электроприводов.

В принципе и это не является пределом. При компенсации падения напряжения ещё и на r₂^’ можно получить абсолютно жесткую механическую характеристику с постоянным скольжением (см. график).

Т.о. только при реализации рассмотренных здесь законов возможности АД используется полностью.