3. Системы управления и регулирования. Использование структурных схем. Законы управления. Принципы управления, качество.

Автоматическая система - совокупность управляемого объекта и автоматического управляющего устройства, взаимодействующих между собой. Автоматическая система регулирования - автоматическая система с замкнутой цепью воздействий, в которой управляющие воздействия вырабатываются в результате сравнения действительных значений управляемой величины с предписанными значениями.

Использование структурных схем

Для оценки точности, устойчивости и качества управления замкнутых систем необходимо знать их уравнения статики и динамики. Уравнение динамики замкнутой системы можно получить на основе совокупности уравнений отдельных элементов, образующих систему, путем последовательного исключения промежуточных переменных. Наиболее удобным для решения этой задачи объединения математических моделей элементов является метод структурных преобразований, согласно которому по структуре схемы с помощью нескольких простых правил находят ее общую (эквивалентную) передаточную функцию, а затем – соответствующее уравнение динамики. Структурные схемы САУ  это графическое изображение САУ, где динамика процессов представлена в операторной форме в виде передаточных функций. Структурная схема отличается от функциональной тем, что элементы представляются математическими моделями, т.е. зависимостями выход-вход. Для упрощения (свертывания) сложных алгоритмических схем применяют правила преобразования, с помощью которых определяют эквивалентные передаточные функции типовых соединений звеньев.

Законы управления

Типовые законы регулирования линейных систем:

1. П (пропорциональный) – регулятор :

Преимуществами данного регулятора являются простота и быстродействие, а недостатком – ограниченная точность.

2. И ( интегральный ) – регулятор :

Преимуществом данного регулятора является лучшая по сравнению с П-регулятором точность установки режима, а недостатками – худшие по сравнению с П-регулятором показатели качества, а именно большая колебательность и меньшее быстродействие.

3. ПИ – регулятор :

О бъединяет два регулятора П и И, следовательно обладает наилучшими свойствами по сравнению с вышеописанными регуляторами, а именно за счет П-составляющей улучшается показательные качества в переходном процессе, а за счет И-составляющей уменьшается ошибка регулирования  т.е. улучшается точность.

4. Д ( дифференциальный ) – регулятор :

Преимуществом данного регулятора является то, что Х(р) зависит от дифференциальной ошибки и регулятор реагирует на малейшее изменение ошибки, однако очень большим недостатком является плохая помехоустойчивость(очень чувствительный). На практике практически не используется в чистом виде, как и идеальное дифференцирующее звено.

5. ПД – регулятор:

О бъединяет два регулятора П и Д, за счет П-составляющей уменьшается чувствительность регулятора, а за счет Д-составляющей – лучшее быстродействие, недостатком является ограниченная точность.

6. ПДИ – регулятор:

О бъединяет три регулятора П, И и Д, обладает преимуществами всех регуляторов, а недостатком является сложность реализации.

Принципы управления

Общая структура проектируемой системы, ее основные элементы и принципы управления в значительной степени определяются свойствами объекта управления, условиями работы системы и требованиями предъявляемыми к ее точности. САУ должна решать 2 основные задачи: 1) Обеспечение требуемого изменения регулируемой величины; 2) Скомпенсировать действие на объект регулирования возмещения.

1) Принцип замкнутого управления.

Y (p) = Wр(p)*Wo(P)*X(p). Алгоритм управления строится только на основе заданного алгоритма функционирования и не контролируется по фактическому значению управляемой координаты.

2) Принцип обратной связи (принцип управления по отклонению контролируемой функции от входного воздействия, принцип Ползунова-Уатта).

Регулятор вступает в работу только тогда, когда между текущим и заданным значениями регулируемой функции появляется рассогласование, и регулятор воздействует на объект таким образом, чтобы свести это рассогласование к нулю или к малой величине.

3) Принцип управления по возмущению (принцип компенсации, принцип Понселе).

Y (p)= Wp(p)Wor(p)R(p)+[Wkf(p)Wp(p)Wor(p)-Wof(p)]F(p); Возмущение измеряется и формируется управляющее воздействие по каналу возмущения на объект так, чтобы скомпенсировать влияние возмущения на регулируемую координату.

4) Комбинированный принцип управления

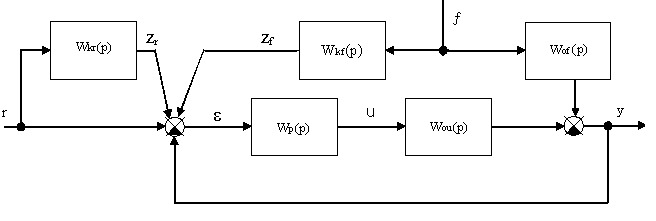
Так как регулирование производится по отклонению, то возможно регулирование объектов с любыми динамическими свойствами, а наличие дополнительных связей по возмущению и входному воздействию позволяет добиться высокой точности регулирования без существенного усложнения замкнутого контура регулирования.

Критерии и показатели качества.

1)Точность в установившемся режиме работы САУ. Показатели: статическая ошибка, статизм системы.

2)Вид переходного процесса. Показатели: время регулирования, перерегулированияи др.

3)Устойчивость. Показатели: запас устойчивости по модулю, по фазе.

4)Чувствительность к изменению параметров передаточной функции объекта (датчика, обратной связи). Показатели: чувствительность системы

S(p)=[dWз(p)/dWo(p)]*[Wo(p)/Wз(p)]

5)Способность компенсировать возмущения. Показатели: статическая и динамическая ошибка по каналу возмущения.