Основы теории управления [8-10] ФАЙЗРАХМАНОВ Р.А.

1. Устойчивость систем управления.

2. Математические модели объектов управления в системах управления. Формы представления моделей объектов в системах управления.

3. Системы управления и регулирования. Использование структурных схем. Законы управления. Принципы управления, качество.

4. Системы управления при случайных воздействиях. Преобразование стационарного случайного сигнала стационарной линейной динамической системой.

5. Основные задачи анализа систем с минимальной средней квадратичной ошибкой: задача фильтрации, задача экстраполяции, задача дифференцирования и др.

1. Устойчивость систем управления.

Объект управления - устройство (совокупность устройств), осуществляющее технический процесс, который нуждается в оказании специально организованных воздействий извне для выполнения его алгоритма функционирования. Управление - процесс осуществления воздействий, соответствующих алгоритму управления. Алгоритм функционирования - совокупность предписаний, ведущих к правильному выполнению технического процесса в каком-либо устройстве или совокупности устройств (системе). Алгоритм управления - совокупность предписаний, определяющая характер воздействий извне на управляемый объект с целью выполнения им заданного алгоритма функционирования. Устойчивость - свойство системы приходить в исходное состояние после снятия возмущения.

Кривые 1 и 2 характеризуют устойчивую систему, кривые 3 и 4 характеризуют системы неустойчивые. Системы 5 и 6 на границе устойчивости 5 - нейтральная система, 6 - колебательная граница устойчивости.

Пусть дифференциальное уравнение САУ в операторной форме имеет вид

Тогда решение дифференциального уравнения (движение системы) состоит из двух частей Вынужденное движение того же вида что и входное воздействие.

При отсутствии кратных корней где С_i-постоянные интегрирования, определяемые из начальных условий,

₁, ₂…, _n – корни характеристического уравнения

Корни характеристического уравнения не зависят ни от вида возмущения, ни от начальных условий, а определяются только коэффициентами а₀, а₁, а₂,…,а_n, то есть параметрами и структурой системы.

1-корень действительный, больше нуля;2-корень действительный, меньше нуля;3-корень равен нулю;4-два нулевых корня;5-два комплексных с опряженных корня, действительная часть которых положительна; 6-два комплексных сопряженных корня, действительная часть которых отрицательная;7-два мнимых сопряженных корня.

Теоремы А.М.Ляпунова:

Теорема 1. Если определяющее (характеристическое) уравнение имеет корни только с отрицательными вещественными частями, то невозмущенное движение устойчиво и притом асимптотически, независимо от членов выше первого порядка малости.

Теорема 2. Когда среди корней определяющего (характеристического) уравнения находятся такие, вещественные части которых положительные, невозмущенное движение неустойчиво.

Критерий устойчивости - это правило, позволяющее выяснить устойчивость системы без вычисления корней характеристического уравнения.

Раус установил: Необходимое (но не достаточное) условие устойчивости САУ есть положительность коэффициентов характеристического уравнения системы.

Критерий устойчивости Гурвица: Для устойчивости системы необходимо и достаточно, чтобы при положительном коэффициенте характеристического уравнения a₀ главный определитель Гурвица и все его диагональные миноры были положительны. Пусть определено характеристическое уравнение замкнутой системы: уравнение приводим к виду, чтобы a₀>0.Главный определитель Гурвица имеет вид:

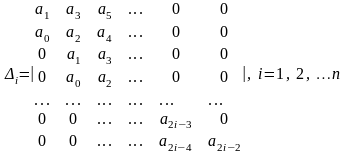
Критерий Найквиста:

1.Система в разомкнутом состоянии устойчива. Критерий: Если разомкнутая цепь системы устойчива, то для устойчивости замкнутой системы необходимо и достаточно, чтобы АФЧХ разомкнутой цепи не охватывала т.(-1;j0).

Н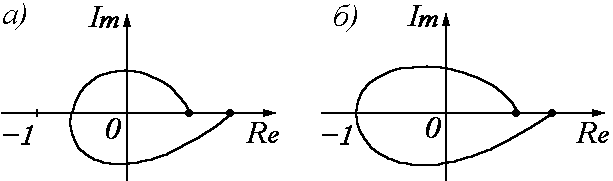 а рисунке а) изображен годограф системы, устойчивой в замкнутом состоянии, а на б) – системы, находящейся на границе устойчивости.

2.Система имеет в разомкнутом состоянии полюсы на мнимой оси. Критерий: Если передаточная функция разомкнутой цепи системы имеет кроме полюсов с отрицательной вещественной частью так же 0 или чисто мнимые, то для устойчивости замкнутой системы необхо и достаточ, чтобы АФХ разомкнутой системы с ее дополнением в ∞, не охватывала т.(-1;j0).

Д ля анализа устойчивости системы АФХ дополняют окружностью бесконечно большого радиуса при 0 против часовой стрелки до положительной вещественной полуоси при нулевых полюсах, а в случае чисто мнимых корней - полуокружностью по часовой стрелке в точке разрыва непрерывности АФХ.

3. Разомкнутая система устойчива, замкнутая система неустойчива. Критерий: Для устойчивости замкнутой системы, разомкнутая цепь которой неустойчива, требуется, чтобы амплитудно-фазовая характеристика разомкнутой цепи (с дополнением в бесконечности для систем с нулевыми и чисто мнимыми полюсами передаточной функции разомкнутой системы) охватывала точку (-1, j0) против часовой стрелки на угол m, где m - число полюсов с положительной вещественной частью в передаточной функции неустойчивой разомкнутой цепи системы.

Критерий Цыпкина: Замкнутая система устойчива, если при изменении  от нуля в сторону положительных значений до  разность числа положительных и отрицательных переходов АФХ разомкнутой системы через полупрямую (-, -1) равна m/2.

Критерий Найквиста для ЛЧХ: Для того чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при всех значениях , где L()>0, разность числа положительных и отрицательных переходов фазовой характеристики разомкнутой системы через линии (2k+1) (k=0,1,2,…) равнялась m/2, где m - число полюсов с положительной вещественной частью в передаточной функции разомкнутой цепи системы.