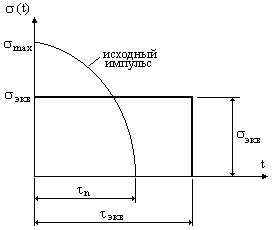
Метод эквивалентных прямоугольных импульсов.

Если неравенство 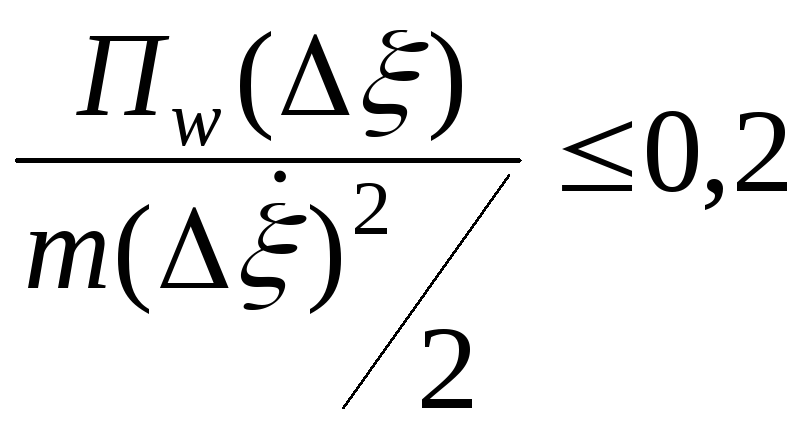не выдерживается, то необхо­димо применить более точный метод расчета. В методе эквивалентных прямоугольных импульсов возможен учёт как кинетической, так и потенциальной энергий объекта в любой момент времени.

Удар по основанию.

; W=0 - т.к. блок при мгновенном воздействии не успевает сдвинуться с места. - реальное движение объекта. Блок успел сдвинуться на некоторую величину - -.

За время действия импульса блок успел сместиться на некоторую ве­личину:

Т.о. в реальной ситуации деформация определяется и кинетической и потенциальной энергиями совместно.

Эквивалентный прямоугольный импульс.

Эквивалентный прямоугольный импульс - это такой импульс, при воздей­ствие которого на систему приращение смещения основания скорости объекта в конце удара равны смещению и скорости в конце действия исходного импульса. условие эквивалентности импульсов.

- приращение скорости основания за время действия эквивалентного прямоугольного импульса.

- перемещение основания при воздействии эквивалентного прямоугольного импульса.

Решая систему относительно иполучают параметры эквивалентного прямоугольного импульса.

Для типовых форм ударных импульсов иприводятся в таб­лицах.

Методика расчета.

Исходным является уравнение полной энергии системы А = Т + П. Распишем его через параметры эквивалентного прямоугольного импульса:

где W - смещение в любой момент времени;

- скорость в любой момент времени;

П_w(W) - потенциальная энергия амортизаторов при деформации W;

Для дальнейшего расчёта отроятся вспомогательные графики (- скорость от деформации) иW(t) (-смещение от времени). При этом удаётся проследить поведение системы в любой момент времени.

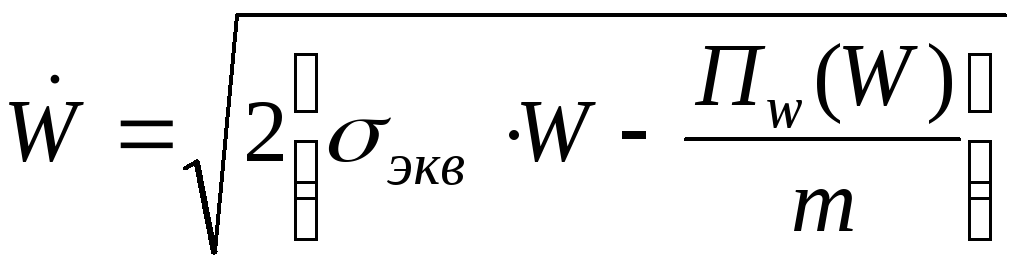- Расчет по формуле по точкам отстоящих друг от друга на расстоянии

Графики строятся в следующем виде (сначала , затемW(t)):

Построение графика: - время прохождения какого-либо участка

равно , деформация амортизатора равна размеру участ­ка делённого на среднюю скорость на участке, которая равна:

Например:

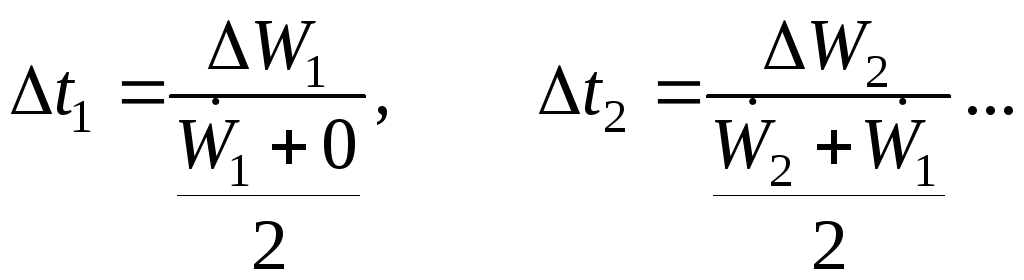
По границам иW(t) определяют значение скорости и деформации в момент .

Условие эквивалентности гарантирует точное определение параметров системы только при: . При этом определяют деформацию амортизаторов и скорость объекта. Приполученные значения скорости и деформации в системе соответствуют действительным. Во все остальные моменты времени параметры движения системы могут быть определены толь­ко приблизительно по данным графикам.

Кривая 2 - точная зависимость, рассчитанная аналитически. В точке при обе кривые (1 и 2) должны совпадать.

Далее вычисляем полную энергию системы. Предположим, что накопленные за время удара кинетическая и потенциальная энергии переходят в потенциальную энергию сжатых амортизаторов, тогда можно записать:

I - расчёт о данным; II - определяется по графику ударной энергоёмкости.

Далее определяем ускорение объекта по ранее указанной методике. Рассмотренные методики могут применяться при - упрощённая методика и - методика эквивалентного прямоугольного импульса, где Т - период собственных колебании системы, полученный из вибрационного расчёта.