10. Индексация. Достоинства и недостатки. Примеры
Самая распространённая задача, которую решают приложения работающие с базами данных - это поиск необходимых записей по заданному критерию.
Внутренняя модель данных рассматривает задачу хранения информации на внешних носителях с целью:
уменьшения внешней памяти.
уменьшения времени доступа к требуемой информации.
Эти цели достигаются при помощи использования факторизации и индексации.
Индексация используется для увеличения скорости доступа к данным за счет применения индекса.
Индекс - это таблица из 2-х полей, в которой первое поле является ключом индексации в сортированном порядке, а второе поле содержит указатель записи файла, в которой хранится ключ индексации.
Ключом индексации называется поле или часть поля или совокупность полей, по которым осуществляется поиск информации.
Указатель же (ссылка) используется для адресации объектов в памяти и может быть:- абсолютным адресом
- относительным адресом (состоящим из базы и смещения)
- каким-либо специальным символом или флажком, помечающим место хранения объекта.
Индекс позволяет производить дихотомический или двоичный поиск.
Индекс позволяет ускорить поиск и представить файл в отсортированном виде без физического перемещения записей.
Индекс можно хранить в памяти, так как он занимает мало места.
Виды индексов:
Плотный индекс позволяет точно определить, где найти каждый член.
Неплотный индекс дает возможность установить блок, который содержит данный член, но не позволяет точно определить в каком месте он находится.
В Уникальном индексе только один указатель может быть связан с соответствующим ему ключом. Уникальные индексы - это индексы строящиеся по первичному ключу.
Селективный индекс строится по некоторому подмножеству значений, выбираемому из множества возможных значений по определенном условию.
Основная идея Иерархического индекса заключается в том, что можно добиться повышения эффективности, используя индекс, позволяющий перейти к более детальному индексу, который в свою очередь, позволяется перейти к еще более детальному индексу и т.д. до тех пор, пока не будут достигнуты реальные данные.
Как бы не были организованы индексы в конкретной СУБД, их основное назначение состоит в обеспечении эффективного прямого доступа к кортежу отношения по ключу. Индекс определяется для одного отношения, и ключом является значение атрибута (возможно, составного). Если ключом индекса является возможный ключ отношения, то индекс должен обладать свойством уникальности, т.е. не содержать дубликатов ключа. На практике ситуация выглядит обычно так: при объявлении первичного ключа отношения автоматически заводится уникальный индекс, а единственным способом объявления возможного ключа, отличного от первичного, является явное создание уникального индекса. Это связано с тем, что для проверки сохранения свойства уникальности возможного ключа, так или иначе, требуется индексная поддержка.
Поскольку при выполнении многих операций языкового уровня требуется сортировка отношений в соответствии со значениями некоторых атрибутов, полезным свойством индекса является обеспечение последовательного просмотра кортежей отношения в диапазоне значений индекса в порядке возрастания или убывания значений.
Наконец, одним из способов оптимизации выполнения эквисоединения отношений (наиболее распространенная из числа дорогостоящих операций) является организация так называемых мультииндексов для нескольких отношений, обладающих общими атрибутами. Любой из этих атрибутов (или их набор) может выступать в качестве ключа мультииндекса. Значению ключа сопоставляется набор кортежей всех связанных мультииндексом отношений, значения выделенных атрибутов которых совпадают со значением ключа.
Общей идеей любой организации индекса, поддерживающего прямой доступ по ключу и последовательный просмотр в порядке возрастания или убывания значений ключа является хранение упорядоченного списка значений ключа с привязкой к каждому значению ключа списка идентификаторов кортежей. Одна организация индекса отличается от другой главным образом в способе поиска ключа с заданным значением.
Производительность
Для оптимальной производительности запросов индексы обычно создаются на тех столбцах таблицы, которые часто используются в запросах. Для одной таблицы может быть создано несколько индексов. Однако увеличение числа индексов замедляет операции добавления, обновления, удаления строк таблицы, поскольку при этом приходится обновлять сами индексы. Кроме того индексы занимают дополнительный объем памяти, поэтому перед созданием индекса следует убедиться, что планируемый выигрыш в производительности запросов превысит дополнительную затрату ресурсов компьютера на сопровождение индекса.
B-деревья
Видимо, наиболее популярным подходом к организации индексов в базах данных является использование техники B-деревьев. С точки зрения внешнего логического представления B-дерево - это сбалансированное сильно ветвистое дерево во внешней памяти. Сбалансированность означает, что длина пути от корня дерева к любому его листу одна и та же. Ветвистость дерева - это свойство каждого узла дерева ссылаться но большое число узлов-потомков. С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, т.е. каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.
Поиск в B-дереве - это прохождение от корня к листу в соответствии с заданным значением ключа. Заметим, что поскольку деревья сильно ветвистые и сбалансированные, то для выполнения поиска по любому значению ключа потребуется одно и то же (и обычно небольшое) число обменов с внешней памятью. Более точно, в сбалансированном дереве, где длины всех путей от корня к листу одни и те же, если во внутренней странице помещается n ключей, то при хранении m записей требуется дерево глубиной logn(m), где logn вычисляет логарифм по основанию n. Если n достаточно велико (обычный случай), то глубина дерева невелика, и производится быстрый поиск. Основной "изюминкой" B-деревьев является автоматическое поддержание свойства сбалансированности.
Хэширование
Альтернативным деревьям и все более популярным подходом к организации индексов является использование техники хэширования. Это очень обширная тема, которая заслуживает отдельного рассмотрения. Мы ограничимся лишь несколькими замечаниями. Общей идеей методов хэширования является применение к значению ключа некоторой функции гомоморфного отображения в адрес - свертки (хэш-функции), вырабатывающей значение меньшего размера. Свертка значения ключа затем используется для доступа к записи.
В самом простом, классическом случае, свертка ключа используется как адрес в таблице, содержащей ключи и записи. Основным требованием к хэш-функции является равномерное распределение значение свертки. При возникновении коллизий (одна и та же свертка для нескольких значений ключа) образуются цепочки переполнения. Главным ограничением этого метода является фиксированный размер таблицы. Если таблица заполнена слишком сильно или переполнена, но возникнет слишком много цепочек переполнения, и главное преимущество хэширования - доступ к записи почти всегда за одно обращение к таблице - будет утрачено. Расширение таблицы требует ее полной переделки на основе новой хэш-функции (со значением свертки большего размера).
В случае баз данных такие действия являются абсолютно неприемлемыми. Поэтому обычно вводят промежуточные таблицы-справочники, содержащие значения ключей и адреса записей, а сами записи хранятся отдельно. Тогда при переполнении справочника требуется только его переделка, что вызывает меньше накладных расходов.
В целом методы B-деревьев и хэширования все более сближаются.
Пример.
Файл а1:
-
адреса
А1
А2
А3
A0
d
1
F
A1
a
2
M
A2
C
3
F
A3
B
4
M
A4
Z
3
M
A5
I
2
F
A6
J
2
M
A7
k
5
M
Организуем индексацию по полю А1, индекс будет плотный, т.е. индексируются все значения ключа.
Запишем файл упорядоченный по полю А1:
-
B
A1
адрес
B1
A
A1
B2
B
A3
B3
C
A2
B4
D
A0
B5
I
A5
B6
J
A6
B7
K
A7
B8
Z
A4
Создадим индекс второго уровня, для этого разбиваем индекс на группы по три записи:
-
A1
адрес
C
B1
J
B4
z
B7
В первом столбце записан старший ключ, во втором столбце младший ключ.
Рассмотрим, например поиск записи с ключом I.
Смотрим в последнюю таблицу и ищем где ключ больший I, это J, его адрес B4, теперь обращаемся ко второй таблице, находим тройку записей, у которой младший индекс B4, это тройка D,I,J, находим в ней I, смотрим какой она имеет адрес – A5, обращаемся в первую таблицу и находим запись с адресом А5.
Индекс с инвертированными списками. Инвертированный список хранит список ключей для каждого значения где это значение встречается.
-
А3
Список адресов
F
A0, A2,A5
M
A1,A3,A4,A6,A7
11. В-дерево. Добавление и удаление элементов
Видимо, наиболее популярным подходом к организации индексов в базах данных является использование техники B-деревьев. С точки зрения внешнего логического представления B-дерево - это сбалансированное сильно ветвистое дерево во внешней памяти. Сбалансированность означает, что длина пути от корня дерева к любому его листу одна и та же. Ветвистость дерева - это свойство каждого узла дерева ссылаться но большое число узлов-потомков. С точки зрения физической организации B-дерево представляется как мультисписочная структура страниц внешней памяти, т.е. каждому узлу дерева соответствует блок внешней памяти (страница). Внутренние и листовые страницы обычно имеют разную структуру.
Поиск в B-дереве - это прохождение от корня к листу в соответствии с заданным значением ключа. Заметим, что поскольку деревья сильно ветвистые и сбалансированные, то для выполнения поиска по любому значению ключа потребуется одно и то же (и обычно небольшое) число обменов с внешней памятью. Более точно, в сбалансированном дереве, где длины всех путей от корня к листу одни и те же, если во внутренней странице помещается n ключей, то при хранении m записей требуется дерево глубиной logn(m), где logn вычисляет логарифм по основанию n. Если n достаточно велико (обычный случай), то глубина дерева невелика, и производится быстрый поиск.
Основной "изюминкой" B-дереве является автоматическое поддержание свойства сбалансированности.
Бинарные деревья представляют эффективный способ поиска. Бинарное дерево представляет собой структурированную коллекцию узлов. Деревья являются структурами несколько более сложными,чем списки.
Списки представляются обычно, как нечто линейное, в то время как деревья в естественном представлении имеют более одного измерения. Деревья обычно изображают растущими сверху вниз, с корнем наверху. Отдельные ячейки, из которых составляется дерево, называют узлами ( или потомками ). Узел, имеющий дочерние узлы, называется их родительским узлом. Аналогия с генеалогическим деревом позволяет ввести термины прародитель, предок и потомок. Узел, не имеющий дочерних узлов, называется листом. Хотя узел может иметь более одного дочернего, родительский узел может быть у него только один. Структура данных, в которой узлы имеют более одного родителя, не может считаться деревом. Единственым узлом, не имеющим родителя является корневой узел. В двоичном дереве у узла может быть один, два или ни одного потомка. Дочерний узел, расположенный левее родительского, называется левым потомком ( левым дочерним ). Дочерний узел правее родителя называют правым потомком.
Существенное
свойство двоичного дерева - это то, что
для каждого данного узла все узлы левее
его ( т.е. левый дочерний и все его потомки
) содержат значения, меньше значения
самого узла. Аналогичным образом все
узлы правее данного содержат большие
либо равные значения.
Левое поддерево поизвольной вершины X содержит ключи, не превосходящие key[X] ( значение вершины X ), правое - не меньшие key[X]. Разные бинарные деревья поиска могут представлять одно и то же множество. Время выполнения ( в худшем случае ) большинства операций пропорционально высоте дерева.
При представлении с использованием указателей для каждой вершины дерева нужно хранить помимо значения ключа key и дополнительных данных, также и указатели left, right, parent (на левое и правое поддерево, а также родителя). Если ребёнка ( или родителя - для корня ) нет, соответствующая переменная должна равняться NULL. Ключи в двоичном дереве поиска хранятся с соблюдением свойства упорядоченности: Пусть X - произвольная вершина двоичного дерева поиска. Если вершина Y находится в левом поддереве вершины X, то key[X]>=key[Y]. Если вершина Y находится в правом поддереве вершины X, то key[X]<=key[Y]
Типовые функции при работе с бинарным деревом.
Функция печати выводит на экран все ключи, входящие в дерево. x - вершина бинарного дерева, left[x] - левое поддерево, right[x] - правое поддерево, key[x] - ключ, p[x] - родитель вершины.
Печать(x)
Начало
1 если x не равен NULL
2 тогда Печать(left[x])
3 напечатать key[x]
4 Печать(right[x])
Конец
Процедура поиска. Получает на вход искомый ключ k и указатель x на корень поддерева, в котором производится поиск. Она возвращает указатель на вершину с ключом k ( если такая есть ) или NULL ( если такой вершины нет )
Поиск(x,k)
Начало
1 Пока x не равен NULL и k не равно key[x]
2 Начало
3 если k меньше key[x]
4 тогда x равно left[x]
5 иначе x равно right[x]
6 Конец
7 Вернуть x
Конец
Минимум и максимум. Минимальный ключ в дереве поиска можно найти, пройдя по указателям left от корня ( пока не дойдем до NULL ). Процедура возвращает указатель на минимальный элемент поддерева с корнем х.
Минимум(x)
Начало
1 Пока left[x] не равен NULL
2 Начало
3 x=left[x]
4 Конец
5 Вернуть x
Конец
Максимум(x)
Начало
1 Пока right[x] не равен NULL
2 Начало
3 x=right[x]
4 Конец
5 Вернуть x
Конец
Данный принцип демонстрируется на рисунке.
При поиске ключа 13 мы идём от корня по пути 15->6->7->13. Чтобы найти минимальный ключ 2, мы всё время идём налево. Чтобы найти максимальный ключ 20 направо.
Следующий и предыдущий элементы. Процедура возвращает указатель на следующий за x элемент или NULL в случае, если элемент x - последний в дереве.
ПолучитьСледующийЭлемент(x)
Начало
1 если right[x] не равен NULL
2 тогда вернуть Минимум(right[x])
3 y равно p[x]
4 пока y не равно NULL и x равно right[x]
5 Начало
6 x равно y
7 y равно p[y]
8 Вернуть y
Конец
ПолучитьПредыдущийЭлемент(x)
Начало
1 если left[x] не равен NULL
2 тогда вернуть Максимум(left[x])
3 y равно p[x]
4 пока y не равно NULL и x равно left[x]
5 Начало
6 x равно y
7 y равно p[y]
8 Вернуть y
Конец
Добавление.
Процедура добавляет заданный элемент в подходящее место дерево (такое место единственное), сохраняя свойство упорядоченности. Параметром процедуры является указатель z на новую вершину, в которую помещены значения key[z] ( добавляемое значение ключа), left[z]=NULL и right[z]=NULL. В ходе работы процедура меняет дерево T и возможно некоторые поля вершины z, после чего новая вершина c данным значением ключа оказывается вставленной в подходящее место (см. рисунок).
Вставка(T,z)
Начало
1 y равно NULL
2 x равно root[T]
3 пока x не равно NULL
4 Начало
5 y равно x
6 если key[z] меньше key[x]
7
тогда x равно left[x]
8 иначе x равно right[x]
9 Конец
10 p[z] равно y
11 если y равно NULL
12 тогда root[T] равно z
13 иначе если key[z] меньше key[y]
14 тогда left[y] равно z
15 иначе right[y] равно z
16
Конец
Удаление. Параметром процедуры удаления явяляется указатель на удаляемую вершину. При удалении возможны случаи, указанные на рисунке ниже. Если у z нет детей, для удаления z достаточно поместить NULL в соответствующее поле его родителя ( вместо z ). Если у z есть один ребёнок, можно вырезать z, соединив его родителя напрямую с ребенком. Если же детей двое, требуются некоторые приготовления: мы находим следующий ( в смысле порядка на ключах) за z элемент y; у него нет левого ребёнка. Теперь можно скопировать ключ и дополнительные данные из вершины y в вершину z, а саму вершину y удалить описанным образом.
Удаление(T,z)
Начало
1 если left[z] равно NULL или right[z]=NULL
2 тогда y равно z
3 иначе y равно ПолучитьСледующийЭлемент(z)
4 если left[y] не равно NULL
5 тогда x равно left[y]
6 иначе x равно right[y]
7 если x не равно NULL
8 тогда p[x] равно p[y]
9
10 если p[y] равно NULL
11 тогда root[T] равно x
12 иначе если y равно left[p[y]]
13 тогда left[p[y]] равно x
14 иначе right[p[y]] равно x
15 если y не равен z
16 тогда key[z] равно key[y]
17 // Копируем дополнительные данные связанные с y
18 Удалить y
Конец
Пример.
Пусть у нас есть дерево третьего порядка, с ключами 12, 8, 4, 9, 6, 13, 14, 16,100, 10.
Приходит ключ 12, его заносим в корень
12
П
8 12
риходит 8, 8 меньше 12
Приходит 4, места в корне нет, разбиваем на 2
Приходит 9, она больше 8, но меньше 12, 12 сдвигаем, перед ней записываем 9, приходит 6 она меньше 8, но больше 4, записываем ее после 4:
После того как придет 13, 14, 16, 100, 10 вид дерева будет следующим:
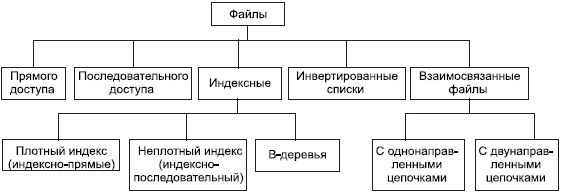
12. Методы прямого доступаФайловые структуры, используемые для хранения информации в базах данных В каждой СУБД по-разному организованы хранение и доступ к данным, однако существуют некоторые файловые структуры, которые имеют общепринятые способы организации и широко применяются практически во всех СУБД. В системах баз данных файлы и файловые структуры, которые используются для хранения информации во внешней памяти, можно классифицировать следующим образом (см. рис. 9.1).
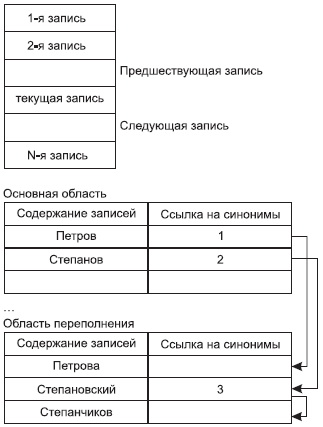
Рис. 9.1. Классификация файлов, используемых в системах баз данных С точки зрения пользователя, файлом называется поименованная линейная последовательность записей, расположенных на внешних носителях. На рис. 9.2 представлена такая условная последовательность записей. Так как файл — это линейная последовательность записей, то всегда в файле можно определить текущую запись, предшествующую ей и следующую за ней. Всегда существует понятие первой и последней записи файла Ф В этих файлах физический адрес расположения нужной записи может быть вычислен по номеру записи (NZ).
Рис. 9.2. Файл как линейная последовательность записей |
айлы
с постоянной длиной записи, расположенные
на устройствах прямого доступа (УПД),
являются файлами
прямого доступа.Основная идея, лежащая в основе организации файлов с хэшированным доступом заключается в разделении записей файла между участками, каждый из которых, содержит один или более блоков памяти. Для любого файла, хранимого таким образом, существует функция h, которая использует в качестве аргумента значение ключа файла и производит некоторое целое число от нуля до некоторого максимального значения.
Допустим V это значение ключа. Тогда h(V) указывает номер участка, в котором должна находится запись с этим значением ключа, если она присутствует вообще.
Необходимо, чтобы h хэшировала, т.е. чтобы h(V) принимала все ее возможные значения примерно с равной вероятностью, когда V пробегает по множеству значений ключа.
На данном ниже рисунке показана организация хэширования файла с B-участками.
Интерпретируем значения ключа как последовательность битов, формированную путем конкатенации значений всех полей ключа. Эта последовательность имеет фиксированную длину, поскольку каждое поле имеет фиксированную длину.
Делим последовательность битов на группы, состоящие из фиксированного числа битов, например 16-ти. Последнюю группу при необходимости дополняем нулями.
Складываем группу битов как целые числа.
Делим сумму на число участков и используем остаток как номер участка.
Н
а
рис. Показан справочник участков,
состоящий из
Поиск.
Предположим, что имеется значение V единственного поля ключа. В том случае, когда ключ состоит из нескольких полей, V является списком значений полей ключа в фиксированном порядке.
Вычислим h(V), которая даст нам номер участка, например i. Далее обращаемся в справочник и найдем первый блок участка i. После этого необходимо исследовать каждый блок участка и выяснить содержится ли в нем запись со значением ключа V.
Если да, то мы нашли нужную запись, если в блоках участка записи с таким значением ключа нет, то такой записи не сущетсвует.
Модификация.
Пусть необходимо модифицировать одно или более полей записи со значением ключа V. Интерпретируем эту модификацию как удаление и включение.
Включение.
Применяем процедуру поиска. Если запись с заданным значением ключа V найдена, то ошибка, так как такая запись уже есть. Если записи нет, то находим первый свободный субблок среди блоков участка h(V). Субблок – это часть блока куда помещаются записи. Адрес такого субблока можно запомнить при операции поиска. Помещаем запись в субблок. Если свободных субблоков нет, то делаем новый пустой блок, помещаем указатель на него в заголовок предыдущего блока, а в заголовок его самого помещаем null. После этого помещаем в него запись.
Удаление.
Ищем. Если записи нет, то ошибка. Далее устанавливаем в заголовке блока бит, означающий, что соответствующий ему субблок свободен. Однако если существуют указатели на удаленную запись, то кроме этого бита включается бит, говорящий, что запись была удалена. Таким образом, если на этоже место будет записана другая информация, то при обработке указателя на этот субблок мы увидим, что старая запись была удалена, что будет означать, что старый указатель больше не действителен.
Возможно дополнить механизм удаления так, чтобы блок, который окажется свободным после удаления также был удален.
Основным требование к хэш-функции является равномерное распределение значений свертки, где одному значению хэш-функция может соответствовать одно значение ключа. Если для нескольких значений ключа получается одно и то же значение хэш-функция – коллизия.
Значения ключей, которые имеют одно и то же значение хэш-функции – синонимы.
Методы разрешения коллизий
Метод последовательного перебора. Значение хэш-функции – отправная точка для дополнительного просмотра и поиска. Запись сохраняется в первом свободном месте.
Стратегия разрешения коллизий с областью переполнения. Область хранения разбивается на две части: основную и область переполнения. Значение хэш-функции – адрес записи, запись заносится в основную область. Если при вставке нового значения возникает коллизия, то новая запись заносится в область переполнения на первое свободное место, а записи-синониме в основной области делается ссылка на адрес вновь размешенной записи в области переполнения. Следующая новая запись-синоним будет располагаться на втором месте списка. Т. о. для размещения новой записи требуется не более двух обращений к диску. Хорошим результатом может считаться наличие не более 10 синонимов.
Организация стратегии свободного размещения. Одна общая область замещения. Записи-синонимы организуются в двухсвязный список.
Если при вставке новой записи ее адрес занят записью, которая не является заголовком списка, то она перемещается на свободное место с коррекцией указателей. А новая запись встает на ее место.
Если адрес занят заголовком списка, то новая запись располагается на свободном месте, и для нее устанавливаются соответствующие указатели.
Если адрес свободен, то новая запись размещается в заданном месте и становится заголовком в списке синонимов.