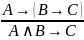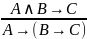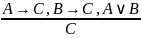- •0. Вопросы (указатель).
- •1. Язык логики высказываний. Простые высказывания, сложные высказывания, логические связки. Роль связок в естественном языке.
- •2. Синтаксис языка логики высказываний: алфавит и правила построения формул. Семантика языка логики высказываний, интерпретация формул.
- •3. Свойства формул: общезначимость, выполнимость, противоречивость, опровержимость.
- •4. Основные схемы логически правильных рассуждений.
- •5. Основные тавтологии, выражающие свойства логических операций.
- •6. Основные правила получения тавтологий.
- •7. Логическая равносильность формул. Алгоритм проверки логической равносильности формул. Свойства отношения равносильности на множестве формул. Равносильные преобразования.
- •8. Логическое следование формул. Логические следствия и посылки. Алгоритм проверки формул на логическое следование. Признаки логического следствия. Два свойства логического следования.
- •9. Следование и равносильность формул.
- •10. Нахождение следствия для данных посылок.
- •11. Нахождение посылок для данного следствия.
- •12. Алгебра логики. Функции алгебры логики. K-значные логики.
- •13. Способы задания функций алгебры логики. Единичные и нулевые наборы функций алгебры логики. Фиктивные (несущественные) переменные.
- •14. Бинарные функции алгебры логики.
- •15. Суперпозиции и формулы. Глубина формулы. Способы записи формул.
- •16. Эквивалентные формулы. Способы установления эквивалентности формул.
- •17. Полнота и замкнутость системы функций. Функционально полные базисы. Классы Поста. Теорема Поста о полноте системы булевых функций.
- •18. Булева алгебра логических операций. Основные эквивалентные соотношения (законы) в булевой алгебре.
- •19. Разложение функций по переменным. Совершенная дизъюнктивная нормальная форма.
- •20. Днф, сднф, кнф, скнф. Процедуры приведения к днф и кнф.
- •2 1. Двойственность.
- •22. Алгебра Вебба, алгебра Шеффера, импликативная алгебра, коимпликативная алгебра, алгебра Жегалкина.
- •23. Полиномы Жегалкина. Процедуры приведения к пнф.
- •24. Конечно-значные логики: алгебра Вебба, алгебра Поста, алгебра Россера–Тьюкетта.
- •25. Исчисление высказываний как формальная система, множественность аксиоматизаций. Проблема выводимости. Прямой вывод.
- •26. Теорема дедукции. Связь выводимости и истинности формул в логике высказываний. Выполнимые и общезначимые формулы.
- •27. Понятие логического следования, принцип дедукции. Правило резолюций, метод резолюций. Стратегии метода резолюций.
- •29. Алгоритм построения резолюций для множества фраз Хорна.
- •30. Свойства формализованного счисления высказываний.
- •31. Предикат. Предикаты и отношения. Предикаты и функции. Предикаты и высказывания.
- •32. Синтаксис языка логики предикатов: алфавит, термы, атомы, правила построения формул.
- •33. Кванторные операции. Свободные и связанные вхождения переменных. Логический квадрат.
- •34. Численные кванторы. Ограниченные кванторы.
- •35. Множество истинности предикатов. Равносильность и следование предикатов.
- •37. Приведенная нормальная форма. Процедура получения приведенной нормальной формы.
- •38. Предваренная нормальная форма. Процедура получения предваренной нормальной формы.
- •39. Проблема разрешимости для общезначимости и выполнимости формул логики предикатов. Теорема Черча. Частные случаи.
- •40. Методы доказательства в логике предикатов.
- •41. Исчисление предикатов как формальная система. Формальный вывод в исчислении предикатов. Правило переименования свободных переменных. Правило переименования связанных переменных.
- •42. Выводимость и истинность в логике предикатов. Эквивалентные преобразования.
- •43. Предваренная, сколемовская и клаузальная формы. Алгоритм получения клаузальной формы.
- •45. Принцип логического программирования.
- •46. Применение логики предикатов в логико-математической практике.
- •47. Классификация высказываний по Аристотелю.
- •48. Методы рассуждений. Аристотелева силлогистика. Теоретико-множественная интерпретация аристотелевой силлогистики
- •49. Принцип полной дизъюнкции в предикатной форме
- •50. Метод (полной) математической индукции.
- •51. Необходимые и достаточные условия
- •52. Понятия формальной системы и формального вывода. Аксиоматическая (формальная) теория и принципы ее построения.
- •53. Вывод и выводимость в формальной теории. Разрешимые и неразрешимые формулы. Доказательство и доказуемость. Теорема формальной теории.
- •54. Основные свойства формальных систем: непротиворечивость, полнота, разрешимость. Полнота и непротиворечивость исчисления высказываний. Полнота и непротиворечивость исчисления предикатов.
- •55. Прикладные исчисления предикатов. Формальная арифметика. Теорема Генцена о непротиворечивости формальной арифметики.
- •56. Теоремы о неполноте формальных систем, смысл и значение теорем Геделя для практической информатики.
- •57. Неклассические логики.
- •58. Интуиционистская логика.
- •59. Нечеткая логика.
- •60. Модальные логики. Типы модальностей.
- •61. Временные логики. Приложение временных логик к программированию.
- •62. Алгоритмические логики. Принципы построения алгоритмической логики. Алгоритмическая логика Хоара.
- •63. Многозначные логики. Трёхзначная логика я.Лукасевича. M-значная логика э.Поста.
- •64. Предпосылки возникновения теории алгоритмов. Основные требования к алгоритмам. Подходы к уточнению понятия «алгоритм». Три основных типа универсальных алгоритмических моделей.
- •65. Машина Тьюринга. Конфигурация машины Тьюринга. Функция, правильно вычислимая по Тьюрингу. Эквивалентные машины Тьюринга. Композиция машин Тьюринга.
- •66. Вычисление предикатов на машине Тьюринга.
- •67. Универсальная машина Тьюринга. План построения универсальной машины Тьюринга.
- •68. Тезис Тьюринга.
- •69. Проблема остановки как пример алгоритмически неразрешимых проблем.
- •70. Машина Поста.
- •71. Рекурсивные функции. Примитивно-рекурсивные функции. Примитивно-рекурсивные операторы. Частично-рекурсивные функции. Тезис Черча.
- •72. Нормальные алгорифмы Маркова. Нормально вычислимые функции и принцип нормализации Маркова.
- •73. Вычислимость и разрешимость. Нумерация алгоритмов. Алгоритмически разрешимые и неразрешимые задачи. Проблема остановки, проблема самоприменимости, проблема пустой ленты.
- •74. Требование результативности и теория алгоритмов.
- •75. Разрешимые и перечислимые множества. Связь между разрешимостью и перечислимостью множеств. Теорема Райса.
- •76. Сложность алгоритмов. Меры сложности алгоритмов. Сложность задачи. Массовые и индивидуальные задачи.
- •77. Асимптотическая сложность, порядок сложности. Сложность в среднем и в худшем случае.
- •78. Трудоемкость алгоритмов. Классификация алгоритмов по виду функции трудоёмкости
- •79. Методики перехода к временным оценкам трудоёмкости алгоритмов. Пооперационный анализ. Метод Гиббсона. Метод прямого определения среднего времени.
- •1) Пооперационный анализ
- •2) Метод Гиббсона
- •3) Метод прямого определения среднего времени
- •80. Сложность и кодирование. Сложность и архитектура машины.
- •81. Полиномиальный алгоритм. Легко- и трудноразрешимые задачи, классы задач p и np.
- •82. Полиномиальная сводимость и np-полнота. Np-полные задачи. Примеры np-полных задач. Теорема Кука. Примеры практически значимых np-полных задач.
3. Свойства формул: общезначимость, выполнимость, противоречивость, опровержимость.
Общезначимая
формула (тавтология, тождественно
истинная) — истинная в любой интерпретации
(всегда истинная, при любых
наборах значений).
Обозначается |=а. Пример:
формула
 при любых значениях
при любых значениях
 .
.
Противоречивая формула (невыполнимая, тождественно ложная) — ложная в любой интерпретации (всегда ложная, при любых наборах значений).
Выполнимая формула (непротиворечивая, опровержимая) — не являющаяся противоречивой (не всегда ложная, не всегда истинная), может быть опровергнута.
4. Основные схемы логически правильных рассуждений.
В правильном рассуждении заключение вытекает из посылок с логической необходимостью, общая схема такого рассуждения выражает логический закон.
Логическая необходимость — тип логики, при котором для существования одного логического объекта необходимо существование другого. #: «Чтобы что-то купить, нужно иметь деньги».
Рассуждать логически правильно — рассуждать в соответствии с законами логики.
Логика не просто перечисляет некоторые схемы правильного рассуждения. Она выявляет различные типы таких схем, устанавливает общие критерии их правильности, выделяет исходные схемы, из которых по определенным правилам мб получены другие схемы (данного типа), исследует проблему взаимной совместимости схем и т. д.
1. |
Правило заключения — утверждающий модус Modus Ponens |
«Если из
следует
|
|
#: «Если лед нагревается, он тает. Лед нагревается. Значит он тает». |
|||
2. |
Правило отрицания — отрицательный модус Modus Tollens |
«Если из следует , но неверно, то неверно и ». |
|
3. |
Правило отрицания–утверждения Modus Tollen–Ponens |
«Если истинно или , или , и истинно одно из них, то другое ложно». |
|
4. |
Правило отрицания–утверждения Modus Tollen–Ponens |
«Если истинно или , или , и неверно одно из них, то истинно другое». |
|
«Если истинно A или B, и неверно одно из них, то истинно другое». |
|
||
5. |
Правило транзитивности (упрощенное правило силлогизма) |
«Если из
следует
,
и из
следует
|
|
6. |
Закон противоречия |
«Если из
следует
и
|
|
7. |
Правило контрапозиции |
«Если из следует , то из того, что неверно , следует, что неверно ». |
|
8. |
Правило сложной контрапозиции |
«Если из
и
следует
,
то из
и
|
|
9. |
Правило сечения |
«Если из A следует B, а из В и С следует D, то из А и С следует D». |
|
10. |
Правило импортации (правило объединения посылок) |
«Если из
|
|
11. |
Правило экспортации (правило разъединения посылок) |
«Если из и следует , то из следует , из которого следует ». |
|
12. |
Правило дилемм |
«Из следует , из следует , или , то ». |
|
5, 6, 7

 ,
и
истинно (справедливо),
то
тоже истинно».
,
и
истинно (справедливо),
то
тоже истинно».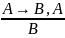

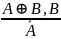 ,
,
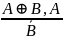 .
. ,
,
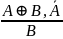 .
.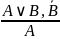 ,
,
 .
.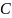 ,
то из
следует
».
,
то из
следует
».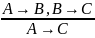
 ,
то неверно
».
,
то неверно
».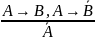
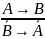
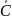 следует
».
следует
».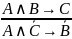

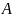 следует
следует
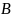 ,
из которого следует
,
из которого следует
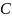 ,
то из
и
следует
».
,
то из
и
следует
».