50. Метод (полной) математической индукции.

Специальный метод, применяемый для доказательства истинности утверждений типа ("x Î N)(P(x)), т.е. ("x) (x Î N ® P(x)). Такие утверждения выражают тот факт, что некоторое свойство P присуще каждому натуральному числу.

Формальная основа — аксиома индукции, выражающая свойства естественного отношения порядка, имеющегося на множестве всех натуральных чисел.

Если свойством P обладает число 1 и для всякого натурального числа из того, что оно обладает этим свойством, следует, что и непосредственно следующее за ним натуральное число также обладает им, то и всякое натуральное число обладает свойством P.

Символически: (P(1) Ù ("x) (P(x) ® P(x+1))) ®("y)(P(y)).

Логическая схема доказательства методом математической индукции:

(1) P(1) — устанавливается проверкой; (2) ("x) (P(x) ® P(x+1)) — доказывается;

(3) P(1) Ù ("x) (P(x) ® P(x+1)) — из (1) и (2) по правилу введения конъюнкции;

(4) (P(1) Ù ("x)(P(x) ® P(x+1))) ®("y)(P(y)) — аксиома индукции; (5) ("y)(P(y)) — из (3) и (4) по МР.

P(1) — основание индукции;

предположение об истинности P(x) — предположение индукции;

доказательство истинности P(x+1) — шаг индукции.

51. Необходимые и достаточные условия

Пусть некоторая теорема имеет вид

("x) (P(x) ® Q(x)). Это означает, что предикат P(x) ® Q(x) тождественно истинен, т.е. его множество истинности (P® Q)⁺ = U =(Ø P)⁺ È Q⁺ . Следовательно, P⁺ Í Q⁺, а значит предикат Q(x) является следствием предиката P(x).

("x) (P(x) ® Q(x)) означает, что условие P(x) является достаточным для Q(x), а Q(x) — необходимым для P(x).

52. Понятия формальной системы и формального вывода. Аксиоматическая (формальная) теория и принципы ее построения.

Формальная система (ФС, формальная теория, аксиоматическая теория) — результат строгой формализации теории, предполагающей полную абстракцию от смысла слов используемого языка. Все условия, регулирующие употребление этих слов в теории, явно опред. аксиомами и правилами, позволяющими вывести одну фразу из других.

Формальный вывод — конечное упорядоченное множество строк, написанных на формальном языке, таких, что каждая из них либо является аксиомой, либо получена из предыдущих строк применением одного из правил вывода.

Формальная теория состоит из:

1. Множества знаков, образующих алфавит языка теории.

2. Множества слов, составленных из знаков алфавита, называемых формулами.

3. Подмножества формул всего множества формул, называемых аксиомами.

4. Множества правил вывода, с помощью которых из формул получают другие формулы.

Логическая аксиома — аксиома (схема) базовой логики, над которой надстраиваются конкретные теории за счет добавления новых аксиом, отражающих специфику теории. Последние называют нелогическими аксиомами.

53, 54

53. Вывод и выводимость в формальной теории. Разрешимые и неразрешимые формулы. Доказательство и доказуемость. Теорема формальной теории.

Формальная теория — способ изложения логики без учета семантики ПП, предикатов и формул. По замыслу создателей формальных теорий (#, Гильберт) таким образом можно избежать многих неприятностей, возникающих при использовании в логике человеческого языка, допускающего двусмысленность, недосказанность, переиначивание исходного значения, смысла и т.д.

Формальная теория состоит из:

1. Множества знаков, образующих алфавит языка теории.

2. Множества слов, составленных из знаков алфавита, называемых формулами.

3. Подмножества формул всего множества формул, называемых аксиомами.

4. Множества правил вывода, с помощью которых из формул получают другие формулы.

Логическая аксиома — аксиома (схема) базовой логики, над которой надстраиваются конкретные теории за счет добавления новых аксиом, отражающих специфику теории. Последние называют нелогическими аксиомами.

Пусть — формулы теории. Если существует такое правило вывода , что ( ) принадлежит , то говорят, что непосредственно выводима из по правилу вывода . ( — посылки, — заключение).

Выводом формулы из формул в формальной теории называется такая последовательность формул , что , а любая другая либо является аксиомой, либо исходной формулой, либо непосредственно выводима из ранее полученных формул. Если выводима из в теории , то — гипотезы. Теорема (доказуемая формула?) — формула, выводимая только из аксиом, без гипотез.

Формальное доказательство формулы в теории — конечная последовательность формул

, где каждая формула является либо аксиомой, либо получена из предыдущих с помощью одного из правил вывода, а 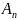— формула .

Последняя формула в доказательстве называется теоремой. Используется символическая запись для теорем:

( читается как «доказуемо » или « теорема». Знак введен в 1879 г. немецким логиком Готлобом Фреге).

Формальная теория разрешима, если существует алгоритм, который для любой формулы теории определяет, является лм эта формула теоремой теории.