2.3.9 Критический коэффициент сар. Критерий Гурвица
Под критическим (граничным) коэффициентом ККР системы автоматического регулирование понимается то значение коэффициента разомкнутой системы КРС , когда САР в замкнутом состоянии является нейтральной. Для определения значения критического коэффициента ККР системы можно использовать любой из критериев устойчивости. В данном случае рассмотрим использование критерия Гурвица для определения ККР.
Для этого необходимо воспользоваться характеристическим уравнением замкнутой системы:
Из коэффициентов уравнения составляется главный определитель Гурвица,
опираясь на следующие правила:
По главной диагонали определителя Гурвица располагаем коэффициенты характеристического уравнения, начиная с а1 ;
Столбцы определителя заполняются коэффициентами относительно главной диагонали : вверх с возрастающими, вниз - с убывающими индексами;
Вместо отсутствующих коэффициентов ставятся нули.
Остальные определители Гурвица составляются из главного определителя,
путем выделения количества строк (столбцов), равных порядковому номеру определителя.
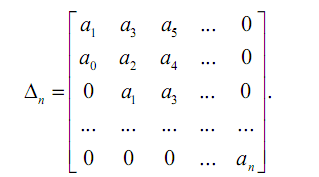
Для того чтобы система была устойчивой необходимо и достаточно чтобы
все определители Гурвица были положительными.
Если хотя бы один определитель меньше нуля, то система является неустойчивой.
И, если хотя бы один определитель равен нулю, а остальные больше нуля, то система является нейтральной.
Согласно последней формулировки, для определения значения критического коэффициента ККР системы достаточно воспользоваться предпоследним определителем, и приравняв его к нулю, находим значение ККР .
2.10 Построение области устойчивости в плоскости параметров системы
Использование критериев устойчивости не позволяет получить ответ: «В каких пределах можно варьировать параметры системы, сохранив ее устойчивость?».
Данную задачу решил Нейморк, и этот метод вошел в теорию автоматического управления, как: «Построение области устойчивости в плоскости параметров системы».
Метод является графоаналитическим и позволяет определить пределы варьирования одного или двух параметров системы.
Суть метода. Изменяя параметры системы в определенной последовательности, можно выбрать те комбинации параметров, когда корни характеристического уравнения системы являются нулевыми (расположены на оси ординат). На рис. 13 точки 1,2,3…m являются той комбинацией параметров M и N, когда хотя бы одна пара из корней характеристического уравнения системы (13) является мнимой. Соединив точки, получаем кривую, которая называется – кривая D-разбиения.
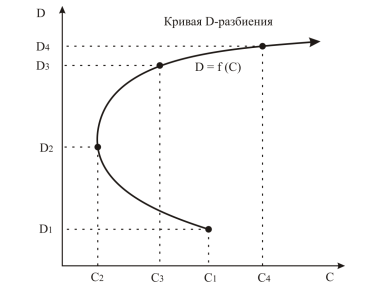
Рис. 13 Кривая D – разбиения в плоскости параметров C и D
Кривая D-разбиения разбивает плоскость параметров M и N на области с различным содержанием левых и правых корней. Та область, где все корни характеристического уравнения системы являются левыми, претендует на область устойчивости. Для выявления области устойчивости используется штриховка кривой D-разбиения. Исходным уравнением для построения область устойчивости является характеристического уравнения замкнутой системы, которое содержит варьируемые параметры M и N.
Рассмотрим алгоритм построения области устойчивости в плоскости одного
параметра системы N.
1. В характеристическом уравнении замкнутой системы выявляется варьируемый параметр N.
2. Выражается данное уравнение относительно варьируемого параметра N.
3. Переходя в
частотный диапазон, заменяя
, выделяя вещественную и мнимую
составляющие, получаем уравнение кривой
D-разбиения
.
4. Задавая частоту
до
, строим одну ветвь кривой D-разбиения
и при
до 0 – другую ветвь.
5. Нанося штриховку на ветви кривой D-разбиения, выделяем область устойчивости .
6. Из области устойчивости выбираем пределы варьирования параметра N.
7. Для выбранного значения N, и, используя любой критерий устойчивости,
выполняем проверку найденной области.