ГОУВПО «Воронежский государственный
технический университет»
Кафедра прикладной математики
400-2009
Методические указания
по высшей математике по теме
«Элементы теории вероятностей.
Случайные величины»
для студентов специальностей 160201
“Самолето- и вертолетостроение”,
130501 “Проектирование, сооружение
и эксплуатация газонефтепроводов
и газонефтехранилищ» очной формы обучения
Воронеж 2009
Составители: канд. физ.- мат. наук В.Н. Дурова,
канд. физ.- мат. наук М.И. Зайцева,
канд. физ.- мат. наук В.И. Кузнецова,
канд. техн. наук О.А. Соколова
УДК 517.2. (07)
Методические указания по высшей математике по теме
«Элементы теории вероятностей. Случайные величины» для студентов специальностей 160201 “Самолето- и вертолетостроение”, 130501 “Проектирование, сооружение и эксплуатация газонефтепроводов и газонефтехранилищ” очной формы обучения / ГОУВПО «Воронежский государственный технический университет»; сост. В.Н. Дурова, М.И. Зайцева, В.И. Кузнецова, О.А. Соколова. Воронеж, 2009. 48 с.
Методические указания содержат краткий теоретический материал и большое количество подробно разобранных задач, задачи для самостоятельного решения.
Предназначены для практических занятий на втором курсе.
Ил. 8. Библиогр.: 4 назв.
Рецензент д-р техн. наук, проф. М.Л. Лапшина
Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. В.Д. Репников
Печатается по решению редакционно-издательского совета Воронежского государственного технического университета
© ГОУВПО «Воронежский государственный
технический университет», 2009
Введение
Данные методические указания предназначены для проведения практических занятий по теме «Элементы тории вероятностей. Случайные величины». С целью облегчения самостоятельной работы студентов приводится большое количество подробно рассмотренных примеров для каждого занятия. Указания содержат варианты заданий для типовых расчетов.
Перед каждым практическим занятием следует изучить соответствующий материал по учебнику (или конспекту лекций) и ответить на относящиеся к занятию теоретические вопросы.
Занятие 1. Случайные величины. Виды случайных величин. Задание дискретной случайной величины.
Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед не известное и зависящее от случайных причин, которые заранее не могут быть учтены.
Дискретной (прерывной) называют случайную величину, которая принимает отдельные, изолированные возможные значения с определенными вероятностями. Число возможных значений дискретной случайной величины может быть конечным или бесконечным.
Законом распределения дискретной случайной величины называют соответствие между возможными значениями и их вероятностями; его можно задать таблично, аналитически (в виде формулы) и графически.
При табличном задании закона распределения дискретной случайной величины первая строка таблицы содержит возможные значения, а вторая — их вероятности:
х xl х2 . . . хп
р р1 р2 рп
Пример 1.1. В денежной лотерее выпущено 100 билетов. Разыгрывается один выигрыш в 50 руб. и десять выигрышей по 1 руб. Найти закон распределения случайной величины X — стоимости возможного выигрыша для владельца одного лотерейного билета.
Решение. Напишем возможные значения X: х1 = 0, x2= 1, х3 = 50. Вероятности этих возможных значений таковы:
р1 = 0,01. р2 = 0,1, p3= l-(p1 + p2) = 0.89.
Тогда искомый закон распределения
-
X
0
1
50
P
0,89
0,1
0,01
Контроль: 0,01+0,1+0,89=1.
Для наглядности закон распределения дискретной случайной величины можно изобразить и графически, для чего в прямоугольной системе координат строят точки (xi, рi), а затем соединяют их отрезками прямых. Полученную фигуру называют многоугольником распределения.
Пример 1.2. По мишени сделано 3 выстрела. Вероятность попадания при каждом выстреле равна р=0,6. За каждое попадание стрелку засчитывается по 5 очков. Построить ряд и многоугольник распределения случайной величины Х - числа выбитых очков.
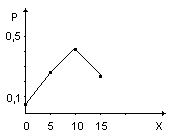Решение.
Случайная величина принимает значения:
0, 5, 10, 15. Соответствующие вероятности
Р(х=0)
=(1-р)3=0,064; Р(х=1)=
(0,6)1(0,4)2=
=3∙0,6∙0,16=0,288
Р(х=2)=
(0,6)2(0,4)1=0,432;
Рис.1 Р(х=3)=(0,6)3=0,216
Х |
0 |
5 |
10 |
15 |
Р |
0,064 |
0,288 |
0,432 |
0,216 |