Міністерство освіти науки молоді та спорту України

Національний університет „Львівська політехніка”

Інститут Комп’ютерних Технологій, Автоматики та Метрології

Кафедра КСА

Розрахункова робота з дисципліни:

«Конструювання, технологія виробництва та надійність засобів автоматики»

Номер залікової книжки: 1009253

Виконав: ст.гр.СІ-32

Довбенчук О.Т.

Перевірив:

Мокренко П.В.

Львів 2013

Завдання №1 (варіант 3)

Експоненціальний розподіл використовується в теорії надійності.

В загальному випадку записується:

P(x)= e^-λx

P(x)-імовірність того, що випадкова величина X має значення більше x.

Коли замість випадкової величини приймається час t то закон записується так:

P(t)=exp .

P(t)- імовірність безвідмовної роботи.

λ-інтенсивність відмов

Імовірність відмов за час t:

Q(t)=1-P(t)=1- e^-λt

Функція розподілу випадкових величин:

f(t)=λ e^-λt

Середній час роботи до виникнення відмов:

T₁=1/λ

Дисперсія:

D(t)=1/λ²

Середнє квадратичне відхилення за час t:

σ(t)=T₁

Криві розподілу: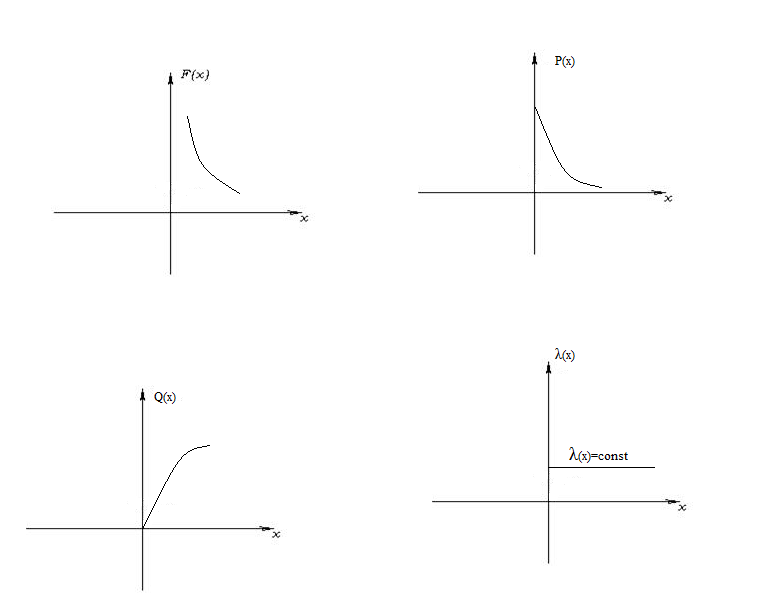

Завдання №2 (Варіант 3)

Непоновлювана система телевимірювання має експоненціальний закон розподілу часу безвідмовної роботи з інтенсивністю відмов λ. Визначити кількісні характеристики надійності для часу t₀.

Дано:

λ=10^-6 (1/год) Система має експоненційний закон розподілу, тому:

t₀=10⁵(год) 1.) Ймовірність безвідмовної роботи:

Р(t₀) – ?

Q(t₀) ­­– ? 2.) Вірогідність відмов за час t :

Т­­_сер– ? Q(t₀)=1– Р(t) =1–0.9=0.1

D(t₀) – ? 3.) Середній час роботи до виникнення відмов:

r(t₀) – ? Т­­_сер=1/λ=1/10^–6=10⁶ (год)

4.) Дисперсія часу роботи до виникнення відмови:

D(t₀)=1/λ²=1/(10^–6)²=1/10^–12=10¹² (год²)

5.) Середньоквадратичне відхилення часу роботи:

r(t₀)=Т­­_сер=1/λ=1/10^-6=10⁶ (год)

Відповідь: Р(t₀) =0.9 ; Q(t₀) =0.1 ; Т­­_сер=10⁶ (год) ; D(t₀) =10¹² (год²) ;

r(t₀)=10⁶ (год).

Обрахувавши кількісні характеристики надійності для часу 10⁵год не поновлюваної системи можна зробити висновок, що ймовірність того, що система перестане працювати значно більша ніж ймовірність безвідмовної роботи.

Завдання №3 (варіант 5)

Визначити ймовірність безвідмовної роботи тригера за t годин роботи, якщо інтенсивність відмов всіх елементів схеми постійні і дорівнюють відповідно: λ_Rк; λ_R; λ_Rs ; λ_С ; λ_T ; а відмова будь–якого з них веде до відмови тригера.

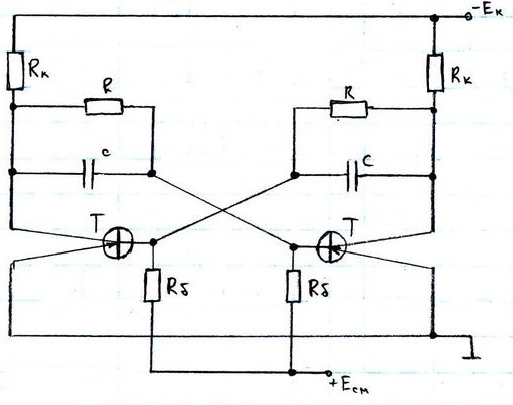Структурна схема з’єднання елементів по надійності:

2ΛRк 2λR 2λС 2λRs 2λT Дано:

λ_Rк=0.6· 10^–6(1/год.)

λ_R=0.5· 10^–6(1/год.)

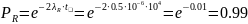
λ_С=0.6· 10^–6(1/год.)

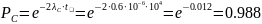
λ_Rs=0.26· 10^–6(1/год.)

λ_T=1,3· 10^–6(1/год.)

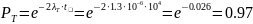
t =10⁴(год.) Р=

P(t)-?

Р_Rк(t)­–?

Р_R(t)­–?

Р_С(t)­–?

Р_Rs(t)­–?

Р_Т(t)­–?

Відповідь: Ймовірність безвідмовної роботи тригера дорівнює 0.932.

Завдання №4 (варіант 3)

Передавач телевимірювальної системи складається з чотирьох блоків. Перший блок включає в себе а₁ транзисторних комірок, другий - а₂, третій - а₃, четвертий - а₄ транзисторних комірок. Кожна транзисторна комірка може бути прийнята за деякий умовний елемент. Ймовірність безвідмовної роботи апаратури повинна бути рівна Р₀. Визначити ймовірність безвідмовної роботи окремих блоків системи Р_і і дати висновок.

Д ано:

Р₀=0,95 Ймовірність безвідмовної роботи і–того блоку матиме наступний

а₁=8 вигляд: Р_і=e^–Аі , де

а₂=12 А_і– показник ненадійності апаратури

а₃=18 1.) Знаходимо показник ненадійності апаратури:

а ₄=22 А= –lnР₀= – ln0,95=0,051

Р_і–? 2.) Знаходимо сумарну кількість елементів апаратури:

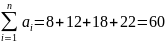
3.) Знаходимо показник ненадійності кожного блоку А_і:

8

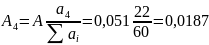
4.) Знаходимо ймовірність безвідмовної роботи для кожного блоку:

Р₁=e^–0,0068=0.993

Р₂=e^–0,0102=0,990

Р₃=e^–0,0153=0,985

Р₄=e^–0,0187=0,981

Зробимо перевірку:

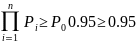
Відповідь: Р_і=0.95.

Завдання №5 (варіант 3)

Цифровий вимірювач часових інтервалів складається із трьох блоків: генератора еталонних імпульсів, управляючого пристрою та лічильника. Визначити ймовірність безвідмовної роботи цифрового вимірювача за час t, якщо час безвідмовної роботи генератора підпорядковується закону Вейбула з параметрами розподілу x₀, К ; а управляючий пристрій та лічильник – експоненційному закону з інтенсивністю відмов λ_кп та λ_лі відповідно.

Д ано:

x₀=40·10⁶ Структурна схема пристрою:

К

Г

КП

ЛІ

=3 λ₀λ_кпλ_лі

λ _кп =400·10^–6 (1/год.) П ПУ Л1

λ_лі=200·10^–6 (1/год.)

t =10³ (год.) 1.) Знаходимо: х₀=1/λ₀ , отже:

Р(t) – ? λ₀=1/х₀=1/40·10⁶=0,025 ·10⁶ (1/год.)

2.) Знаходимо ймовірність відмов генератора:

3.) Знаходимо ймовірність безвідмовної роботи пристрою управління та лічильника.

Р_ПУ(t)=

Р_ЛІ(t)=

4.) Знаходимо ймовірність безвідмовної роботи. Оскільки всі пристрої задані послідовно, то:

Р(t)= ·Р_ПУ(t)·Р_ЛІ(t)=0,975·0,961·0,980=0,918

Відповідь: Ймовірність безвідмовної роботи системи рівний 0,918.

Завдання №6 (варіант 5)

Відновлювана комп’ютеризована система управління має наступні результати вимірювань часу напрацювання на відмову:

№ відмов	1	2	3	4	5	6	7	8	9	10
tні(год.)	11	9,0	8,0	5,5	9,2	6,3	4,2	0,5	1,0	0,2

деt_ні(год.)– час роботи між сусідніми відмовами

Час поновлення є випадковою величиною, що приймається з ймовірністю Р_і значення t_П1 та Р₂ значення t_П2. Визначити коефіцієнт готовності системи.

Д ано:

Р₁=0,6 Коефіцієнт готовності визначаємо як відношення середнього

Р₂=0,4 часу наробітку безвідмовної роботи (Т_н) до суми Т_н+Т_п

t_в1=0,2 час поновлення.

t_в2=3,5

t =10³ (год)

К_г – ? Час наробітку безвідмовної роботи визначається як:

(год.)

Час поновлення визначаємо за формулою:

Т_п=Р₁·t_в1+Р₂·t_в2=0,6·0,2+0,4·3,5=1,52 (год)

Відповідь: Коефіцієнт готовності системи рівний 0,783

Завдання №7 (варіант 5)

Визначити ймовірність відмови комп’ютеризованої системи автоматики і управління за час t, якщо відомо, що час до відмови підпорядковується нормальному розподілу за часом Т.

Д ано:

t=610 (год)

Т=530 (год) ;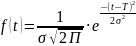

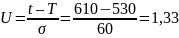
σ (t)=60

Q (t)=?

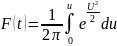
F(t)=0,413 – значення нормальної функції розподілу.

F(t)=0,5+Φ(U), звідси Φ(U)=F(t)–0,5

Ймовірність відмови системи телемеханіки за час t:

Q(t) = 0,5+Φ(U) Q(t)=0,5+F(t)–0,5=F(t)

Отже Q(t) = 0,413

Відповідь: ймовірність відмови системи дорівнює 0,413.