5. Задачи решаемые сэвм. Классификация сэвм по областям применения. Специализация центральных, периферийных устройств и программного обеспечения эвм. Сэвм для решения задач моделирования.

Задачи:

1. Экономические

2. Инженерно-технические

3. Управления

4. Моделирования

Хотя производительность ВС общего назначения неуклонно возрастает, по-прежнему остаются задачи, требующие существенно большей вычислительной мощности. К таким, прежде всего, следует отнести задачи моделирования реальных процессов и объектов, для которых характерна обработка больших регулярных массивов чисел в форме с плавающей запятой. Такие массивы представляются матрицами и векторами, а алгоритмы их обработки описываются в терминах матричных операций. Как известно, основные матричные операции сводятся к однотипным действиям над парами элементов исходных матриц, которые, чаще всего, можно производить параллельно. В универсальных ВС, ориентированных на скалярные операции, обработка матриц выполняется поэлементно и последовательно. При большой размерности массивов последовательная обработка элементов матриц занимает слишком много времени, что и приводит к неэффективности универсальных ВС для рассматриваемого класса задач. Для обработки массивов требуются вычислительные средства, позволяющие с помощью единой команды производить действие сразу над всеми элементами массивов — средства векторной обработки.

Под вектором понимается одномерный массив однотипных данных (обычно в форме с плавающей запятой), регулярным образом размещенных в памяти ВС. Если обработке подвергаются многомерные массивы, их также рассматривают как векторы.

При размещении матрицы в памяти все ее элементы заносятся в ячейки с последовательными адресами, причем данные могут быть записаны строка за строкой или столбец за столбцом (рис. 13.3). С учетом такого размещения многомерных массивов в памяти вполне допустимо рассматривать их как векторы и ориентировать соответствующие вычислительные средства на обработку одномерных массивов данных (векторов).

Так, если рассмотренная в примере матрица расположена в памяти построчно, адреса последовательных элементов строки различаются на единицу, а для элементов столбца шаг равен пяти. При размещении матрицы по столбцам единице будет равен шаг по столбцу, а шаг по строке — четырем. В векторной концепции для обозначения шага, с которым элементы вектора извлекаются из памяти, применяют термин шаг по индексу (stride).

Еще одной характеристикой вектора является число составляющих его элементов — длина вектора.

Векторный процессор — это процессор, в котором операндами некоторых команд могут выступать упорядоченные массивы данных — векторы. Векторный процессор может быть реализован в двух вариантах. В первом он представляет собой дополнительный блок к универсальной вычислительной машине (системе). Во втором — векторный процессор — это основа самостоятельной ВС.

Рассмотрим возможные подходы к архитектуре средств векторной обработки. Наиболее распространенные из них сводятся к трем группам:

1. конвейерное АЛУ;

2. массив АЛУ;

3. массив процессорных элементов.

Последний вариант — один из случаев многопроцессорной системы, известной как матричная ВС Понятие векторного процессора имеет отношение к двум первым группам, причем, как правило, к первой. Эти две категории иллюстрирует рис. 13.4 [200].

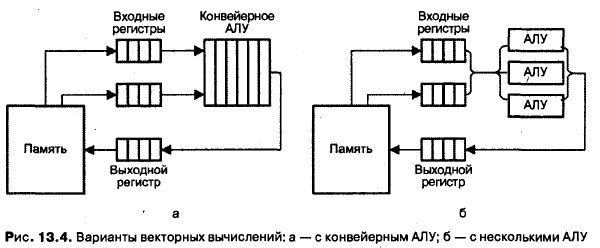
В варианте с конвейерным АЛУ (рис. 13.4, а) обработка элементов векторов производится конвейерным АЛУ для чисел с плавающей запятой (ПЗ). Операции с числами в форме с ПЗ достаточно сложны, но поддаются разбиению на отдельные шаги. Так, сложение двух чисел может быть сведено к четырем этапам:

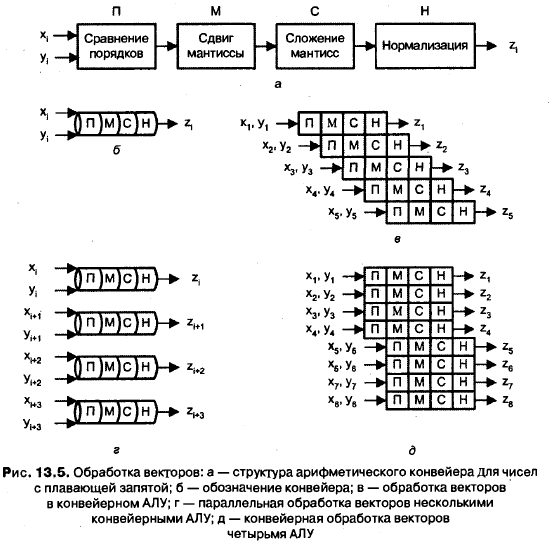
сравнению порядков, сдвигу мантиссы меньшего из чисел, сложению мантисс и нормализации результата (рис. 13.5, а). Каждый этап может быть реализован с помощью отдельной ступени конвейерного АЛУ (рис. 13.5, б). Очередной элемент вектора подается на вход конвейера, как только освобождается первая ступень (рис. 13.5, в). Ясно, что такой вариант вполне годится для обработки векторов.

Одновременные операции над элементами векторов можно проводить и с помощью нескольких параллельно используемых АЛУ, каждое из которых отвечает за одну пару элементов (см. рис. 13.4, б). Такого рода обработка, когда каждое из АЛУ является конвейерным, показана на рис. 13.5, г.

Если параллельно используются конвейерные АЛУ, то возможен еще один уровень конвейеризации, что иллюстрирует рис. 13.5, д. Вычислительные системы, где реализована эта идея, называют векторно-конвейерными. Коммерческие векторно-конвейерные ВС, в состав которых для обеспечения также скалярный процессор, известны как суперЭВМ.

Структура векторного процессора

Обобщенная структура векторного процессора приведена на рис. 13.6. На схеме показаны основные узлы процессора, без детализации некоторых связей между ними.

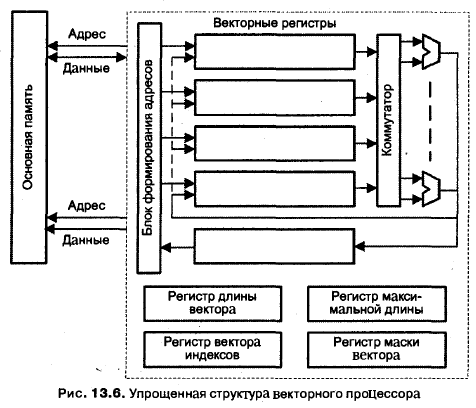
Обработка всех п компонентов векторов-операндов задается одной векторной командой. Общепринято, что элементы векторов представляются числами в форме с плавающей запятой (ПЗ). АЛУ векторного процессора может быть реализовано в виде единого конвейерного устройства, способного выполнять все предусмотренные операции над числами с ПЗ. Более распространена, однако, иная

структура, — в ней АЛУ состоит из отдельных блоков сложения и умножения, а иногда и блока для вычисления обратной величины, когда операция деления X/Y реализуется в виде X (1/Y) Каждый из таких блоков также конвейеризирован.

Кроме того, в состав векторной вычислительной системы обычно включают и скалярный процессор, что позволяет параллельно выполнять векторные и скалярные команды.

Для хранения векторов-операндов вместо множества скалярных регистров используют так называемые векторные регистры, которые представляют собой совокупность скалярных регистров, объединенных в очередь типа FIFO, способную хранить 50-100 чисел с плавающей запятой. Набор векторных регистров (Vc,Vb,Vc,….) имеется в любом векторным процессоре. Система команд векторного процессора поддерживает работу с векторными регистрами и обязательно включает в себя команды:

загрузки векторного регистра содержимым последовательных ячеек памяти, указанных адресом первой ячейки этой последовательности;

выполнения операций над всеми элементами векторов, находящихся в векторных регистрах;

сохранения содержимого векторного регистра в последовательности ячеек памяти, указанных адресом первой ячейки этой последовательности.

В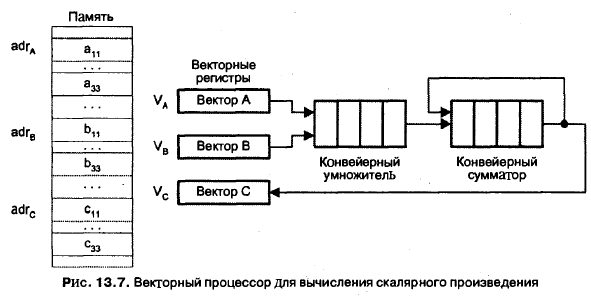 екто рный процессор с конвейеризированными блоками обработки для вычисления скалярного произведения показан на рис. 13.7.

Важным элементом любого векторного процессора (ВП) является регистр длины вектора. Этот регистр определяет, сколько элементов фактически содержит обрабатываемый в данный момент вектор, то есть сколько индивидуальных операций с элементами нужно сделать. В некоторых ВП присутствует также регистр максимальной длины вектора, определяющий максимальное число элементов вектора, которое может быть одновременно обработано аппаратурой процессора. Этот регистр используется при разделении очень длинных векторов на сегменты, длина которых соответствует максимальному числу элементов, обрабатываемых аппаратурой за один прием.

Достаточно часто приходится выполнять такие операции, в которых должны участвовать не все элементы векторов. Векторный процессор обеспечивает данный режим с помощью регистра маски вектора. В этом регистре каждому элементу вектора соответствует один бит. Установка бита в единицу разрешает запись соответствующего элемента вектора результата в выходной векторный регистр, а сброс в ноль — запрещает.

10. Цифровые интегрирующие вычислительные машины и системы. Симметричная система дифференциальных уравнений К.Шеннона. Методы перехода от произвольной математической зависимости к порождающим системам дифференциальных уравнений К.Шеннона.

На основе разностной СУШ могут быть построены различные типы цифровых интегрирующих машин: экстраполяционные и интерполяционные, последовательные и параллельные. Экстраполяционные параллельные ЦИМ конструируются непосредственно на основе уравнений разностной СУШ и в общем случае состоят из N реальных цифровых интеграторов, 2N сумматоров и N экстраполяторов приращений. Вычислительные блоки в подобных ЦИМ работают параллельно, в результате чего процесс интегрирования оказывается развернутым в пространстве и скорость интегрирования повышается по сравнению

с последовательными ЦИМ в N раз. В структуру параллельных ЦИМ входят: электронное коммутирую-

щее устройство (КУ), устройство управления, а также устройства ввода и вывода информации.

Последовательная экстраполяционная ЦИМ состоит в общем случае из одного интегратора, двух сумматоров и одного экстраполятора приращений, а также иногда из некоторых дополнительных решающих блоков, которые последовательно обрабатывают информацию, относящуюся к N различным интеграторам. В результате процесс интегрирования оказывается развернутым во времени. Последовательная ЦИМ должна содержать запоминающее устройство, в котором хранятся исходные и промежуточные данные для каждого решающего блока, а также программа решения задачи. Кроме того в структуру последовательной ЦИМ входят: простые устройства ввода и вывода информации. (Отдельные структурные компоненты последовательной ЦИМ используются в лабораторных работах при моделировании параллельной ВС.) Последовательные ЦИМ требуют меньших затрат оборудования, чем параллельные, но и скорость их работы в N раз меньше. Наряду с экстраполяционными ЦИМ могут быть сконструированы параллельные и последовательные интерполяционные ЦИМ с параллельным и последовательным способами обработки информации в цифровых интеграторах, отличающихся точностью формул численного интегрирования, и других решающих блоков, а так же по способу образования и использования приращений или значений приращений.

ПЕРЕХОД ОТ ФУНКЦИЙ К ПОРОЖДАЮЩИМ УРАВНЕНИЯМ ШЕННОНА.

Рассмотрим один из наиболее эффективных методов перехода от заданных функций к порождающим системам уравнений Шеннона. Допустим, что задана какая-либо негипетрансцендентная функция многих переменных

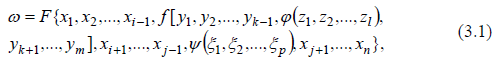
представляющая собой суперпозицию более простых функций, которую необходимо представить в форме уравнений Шеннона. Такую функцию следует прежде всего расчленить на ряд элементарных функций:

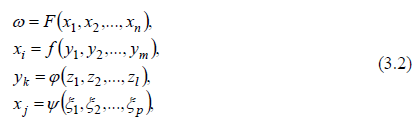
каждая из которых не поддается дальнейшему расчленению и упрощению на основе принципа суперпозиции. Затем для каждой функции из системы (3.2) необходимо составить порождающую систему уравнений Шеннона. Объединяя системы уравнений, определенные для каждой из функций (3.2), получим общую систему уравнений Шеннона, задающую исходную функцию.

Остается рассмотреть метод перехода от некоторой негипертрансцендентной функции

z = f (y1, y2 ,..., yl ), (3.3)

не поддающейся дальнейшему расчленению на более элементарные функции, к порождающей системе уравнений Шеннона. С этой целью продифференцируем функцию (3.3)

и введем обозначения

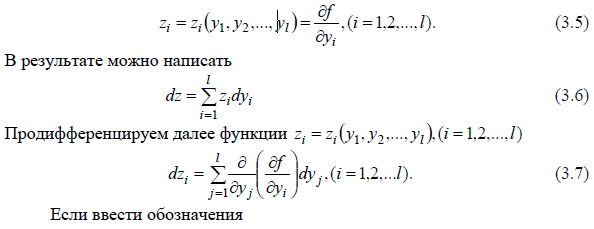
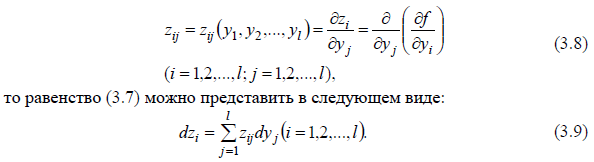
Продолжая процесс дифференцирования zi аналогичным образом и вводя соответствующие обозначения zij (подстановки) для возникающих при этом новых функций, получим систему дифференциальных уравнений. По условию функция z = f (y1, y2 ,..., yl) негипертрансцендентна и, следовательно, удовлетворяет конечной системе уравнений Шеннона. Любая функция может удовлетворять конечной системе дифференциальных уравнений только тогда, когда при последовательном дифференцировании указанной функции, начиная с некоторого шага дифференцирования, ее высшие частные производные либо обращаются в ноль, либо содержат периодически повторяющиеся функции. Таким образом, общая схема перехода от заданной функции к порождающей системе уравнений Шеннона состоит из следующих этапов: расчленение исходной функции с учетом суперпозиции на более простые; последовательное дифференцирование каждой простой функции (при одновременном введении новых переменных) до момента получения конечной системы уравнений Шеннона; и, наконец, определение начальных значений всех зависимых переменных, входящих в систему.