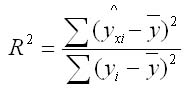Необходимое условие экстремума

      Функция g(x) в точке  имеет экстремум(максимум или минимум), если функция определена в двухсторонней окрестности точки и для всех точек x  некоторой области:  , выполнено соответственно неравенство

(в случае максимума) или  (в случае минимума).

Экстремум функции находиться из условия: , если производная существует, т.е. приравниваем первую производную функции к нулю.

20. Второе и третье достаточные условия экстремума.

2) Второе достаточное условие

     Если функция g(x) обладает второй производной  причем в некоторой точке первая производная равна нулю, а вторая производная отлично от нуля. Тогда точка экстремум функции g(x), причем если  , то точка является максимумом; если  , то точка является минимумом.

3) Третье достаточное условие

     Пусть функция g(x) имеет в некоторой окрестности точки   N производных, причем значение первых (N - 1)- ой и самой функции в этой точке равно нулю, а значение N-ой производной отлично от нуля. В таком случае:

а) Если N - четно, то точка   экстремум функции:  у функции точка максимума,    у функции точка минимума.

б) Если N - нечетно, то в точке  у функции g(x) экстремума нет.

21. Выпуклость и вогнутость графика функции. Достаточное условие выпуклости и вогнутости графика функции.

График функции y=f(x) называется выпуклым на интервале (a; b), если он расположен ниже любой своей касательной на этом интервале.

График функции y=f(x) называется вогнутым на интервале (a; b), если он расположен выше любой своей касательной на этом интервале.

Пусть y=f(x) дифференцируема на (a; b). Если во всех точках интервала (a; b) вторая производная функции y = f(x) отрицательная, т.е. f ''(x) < 0, то график функции на этом интервале выпуклый, если же f''(x) > 0 – вогнутый.

22. Точки перегиба. Необходимое условие перегиба. Критические точки второго рода.

Пусть кривая определяется уравнением y = f(x). Если f ''(x0) = 0 или f ''(x0) не существует и при переходе через значение x = x0 производная f ''(x) меняет знак, то точка графика функции с абсциссой x = x0 есть точка перегиба.

Точки перегиба следует искать только среди таких точек, где вторая производная обращается в нуль или не существует.

Необходимые условия наличия перегиба 

       либо   не существует.

Точка называется критической точкой второго рода, если

1. непрерывна в некоторой окрестности ;

2. существует (конечная или бесконечная) производная функции в точке ;

3. дважды дифференцируема в некоторой проколотой окрестности точки ;

4. вторая производная этой функции в точке равна нулю или не существует.

Критическая точка второго рода - это точка функции, в которой вторая производная функции равна 0.

В этой точке происходит перегиб, то есть график меняется с выпуклого вверх на выпуклый вниз, или наоборот.

23. Достаточные условия перегиба (3 условия).

Достаточные условия наличия перегиба 

     1. Если   меняет знак при переходе через точку x₀, то x₀ - точка перегиба.

2. Если   то при n четном x₀ - точка перегиба, при n нечетном x₀ не является точкой перегиба.

24. Схема исследование функции с помощью производной.

Сами же точки экстремума не принадлежат ни к интервалам возрастания, ни к интервалам убывания функции. Потому в точках экстремума производная не может быть ни положительной, ни отрицательной. Значит, в этих точках она или равна нулю, или ее не существует вообще.

25. Понятие первообразной функции. Понятие неопределенного интеграла.

Выражение вида   называется интегралом от функции f(x), где f(x) - подынтегральная функция, которая задается (известная), dx - дифференциал x, с символом  всегда присутствует dx.

Определение. Неопределенным интегралом  называется функция F(x) + C, содержащая произвольное постоянное C, дифференциал которой равенподынтегральному выражению f(x)dx, т.е.  или  Функцию   называют первообразной функции   . Первообразная функции   определяется с точностью до постоянной величины.

26. Основные свойства неопределенного интеграла, основные табличные интегралы (формулы).

27. Методы интегрирования (почленное интегрирование, внесение под знак дифференциала, замена переменной).

28. Предмет математической статистики и ее прикладное значение.

29. Статистические данные. Классификация признаков.

Единицы совокупности обладают определенными свойствами, качествами. Эти свойствапринято называть признаками. Например, признаки человека: возраст, образование, занятие,рост, вес, семейное положение и т.д.; признаки предприятия: форма собственности,специализация (отрасль), численность работников, величина уставного фонда, экономическаяэффективность его деятельности и т. д.

Статистика изучает явления через их признаки: чем более однородна совокупность, тем большеобщих признаков имеют ее единицы и меньше варьируют их значения.            

     Классификация признаков в статистике

Основная классификация
по характеру их выражения	по способуизмерения	по отношению кхарактеризуемомуобъекту	по характерувариации	по отношению ковремени
1. Описательные	1. Первичные илиучитываемые	1. Прямые(непосредственные)	1. Альтернативные	1. Моментные
2. Количественные	2. Вторичные илирасчетные	2. Косвенные	2. Дискретные	2. Интервальные
			3. Непрерывные

30. Выборочный метод. Генеральная и выборочная совокупности.

31. Табличное представление экспериментальных данных.

32. Интервалы группировки. Срединные значения интервалов.

33. Понятия частоты, частости, накопленной частоты, накопленной частости. Понятие вариационного ряда.

Вариационным рядом называется ранжированный ряд вариантов с соответ-

ствующими весами (частотами или частостями).

Генеральной совокупностью (популяцией) называется вся совокупность

подлежащих изучению объектов или возможных результатов наблюдений над

одним объектом.

Число, показывающее, сколько раз

встречается вариант x в ряде наблюдений, называется частотой (абсолютной

частотой) варианта nx. 92

Вместо частоты варианта x можно рассматривать ее отношение к общему

числу наблюдений n, которое называется частостью (относительной часто-

той) варианта x и обозначается wx

34. Графическое представление экспериментальных данных (гистограмма, полигон частостей и полигон накопленных частостей).

35. Числовые характеристики выборки.

36. Характеристики положения. Среднее арифметическое, мода и медиана.

37. Характеристики рассеяния. Размах вариации, дисперсия, стандартное отклонение, коэффициент вариации,

Как и среднее линейное отклонение, дисперсия также отражает меру разброса данных вокруг средней величины.

Формула для расчета дисперсии выглядит так:

 

где

D – дисперсия,

x – анализируемый показатель, с черточкой сверху – среднее значение показателя,

n – количество значений в анализируемой совокупности данных

стандартное отклонение. В статистике этот показатель еще называют среднеквадратическим отклонением,

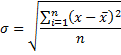
Стандартное отклонение, очевидно, также характеризует меру рассеяния данных, но теперь (в отличие от дисперсии) его можно сравнивать с исходными данными, так как единицы измерения у них одинаковые (это явствует из формулы расчета) среднеквадратическое отклонение дает абсолютную оценку меры разбросанности значений и чтобы понять, насколько она велика относительно самих значений, требуется относительный показатель. Такой показатель существует и называется он коэффициент вариации. Формула коэффициента вариации очень проста: :

 

38. Стандартная ошибка среднего арифметического.

стандартное отклонение распределения средних, которое называется стандартной ошибкой средней или просто стандартной ошибкой. Чем она меньше, тем ближе будет средняя любой конкретной выборки к популяционной средней

39. Характеристики формы. Асиммертия, эксцесс.

Для характеристики степени асимметрии двух или нескольких рядов пользуются коэффициентом асимметрии.

Для одновершинных распределений:

  

Более точным является коэффициент асимметрии, рассчитанный как отношение центрального момента третьего порядка (μ³) к среднеквадратическому отклонению в 3-й степени (Ϭ³):

  

40. Функциональная и статистическая взаимосвязь результатов измерений.

41. Понятие корреляции.

В качестве измерителей степени тесноты парных связей между количественными переменными используются коэффициент корреляции (или то же самое "коэффициент корреляции Пирсона") и корреляционное отношение.

42. Основные задачи корреляционного анализа: выявление направления, формы, степени взаимосвязи случайных величин.

43. Построение диаграммы рассеяния.

Сама диаграмма представляет собой множество (совокупность) точек, координаты которых равны значениям параметров x и y.

Методика построения:

Сведите полученные значения пар данных x, y в таблицу для удобства дальнейшего использования.

Для получения достоверного результата рекомендуется использовать не менее 30 пар данных.

Постройте горизонтальную и вертикальную оси.

Нанесите точки полученных пар значений x, y на график.

1. Вычислите коэффициент корреляции (он позволяет количественно определить силу линейной связи между x и y) по формуле:

Проверьте, что значение полученного коэффициента корреляции не выходит за пределы -1 < r < +1. Если при подсчете получено абсолютное значение r больше 1, значит, в вычислениях произошла ошибка и коэффициент корреляции необходимо пересчитать.

Определите вид связи между x и y, проведя анализ формы построенного графика и вычисленного коэффициента корреляции.

44. Графический анализ корреляционного поля.

45. Коэффициент корреляции. Формула Браве–Пирсона.

Коэффициент корреляции Браве-Пирсона (r) —этопараметрический показатель, для вычисления которого сравнивают средние и стандартные отклонения результатов двух измерений. При этом используют формулу (у разных авторов она может выглядеть по-разному)

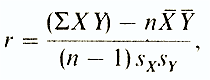
где ΣXY — сумма произведений данных из каждой пары;  n-число пар; X — средняя для данных переменной X; Y— средняя для данных переменной Y S_x — стандартное отклонение для распределения х; S_y — стандартное отклонение для распределения у

46. Достоверность коэффициента корреляции.

Оценка достоверности коэффициента корреляции,полученного методом ранговой корреляции и методом квадратов

Способ 1  Достоверность определяется по формуле:

Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n — 2), где n — число парных вариант. Критерий t должен быть равен или больше табличного, соответствующего вероятности р ≥99%.

Способ 2  Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n — 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95%.

47. Классификация силы взаимосвязи.

48. Коэффициент детерминации.

Для оценки качества модели используют коэффициент детерминации. Долю дисперсии, которая обусловлена регрессией, в общей дисперсии показателя у характеризует коэффициент детерминации R2.

23