
- •Вопросы для подготовки к экзамену по математике для студентов ргуфкСиТ
- •Нахождение обратной матрицы с помощью матрицы из алгебраических дополнений.
- •Алгоритм решения
- •Первый способ задания функции: табличный
- •Второй способ задания функции: с помощью формулы
- •Монотонность функции
- •1) Физический смысл производной.
- •Необходимое условие экстремума
- •3) Третье достаточное условие
Монотонность функции
Функция f(x) называется возрастающей на данном числовом промежутке, если большему значению аргумента соответствует большее значение функции. Функция f(x) называется убывающей на данном числовом промежутке, если большему значению аргумента соответствует меньшее значение функции.
Функция y=f(x) называется четной, если она обладает следующими свойствами: 1) область определения симметрична относительно точки (0; 0), то есть если точка aпринадлежит области определения, то точка -a также принадлежит области определения; 2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)График четной функции симметричен относительно оси Оу
Функция y=f(x) называется нечетной, если она обладает следующими свойствами: 1) область определения симметрична относительно точки (0; 0); 2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T - это период функции
Определение возрастающей функции.
Функция y=f(x) возрастает
на интервале X,
если для любых ![]() и
и ![]() выполняется
неравенство
выполняется
неравенство ![]() .
Другими словами – большему значению
аргумента соответствует большее значение
функции.
.
Другими словами – большему значению
аргумента соответствует большее значение
функции.
Определение убывающей функции.
Функция y=f(x) убывает
на интервале X,
если для любых
и
выполняется
неравенство ![]() .
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
.
Другими словами – большему значению
аргумента соответствует меньшее значение
функции.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Приращение аргумента и приращение функции. Разностное отношение.
Приращением функции f в точке x0 называется разность между значениями функции впроизвольной точке и значением функции в фиксированной точке.
f(х) – f(х0)=f(х0+∆х) – f(х0) – приращение функции f
∆f=f(х0+∆х) – f(х0)

Понятие производной. Понятие дифференциала.
Пусть
функция ![]() определена
в некоторой окрестности точки
определена
в некоторой окрестности точки ![]() и
и ![]() -
произвольная точка из этой окрестности.
Тогда если выражение
-
произвольная точка из этой окрестности.
Тогда если выражение ![]() имеет
предел при
имеет
предел при ![]() ,
то этот предел называется производной функции
в
точке
(обозначается
,
то этот предел называется производной функции
в
точке
(обозначается ![]() ).
).
Функция
,
определенная в некоторой окрестности
точки
,
называется дифференцируемой в
этой точке, если ее приращение ![]() ,
, ![]() представимо
в виде
представимо
в виде ![]() Слагаемое
Слагаемое ![]() называется дифференциалом функции
в
точке
(обозначается
называется дифференциалом функции
в
точке
(обозначается ![]() или
или ![]() )
)
Геометрический и физический смысл производной.
1) Физический смысл производной.
Если
функция y = f(x) и ее аргумент x являются
физическими величинами, то производная![]() – скорость изменения переменной y
относительно переменной x в точке
– скорость изменения переменной y
относительно переменной x в точке![]() .
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная
.
Например, если S = S(t) – расстояние,
проходимое точкой за время t, то ее
производная![]() –
скорость в момент времени
–
скорость в момент времени![]() .
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то
.
Если q = q(t) – количество электричества,
протекающее через поперечное сечение
проводника в момент времени t,
то![]() – скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.
– скорость изменения количества
электричества в момент времени
,
т.е. сила тока в момент времени
.
2) Геометрический смысл производной.
Пусть ![]() –
некоторая кривая,
–
некоторая кривая,![]() –
точка на кривой
.
–
точка на кривой
.
Любая прямая, пересекающая не менее чем в двух точках называется секущей.
Касательной
к кривой
в
точке
называется
предельное положение секущей ![]() ,
если точка
,
если точка ![]() стремится
к
,
двигаясь по кривой.
стремится
к
,
двигаясь по кривой.
Из определения очевидно, что если касательная к кривой в точке существует, то она единственная
Производные основных элементарных функций (формулы), основные правила дифференцирования.
Производные основных элементарных функций.
1)С =
0; 9) ![]()
2)(xm) = mxm-1; 10) ![]()
3) ![]() 11)
11) ![]()
4) 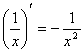 12)
12) ![]()
5) ![]() 13)
13) ![]()
6) ![]() 14)
14) ![]()
7)![]() 15)
15) ![]()
8) ![]() 16)
16) ![]()
Обозначим f(x) = u, g(x) = v- функции, дифференцируемые в точке х.
1) (u v) = u v
2) (uv) = uv + uv
3) ,
если v 0
,
если v 0
Уравнения касательной и нормали к кривой.
Уравнение нормали
Нормаль -- это перпендикуляр к касательной (см. рисунок). Исходя из этого:
tgβ=tg(2π−α)=ctgα=1tgα=1f/(x0)
Т.к. угол наклона нормали -- это угол β1, то имеем:
tgβ1=tg(π−β)=−tgβ=−1f/(x).
Точка (x0,f(x0))∈ нормали, уравнение примет вид:
y−f(x0)=−1f/(x0)(x−x0).
Уравнение касательной
Пусть функция задается уравнением y=f(x), нужно написать уравнение касательной в точке x0. Из определения производной:
y/(x)=limΔx→0ΔxΔy
Δy=f(x+Δx)−f(x).
Уравнение касательной к графику функции: y=kx+b (k,b=const). Из геометрического смысла производной: f/(x0)=tgα=k Т.к. x0 и f(x0)∈ прямой, то уравнение касательной записывается в виде: y−f(x0)=f/(x0)(x−x0) , или
y=f/(x0)·x+f(x0)−f/(x0)·x0.
Вычисление производной сложной функции. Производные высших порядков.
правило дифференцирования сложной функции:
![]()
Сначала находим
производную внешней функции ![]() (синуса),
смотрим на таблицу производных
элементарных функций и замечаем,
что
(синуса),
смотрим на таблицу производных
элементарных функций и замечаем,
что ![]() . Все
табличные формулы применимы и в том,
случае, если «икс» заменить сложным
выражением,
в данном случае:
. Все
табличные формулы применимы и в том,
случае, если «икс» заменить сложным
выражением,
в данном случае:
![]()
Обратите
внимание, что внутренняя функция ![]() не
изменилась, её мы не трогаем.
не
изменилась, её мы не трогаем.
Ну
и совершенно очевидно, что ![]()
Результат применения формулы в чистовом оформлении выглядит так:
![]()
Далее мы берем производную внутренней функции, она очень простая:
![]()
Постоянный
множитель обычно выносят в начало
выражения:
![]()
Готово
Пусть
![]() – некоторая дифференцируемая функция,
производная от которой
– некоторая дифференцируемая функция,
производная от которой ![]() также является дифференцируемой
функцией. Производная функции
также является дифференцируемой
функцией. Производная функции ![]() обозначается символическим выражением
обозначается символическим выражением
![]() и называется второй
производной (или производной
второго порядка)
функции
и называется второй
производной (или производной
второго порядка)
функции ![]() :
:
![]()
Запись вида
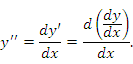
Возрастание и убывание функции. Необходимое и достаточное условие возрастания и убывания функции.
Определение 1. Функция f(x) называется возрастающей в интервале (a,b), если при возрастании аргумента x в этом интервале соответствующие значения функции f(x) также возрастают, т.е. если
f(x2) > f(x1) при x2 > x1
Определение 2. Функция f (x) называется убывающей в интервале ( a, b ) если при возрастании аргумента x в этом интервале соответствующие значения функции f (x) убывают, т.е. если
f(x2) < f(x1) при x2 > x1.
Если дифференцируемая функция y=f(x) возрастает на [a, b], то ее производная неотрицательна на этом отрезке, f '(x)≥ 0.
Обратно. Если функция y=f(x) непрерывна на [a, b], дифференцируема на (a, b) и ее производная положительна на этом отрезке,f ' (x)≥ 0 дляa<x<b, то f(x) возрастает на[a, b].
Если f(x) убывает на[a,b], то
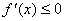 на
этом отрезке. Если
на
этом отрезке. Если 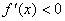 на
(a;
b),
то f(x)убывает
на [a,
b],в
предположении, чтоf(x) непрерывна
на [a,
b].
на
(a;
b),
то f(x)убывает
на [a,
b],в
предположении, чтоf(x) непрерывна
на [a,
b].Доказанная теорема выражает очевидный геометрический факт. Если на [a, b] функция возрастает, то касательная к кривой y=f(x) в каждой точке этого отрезке образует острый угол с осью Ox или горизонтальна, т.е. tga≥0, а значит f '(x)≥0.
Максимум и минимум функции (точки экстремума). Необходимое условие экстремума.
Точки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
Теорема (Необходимое условие экстремума) Если функция нескольких переменных u = f(x1, x2, … , xn) имеет экстремум в некоторой точке, то в этой точке каждая ее частная производная равна нулю или не существует.
Понятие критической точки. Первое достаточное условие экстремума. Наибольшее и наименьшее значения функции на отрезках.
Внутренние точки из области определения функции, в которых выполняются необходимые условия экстремума, называются критическими. Если в критической точке функция дифференцируема, то такая точка называется стационарной.
