Первый способ задания функции: табличный

Если множество   конечно и состоит из   элементов  , то функцию можно задать перечислением, указав, какие значения она принимает на каждом элементе  . Часто это делают в виде таблицы:

В верхней строке таблицы перечисляются все   элементов конечного множества  , а в нижней -- соответствующие им значения функции. Разумеется, таблицу можно расположить и в два столбца вместо двух строк

Второй способ задания функции: с помощью формулы

Если множество   бесконечно, то способ перечисления значений уже не годится. В этом случае функция   может быть задана некоторой формулой, позволяющей по каждому значению аргумента   найти соответствующее ему значение 

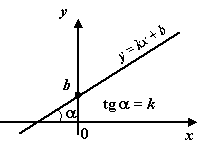
1. Линейная функция. Это функция вида  . Число  называется угловым коэффициентом, а число   -- свободным членом. Графиком   линейной функции служит прямая на координатной плоскости  , не параллельная оси  .

Угловой коэффициент   равен тангенсу угла   наклона графика   к горизонтальному направлению -- положительному направлению оси  . 

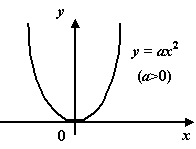
2. Квадратичная функция. Это функция вида   ( ).

Графиком   квадратичной функции служит парабола с осью, параллельной оси  . При   вершина параболы оказывается в точке  . 

3. Степенная функция. Это функция вида  ,  . Рассматриваются такие случаи:

а). Если  , то  . Тогда  ,  ; если число   -- чётное, то и функция   -- чётная (то есть   при всех  ); если число   -- нечётное, то и функция   -- нечётная (то есть   при всех  ). 

б). Если  ,  , то  . Ситуация с чётностью и нечётностью при этом такая же, как и для  : если   -- чётное число, то и   -- чётная функция;если   -нечётное число, то и   нечётная функция.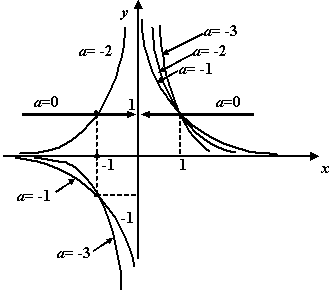

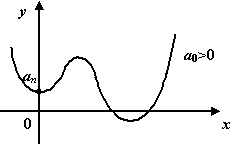
4. Многочлен. Это функция вида  , где  ,  . Число  называется степенью многочлена. При   и   многочлены являются соответственно линейной функцией и квадратичной функцией (квадратным трёхчленом) и рассмотрены выше. При   и   (  ) получается степенная функция, которую мы также рассмотрели выше. В общем случае  ; при чётном значении степени   характерный вид графика таков: 

5. Показательная функция (экспонента). Это функция вида  ( ,  ). Для неё  ,  ,  , и при   график имеет такой вид: 

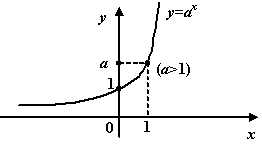
6. Логарифмическая функция. Это функция вида   ( ,  ). Для неё  ,  ,  , и при  график имеет такой вид: 

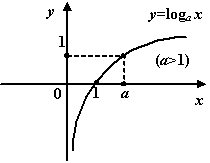
7. Функция синус:  . Для неё  ; функция периодична с периодом   и нечётна. Её график таков: 

8. Функция косинус:  . Эта функция связана с синусом формулой приведения:  ;  ; период функции  равен  ; функция   чётна. Её график таков: 

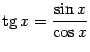9. Функция тангенс:  . По определению,  . Функция  нечётна и периодична с периодом  ;

то есть   не может принимать значений  ,  , при которых   (стоящий в знаменателе) обращается в ноль. 

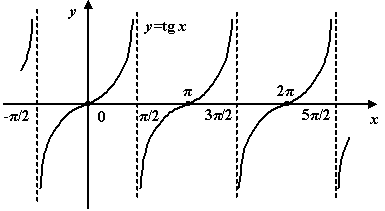
11. Абсолютная величина (модуль):  ,  . Эта функция определяет расстояние на вещественной оси от точки   до точки 0:

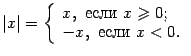
Функция   чётная, её график такой:

12. Обратные тригонометрические функции. Это функции арксинус, арккосинус, арктангенс и арккотангенс. Они определяются как функции, обратные к главным ветвям синуса, косинуса, тангенса и котангенса соответственно.

13. Расстояние до начала координат на плоскости и в пространстве.На координатной плоскости   расстояние   от точки   до точки   определяется по формуле  (по теореме Пифагора) и, следовательно, задаёт функцию

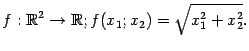
Эта функция имеет область значений

График её ограничения на круг 

Аналогично, расстояние   в пространстве   от точки   до точки   определяется по формуле   и задаёт функцию

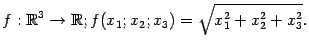
Эта функция имеет ту же область значений

что и в двумерном случае.

14. Арифметическая прогрессия. Функция  , задаваемая формулой

где  ,   -- фиксированные числа, а  , называетсяарифметической прогрессией. Число   называется при этом первым членом прогрессии, а число   -- разностью прогрессии. Функцию   можно представить как ограничение на множество натуральных чисел   линейной функции   с угловым коэффициентом   и свободным членом  . Арифметическую прогрессию можно задать и другим,рекуррентным способом:

 при 

Уравнение, рекуррентно задающее арифметическую прогрессию, -- это линейное уравнение в конечных разностях первого порядка, с одним начальным условием  . 

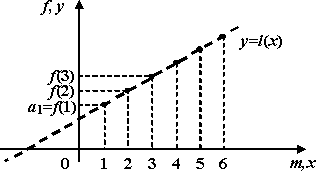
15. Геометрическая прогрессия. Функция  , задаваемая формулой

где  ,   -- фиксированные числа, а  , называетсягеометрической прогрессией. Число   называется при этом первым членом прогрессии, а число   -- знаменателем прогрессии. Функцию   (при  ,  ) можно представить как ограничение на множество натуральных чисел   показательной функции с основанием  , умноженной на постоянный коэффициент  , то есть функции

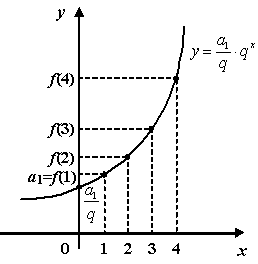
Геометрическую прогрессию можно задать и иначе, рекуррентным способом:

 при 

10. Основные свойства функций (убывание, возрастание и монотонность; четность и нечетность; периодичность).