Вопросы для подготовки к экзамену по математике для студентов ргуфкСиТ

Вопросы для подготовки к экзамену по курсу «Математика» разработаны для студентов, обучающихся по направлениям 032100.62 «Физическая культура», 100200.62 «Туризм», по специальностям: 032101.65 «Физическая культура и спорт», 032103.65 «Рекреация и спортивно-оздоровительный туризм», 100201.65 «Туризм», 032102.65 «Физическая культура для лиц с отклонениями в состоянии здоровья (АФК)», 030602.65 «Связи с общественностью», 050720.65 «Физическая культура».

1. . Матрица. Действия над матрицами.

Определение. Матрицей размера   называется прямоугольная таблица из чисел  , где  , ,

,

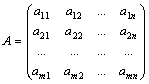состоящая из   строк и   столбцов.

Определение. Суммой   матриц   и   размера   называется матрица   того же размера, каждый элемент которой равен сумме соответствующих элементов матриц А иВ:  , ,  .

Определение. Произведением αА матрицы  на число α называется матрица  , элементы которой  .

Пример 7. Вычислить 3А+2В, если

,  .

Решение. Вычислим  ,  . Тогда  .

Определение. Произведением АВ матрицы   размера   на матрицу   размера   называется матрица   размера  , элемент которой  , стоящий в i-ой строке и j-ом столбце, равен сумме произведений соответствующих элементов i-ой строки матрицы А и j-ого столбца матрицы В:

,

.

Так как строки и столбцы матриц участвуют в произведении АВ неравноправно, то АВ≠ВА.

Пример 8. Вычислить  .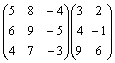

Решение. Умножим элементы первой строки первой матрицы на соответствующие элементы первого столбца второй матрицы и сложим все произведения. Полученный элемент поставим в первую строку и первый столбец матрицы-произведения. Далее вычислим остальные элементы произведения матриц.

.

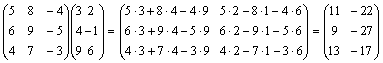Матрицу   называют единичной. Легко проверить, что  , если, конечно, число столбцов матрицы А равно числу строк матрицы Е, и ЕА=А.

Если матрица А имеет одинаковое число строк и столбцов, то ее называют квадратной.

Определение. Определителем квадратной матрицы А называется определитель, составленный из ее элементов.

Обозначают определитель матрицы А либо det A (от слова детерминант, т.е. определитель), либо |A|, либо D.

Определение. Квадратная матрица А называется невырожденной, если ее определитель отличен от нуля. В противном случае матрицу называют вырожденной.

Определение. Матрица   такая, что  , называется обратной матрице А.

Если А – невырожденная матрица, то существует и при этом единственная матрица, обратная к матрице А. При этом  , где  - алгебраические дополнения к элементам исходной матрицы.

Замечание. Следует обратить внимание на то, что алгебраические дополнения к элементам строк матрицы А располагают в столбцах с теми же номерами, что и строки данной матрицы А.

Пример 9. Найти матрицу, обратную к матрице  .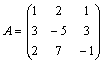

Решение. Вычислим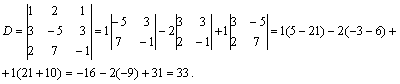 

Найдем алгебраические дополнения соответствующих элементов матрицы А:

,  ,

  ,

,  ,

  ,

,  ,

.

Имеем  .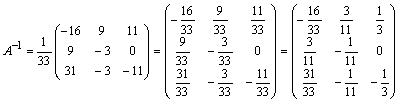

2. Определитель матрицы. Основные свойства определителя.

Квадратной матрице    -го порядка ставиться в соответствие число , называемое определителем матрицы или детерминантом.

Свойства:

1°    При транспонировании квадратной матрицы её определитель не меняется: 

2°    Общий множитель в строке можно выносить за знак определителя.

3°    

То есть, если квадратная матрица    -го порядка умножается на некоторое ненулевое число  , то определитель полученной матрицы равен произведению определителя исходной матрицы   на число   в степени, равной порядку матриц.

4°    Если каждый элемент в какой-то строке определителя равен сумме двух слагаемых, то исходный определитель равен сумме двух определителей, в которых вместо этой строки стоят первые и вторые слагаемые соответственно, а остальные строки совпадают с исходным определителем.

5°    Если две строки определителя поменять местами, то определитель поменяет знак.

6°    Определитель с двумя равными строками равен нулю.

8°    Определитель, содержащий нулевую строку, равен нулю.

9°    Определитель не изменится, если к какой-то его строке прибавить другую строку, умноженную на некоторое число.

10°    Определитель верхней (нижней) треугольной матрицы равен произведению его диагональных элементов.

11°    Определитель произведения матриц равен произведению определителей: 

3. . Методы вычисления определителей.

I. Перестановка двух столбцов (строк) определителя приводит к изменению его знака на противоположный.

II. Умножение всех элементов одного столбца (строки) определителя на одно и то же число, отличное от нуля, приводит к умножению определителя на это число. III. Прибавление к элементам одного столбца (строки) определителя соответствующих элементов другого столбца, умноженных на одно и то же число, не изменяет определитель.

Метод приведения определителя к треугольному виду

При помощи элементарных преобразований любую матрицу можно привести к верхнему (или нижнему) треугольному виду (метод Гаусса). Отсюда следует, что любой определитель, используя перечисленные выше элементарные преобразования, можно привести к треугольному виду, а затем вычислить согласно п.3 замечаний 2.2.

Итак, метод состоит из двух шагов.

1. При помощи элементарных преобразований привести определитель к треугольному виду.

2. Вычислить определитель треугольного вида, перемножая его элементы, стоящие на главной диагонали.

Метод понижения порядка определителя Этот метод также основан на элементарных преобразованиях определителя.

1. При помощи элементарного преобразования III типа нужно в одном столбце (или одной строке) сделать равными нулю все элементы, за исключением одного.

2. Разложить определитель по этому столбцу (строке) и получить определитель меньшего порядка, чем исходный. Если его порядок больше 1, то следует перейти к п. 1, иначе вычисления закончить.

4. Обратная матрица. Нахождение обратной матрицы.