Введение

Счетчиком (Сч) называется цифровой автомат для хранения произвольного n -разрядного числа, позволяющий увеличить (уменьшить) это число на единицу или заданную константу и часто имеющий цепь установки нуля. Счетчики могут выпол­нять также функции приема и выдачи чисел.

Максимальное число устойчивых внутренних состояний счетчика называется его модулем N . Модуль - это максимальное число единичных входных (считаемых) сигналов, которое может сосчитать счетчик. Число триггеров (элементарных автоматов), необходимых для построения счет­чика, равно числу его разрядов и определяется по формуле n = ] log ₂ n [ (скобки ] [ означают округление в сторону большего целого числа).

Входной сигнал вызывает переход счетчика из одного устойчивого состояния в другое. Номера состояний отсчитываются от некоторого начального (нулевого) состояния. Обычно предусматривается возможность перехода счетчика из произвольного состояния в начальное под действием специального управляющего сигнала - установки нуля (УО). Кроме того, счетчик может устанавливаться в начальное состояние после завершения одного цикла работы - подсчета числа входных сигналов, равного модулю счетчика.

По функциональным признакам Сч классифицируется следующим образом.

По модулю счета Сч делятся:

– двоичные счетчики или счетчики по модулю N , где N = 2 ⁿ ;

– т.е. модуль двоичного счетчика равен целой степени числа 2;

– недвоичные счетчики или счетчики по модулю М, где 2 ^n-1<М<2ⁿ

(счетчики с произвольным модулем).

По направлению счета Сч различают: простые (только суммирующие или только вычитающие); реверсивные.

По виду поразрядного переноса различают Сч:

– с параллельным или одновременным переносом (синхронные);

– с последовательным переносом (асинхронные);

– с параллельно-последовательным (комбинированным) переносом.

По порядку изменения состояний Сч делятся: с естественным порядком счета и с произвольным порядком счета.

Простые счетчики могут вести счет только в одном направлении, т.е. только прибавлять входные сигналы к коду, сформированному в счетчике, или же только вычитать входные сигналы из этого кода, реверсивные счетчики ь зависимости от управляющих сигналов могут вести счет как в прямом, так и в обратном направлениях.

Основные характеристики счетчиков, определяющие их быстродей­ствие, - разрешающая способность и время установки (регистрации) кода счетчика. Под разрешающей способностью понимается минимально допустимый период Т следования входных сигналов, при котором счетчик работает без сбоев. Время установки кода представляет собой интервал времени между моментом поступления входного сигнала и момен­том окончания самого длинного переходного процесса в схеме при пере­ходе в новое устойчивое состояние.

Важным частным случаем счетчиков с произвольным модулем являются двоично-десятичные (или просто десятичные) счетчики с модулем счета 2 ³ < M = 10 < 2 ⁴ . Для представления одной десятичной цифры двоично-десятичный счетчик должен содержать не менее четырех триггеров. Но так как четырехразрядным счетчиком можно представить 16 различных состоя­ний, то синтез таких счетчиков заключается в исключении шести избы­точных состояний и обеспечении выбранного порядка пересчета десяти оставшихся состояний.

1. Разработка, синтез и исследование схем счетчиков с произвольным модулем и порядком счета

1.1 Синтез, простых синхронных счетчиков с произвольным порядком счета

Счетчики с произвольным порядком счета отличаются от счетчиков с естественным порядком счета тем, что с приходом очередного входного K сигнала десятичный номер их внутреннего состояния

Изменяется на величину, отличную от единицы. Причины, принуждающие

к использованию таких счетчиков следующие:

– возможность упрощения схемы дешифратора состояний счетчика;

– возможность различения всех возможных состояний счетчика вообще без дешифратора (например, в счетчиках с унитарным кодированием - кольцевых регистрах, в которых циркулирует всего одна единица)

В счетчиках с естественным порядком счета при переходе от одного двоичного числа к соседнему большему или меньшему двоичному числу может происходить изменение цифр одновременно в нескольких разрядах. Это иногда приводит к значительным ошибкам при считывании закодированных угловых и линейных перемещений. Эффективным средством борьбы с ошибками такого рода является использование специальных кодов, называемых отраженными (рефлексными). Отличительная особенность этих кодов заключается в том, что соседние кодовые наборы различаются цифрой только в одном разряде.

В счетчиках с соседним копированием любые ива последовательные состояния будут отличаться только в одном разряде. Последовательные состояния таких счетчиков отображаются на диаграмме Вейча перемещением из любой ее клетки в любую соседнюю (смежную) с ней. В качестве примера соседнего кодирования на диаграмме Вейча (рис. 1.1) показана смена состояний в четырехразрядном счетчике, работающем в широко известном в технике кода Грея, который легко преобразуется в двоичный код. Для данного счетчика можно представить 2⁴ вариантов соседнего кодирования.

Рисунок 1.1 – Пример соседнего кодирования состояний

счетчика (код Грея)

Для удобства восприятия человеком-оператором цифровая измери­тельная информация должна быть представлена в десятичном коде.

В этом случае для передачи обработки и хранения данных обычно исполь­зуются двоично-десятичные коды, которые легко преобразуются в деся­тичный код и просто реализуются техническими средствами. Эти свойства определяют широкое применение двоично-десятичных кодов в информационно-измерительных системах (ИИС) и цифровых устройствах измерения и обработки данных.

В двоично-десятичных кодах каждая десятичная цифра представляется группой цифр, состоящей из четырех двоичных разрядов – двоичной тетрадой. Такая группа позволяет сформировать 15 различных наборов.

В десятичной системе используется только 10 цифр, т.е. шесть наборов избыточны. Так как избыточными могут быть любые шесть наборов, то это приводит к большому числу вариантов построения двоично-десятичных кодов, часть из которых приведена в табл. 1.1.

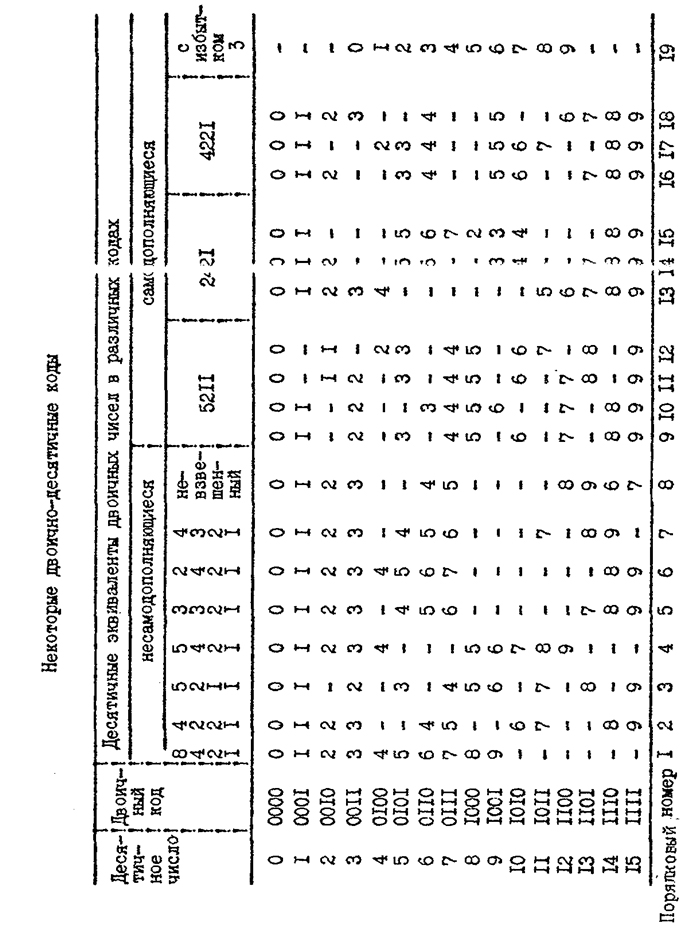
Таблица 1.1– Некоторые двоично-десятичные коды

Пусть каждая десятичная цифра представляется в виде:

где - двоичная цифра, равняя 0 или I; q_i - веса соответствующие разрядов. Видно, что для копирования десятичных цифр от 0 по 9 необходимо, чтобы сумма весов q_i была не меньше 9. Двоично-десятичные коды изображаются перечислением весов всех четырех разрядов, например, код 3421, код 7321 и т.д. (табл. 1.1).

Десятичное число 138₍₁₀₎ в коле 8421 представляется в виде

0001 0011 1000_(2-10) . А в коде 4321в - в виде 0001 0100 1101_(2-10).

Особую группу составляют само-дополняющиеся двоично-десятичные коды. Характерная особенность этих кодов - сумма двоичного кода любой десятичной цифры и ее инверсного двоичного кода (получаемого заменой нуля на единицу и наоборот) должна быть равна двоичному коду цифры 9. Такие колы позволяют легко обнаруживать перенос в старшую тетраду и получать обратный или дополнительный коды при десятичном сложении.

Все перечисленные двоично-десятичные коды называются взвешенными. Каждому разряд в таких кодах поставлен в соответствие определенный вес. Использование взвешенных двоично-десятичных кодов облегчает перевод чисел из одной системы счисления в другую. Однако различают двоично-десятичные коды, называемые невзвешенными, в которых веса разрядов не определены, например, код "с избытком 3".

Синтез любых синхронных двоичных и недвоичных счетчиков с естественным и произвольным порядком счета проводится одинаково с помощью общего метода синтеза цифровых автоматов.

Рассмотрим особенности проектирования синхронных счетчиков с произвольными модулем и порядком счета на примере синтеза двоично-десятичных счетчиков для одного десятичного разряда.

Исходными данными для синтеза является кодированная таблица переходов (КТП) проектируемого счетчика и условная таблица переходов (УТП) выбранного типа элементарного автомата (триггера). Суть синтеза заключается в определении функций возбуждения каждого отдельного триггера и построении по полученным функциям схемы синхронного счетчика.

Для примера спроектируем суммирующий двоично-десятичный счетчик, работающий в невзвешенном коде (см. табл. 1.1). В качестве элементарного автомата выберем универсальный УК-триггер, УТП которого приведена в

табл. 1.2.

Составим кодированную таблицу переходов (см. табл. 1.3) счетчика в выбранном коде, в которой приведены все возможные переходы счетчика из одного состояния в другое.

Считаемый сигнал K в синхронных счетчиках подается на входы синхронизации всех триггеров одновременно. Так как простые счетчики (суммирующие или вычитающие) выполняют только одну микрооперацию, на которую ориентирована их структура, то они не содержат управляющих шин ( l = log₂ 1 = 0 ). Сброс счетчика в ноль будем осуществлять с помощь» асинхронных установочных входов триггеров.

По КТП ССч (см. табл. 1.3) и УТП (см. табл. 1.2) строим кодированную таблицу функций возбуждения (табл. 1.4), из которой извлекаются функции возбуждения триггеров в совершенных формах:

J₄ = V (7) = & (0, 1, 2, 3, 6); J₃ = V (3) = & (0, 1, 2);

K₄ = V (13) = & (14, 15, 12); K₃ = V (13) = & (6, 7, 14, 15, 12);

J₂ = V (1) = & (0, 12, 13); J₁ = V (0, 2, 6, 14, 12) = & (-);

K₂ = V (15) = & (2, 3, 6, 7, 14); K₁ = V (1, 3, 7, 15, 13) = & (-);

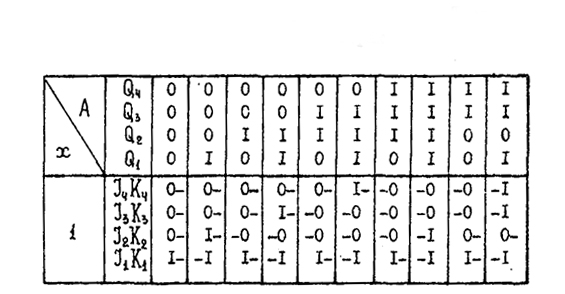
Таблица 1.4 – Кодированная таблица функций возбуждений

синхронного счетчика

Проводим совместную минимизацию фикций возбуждения с помощью диаграмм Вейча:

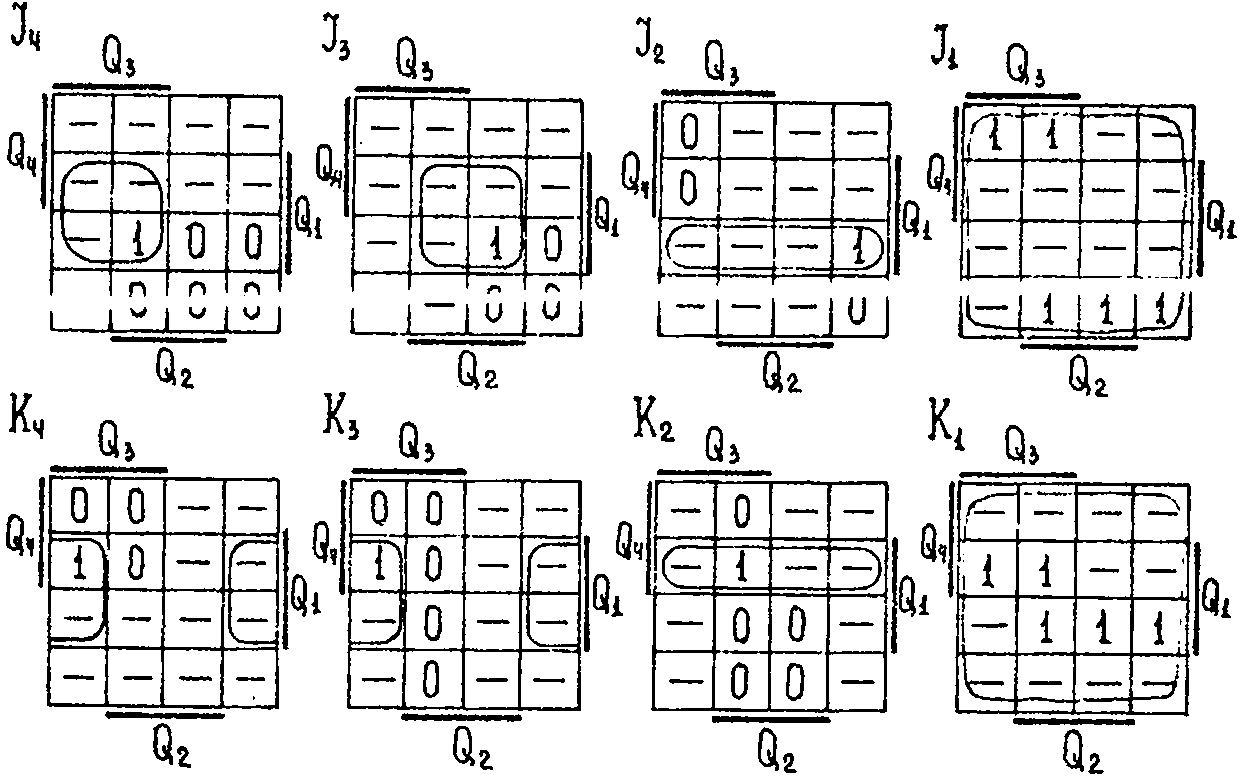
Рисунок 1.5 – Диаграмма Вейча

МДНФ функций возбуждения триггеров проектируемого синхронного счетчика имеют следующий вид:

J₄ = Q₃ Q₁ ; J₃ = Q₂ Q₁ ; J₂ = Q₄ Q₁ ; J₁ = 1 ;

K₄ = Q₂ Q₁ ; K₃ = Q₂ Q₁ ; K₂ = Q₄ Q₁ ; K₁ = 1 ;

Схема спроектированного синхронного счетчика на реальных JK-, триггерах и временная диаграмма его работы показаны на рис. 3.4. Синтез счетчика на основе любого другого типа синхронного триггера

( D, DU, T, RS ) проводится аналогично, разница заключается лишь в использовании соответствующей условной таблицы переходов. Так как реальные триггеры других типов не имеют конъюнктивно связанных инфор­мационных входов, то реализация функций возбуждения таких триггеров проводится с помощью дополнительных логических элементов И-НЕ.

Рисунок 1.6 – Схема суммирующего ССч,

работающего в невзвешенном коде (а)

и временная диаграмма его работы (б).

Перенос между десятичными разрядами двоично-десятичного счет­чика образуется при появлении кода, соответствующего цифре "9''. Если использовать избыточные наборы, то можно минимизировать выражение для сигнала переноса. Для этого необходимо занести на диаграмму Вейча избыточные наборы и набор, соответствующий цифре "9" в данном двоично-десятичном коде, остальные поля диаграммы заполняются нулями. Для рассмотренного выше примера перенос в старший разряд минимизируется диаграммой Вейча и равен P₁= Q₃ Q₁ или P₁ = Q₄ Q_{1 .} Перенос P₁ является синхросигналом для триггеров старшей группы.