23. Дробный факторный эксперимент.

24-25-26??. Критерии оптимальности плана эксперимента

\

Группы критериев:

1. характеризующие точность оценки констант модели ( 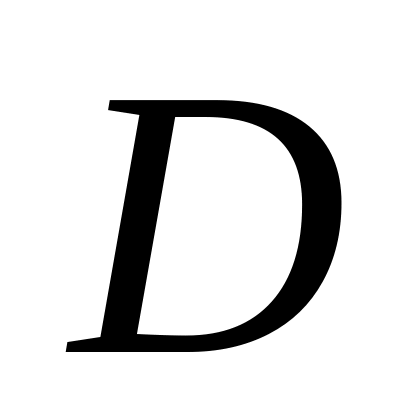, , 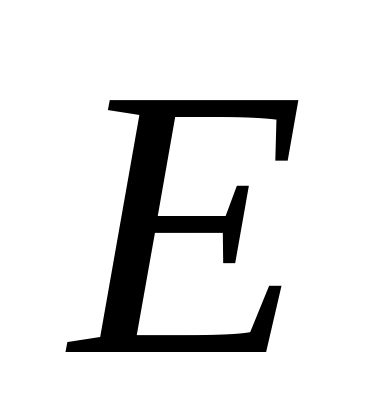) – влияют на матрицу плана;

2. связанные с ошибкой в оценке параметра модели ( 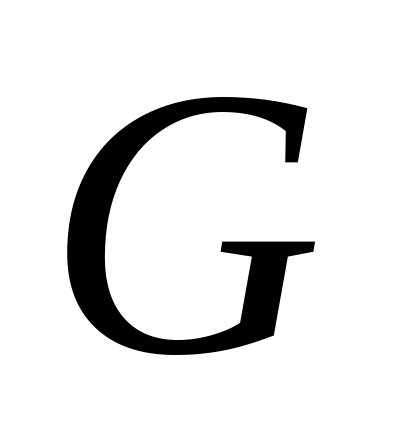, ,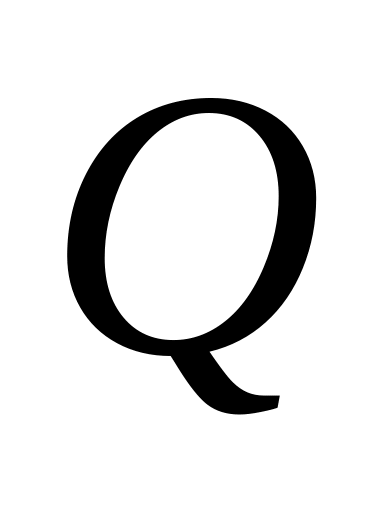 рототабельности, униформности);

3. характеризующие эффективность планирования в целом (насыщенности, экономичности, рабастности, композиционности).

-оптимальности – требует выбор такого плана эксперимента, при котором определитель дисперсионной матрицы имеет минимальную величину (используется в задачах построения нелинейных моделей, в задачах с произвольной областью варьирования параметров и в интерполяционных задачах).

-оптимальности – позволяет выбрать план с дисперсионной матрицей, имеющей минимальный след¹ (применяется, когда требуется обеспечить среднюю точность оценок коэффициентов модели).

-оптимальности – требует выбор такого плана эксперимента, при котором получается наименьшее максимальное собственное значение дисперсионной матрицы (планирование позволяет избежать случая, когда отдельные оценки параметров имеют слишком большую дисперсию и ковариацию).

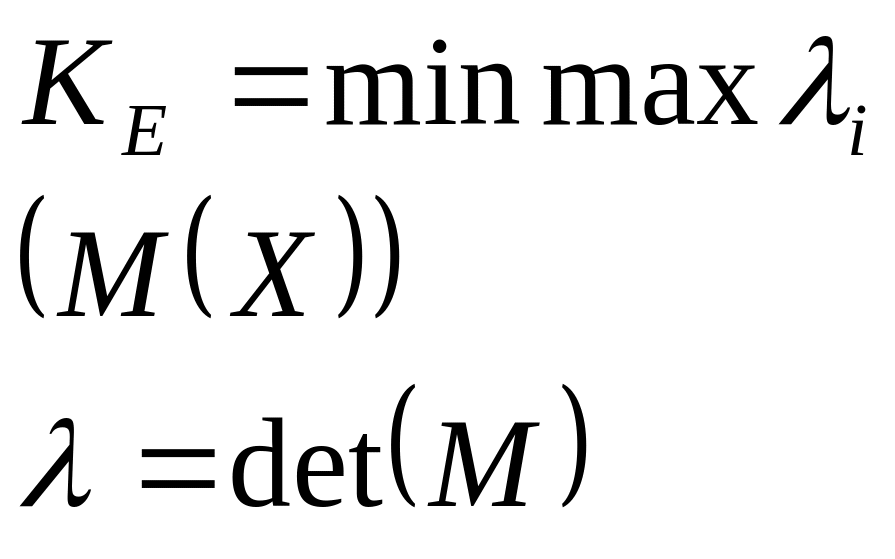
-оптимальности – требует такого расположения точек в области исследования, при котором достигается наименьшая величина максимальной дисперсии оценки независимой переменной (рис1).

-оптимальности

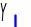
Рототабельности – требует такого расположения экспериментальных точек в области планирования, при котором дисперсия оценки зависимой переменной зависит только от расстояния между точкой и центром плана.(рис.2)

Униформности – требует, чтобы дисперсия оценки модели в некоторой области вокруг центра эксперимента была постоянной.

Насыщенности – одним из основных параметров является объём испытаний . Необходимый объём может быть получен испытаниями элементов (применяется на первом этап исследования, когда важно получить не очень точное представление об объекте при минимуме временных и материальных затрат).

, где - количество констант модели

Экономичности – стремление к минимуму материальных затрат на проведение эксперимента.

Рабастности – означает близость плана к оптимальности одновременно по нескольким критериям.

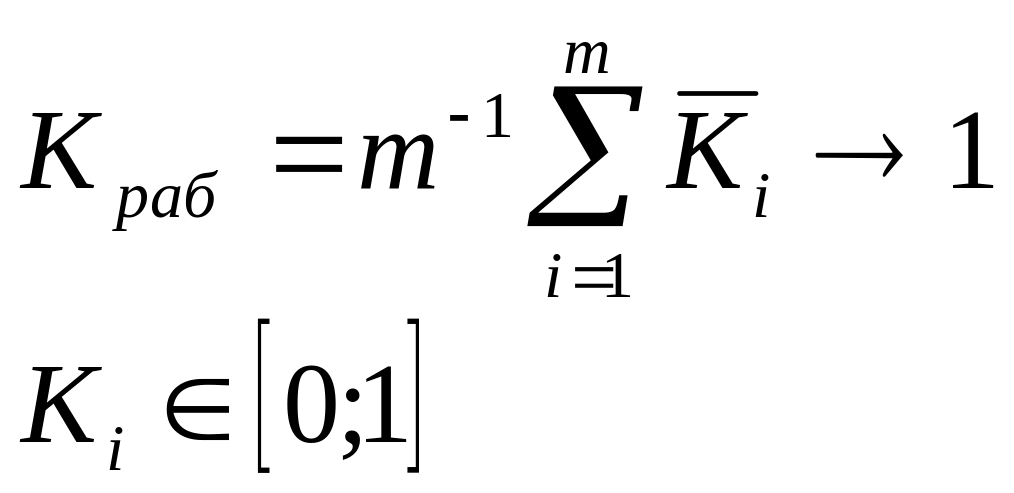
27. Прогнозирование

Математическое прогнозирование заключается в использовании имеющихся данных о характеристиках прогнозируемого объекта соответсвенной обработке этих данных математическими методами получение зависимости связывающих эти характеристики со временем и вычисления характеристик в заданный момент времени.

Этапы:

1 сбор и подготовка данных

2 выбор и обоснование мат. модели

3 обработка данных

4 прогнозирование

Прогнозируемые процессы могут быть:

1-непрерывными

2-дискретными

Виды прогнозов: точечный и интервальный

28. Модели прогнозирования (Хуй знает правильно или нет, в интернете нашел)

модели прогнозирования бывают двух типов: статистические и структурные.

В статистических моделях прогнозирования функциональная зависимость между будущими и фактическими значениями, а также внешними факторами, задана аналитически, т.е. формулой. 

В структурных моделях прогнозирования функциональная зависимость между будущими и фактическими значениями, а также внешними факторами задана структурно, например, в виде графа.