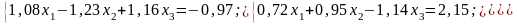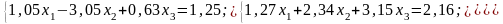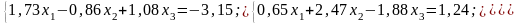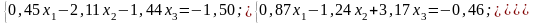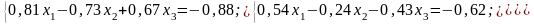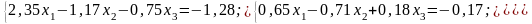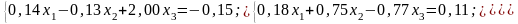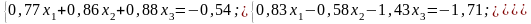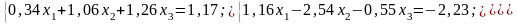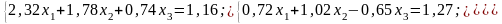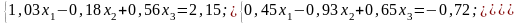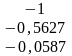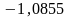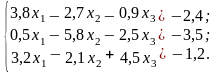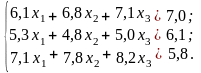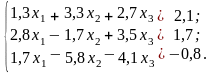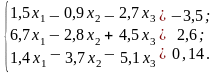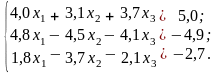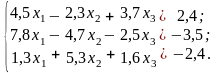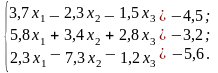Завдання 2.
Розв’язати систему лінійних рівнянь методом головних елементів з точністю до 0,001.
Варіанти до завдання 2
№ 1 |
№ 2 |
|
|
№ 3 |
№ 4 |
|
|
№5 |
№ 6 |
|
|
№ 7 |
№ 8 |
|
|
№ 9 |
№ 10 |
|
|
№ 11 |
№ 12 |
|
|
№ 13 |
№ 14 |
|
|
№ 15 |
№ 16 |
|
|
№ 17 |
№ 18 |
|
|
№ 19 |
№ 20 |
|
|
№ 21 |
№ 22 |
|
|
№ 23 |
№ 24 |
|
|
№ 25 |
№ 26 |
|
|
№ 27 |
№ 28 |
|
|
№ 29 |
№ 30 |
|
|
–––––––––––––––––––––––––––––––––––––––––––––––––––––
Приклад виконання завдання
_____________________________________________________
|
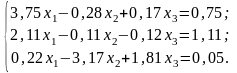
Коефіцієнти при невідомих |
Вільні члени |
|
||
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
;
Контроль:
;
;
.
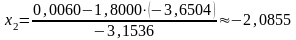Контроль:
;
;
.
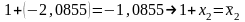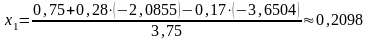Контроль:
.
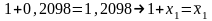Відповідь:
Завдання 3.
Методом Зейделя розв’язати систему лінійних рівнянь з точністю до 0,001, звівши її до виду, зручному для ітерацій.
Варіанти до завдання 3
1.
|
2.
|
3. |
4.
|
5.
|
6.
|
7.
|
8.
|
9.
|
10.
|
11.
|
12.
|
13.
|
14.
|
15.
|
16.
|
17.
|
18.
|
19. |
20.
|
21.
|
22.
|
23.
|
24.
|
25.
|
26.
|
27.
|
28.
|
29.
|
30.
|
–––––––––––––––––––––––––––––––––––––––––––––––––––––
Приклад виконання завдання
_____________________________________________________
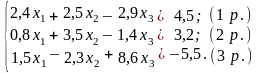
Зведемо систему до вигляду, в якому елементи головної діагоналі перевищували б (за модулем) останні елементи рядків:
Зведемо одержану систему до вигляду зручному для ітерацій:
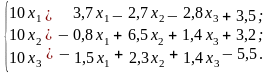
Елементами матриці є числа, які дорівнюють, відповідно, сумі модулів коефіцієнтів при невідомих кожного з рівнянь, тобто
.
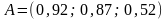Тому
норма
матриці є:
–
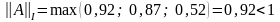процес
Зейделя збіжний.
Обчислення розташуємо в таблиці:
№ |
|
|
|
№ |
|
|
|
0 |
0,3500 |
0,3200 |
-0,5500 |
9 |
0,6029 |
0,5261 |
-0,6057 |
1 |
0,5471 |
0,4230 |
-0,6059 |
10 |
0,6006 |
0,5289 |
-0,6042 |
2 |
0,6079 |
0,4664 |
-0,6196 |
11 |
0,5985 |
0,5311 |
-0,6030 |
3 |
0,6225 |
0,4878 |
-0,6207 |
12 |
0,5969 |
0,5329 |
-0,6020 |
4 |
0,6224 |
0,5004 |
-0,6180 |
13 |
0,5955 |
0,5343 |
-0,6012 |
5 |
0,6182 |
0,5089 |
-0,6148 |
14 |
0,5944 |
0,5355 |
-0,6006 |
6 |
0,6135 |
0,5153 |
-0,6118 |
15 |
0,5935 |
0,5364 |
-0,60008 |
7 |
0,6092 |
0,5202 |
-0,6092 |
16 |
0,5928 |
0,5372 |
-0,5997 |
8 |
0,6055 |
0,5224 |
-0,6070 |
17 |
0,5922 |
0,5378 |
-0,5993 |
Відповідь:
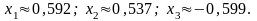
Наведемо ще один, характерний приклад зведення системи до вигляду, зручному для ітерацій.
Нехай маємо систему:
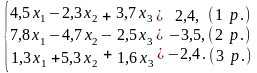
Послідовно одержуємо
,
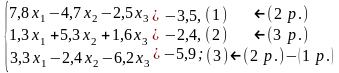
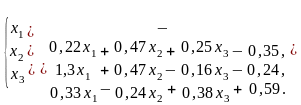
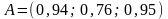