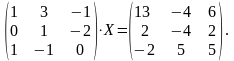- •1. Методи розв’язування систем лінійних рівнянь
- •1.1 Теоретичні відомості
- •1.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
- •Варіанти до завдання 1
- •Завдання 2.
- •Варіанти до завдання 2
- •Приклад виконання завдання
- •Завдання 3.
- •Варіанти до завдання 3
- •Приклад виконання завдання
1.2 Приклади роз’язування завдань та завдання для самостійної і домашньої робіт Завдання 1.
Дослідити систему за допомогою рангів відповідних матриць та розв’язати її: а) за правилом Крамера та методом Гаусса; б) методом Гаусса.
Виконати дії над матрицями.
Розв’язати систему матричним методом.
Розв’язати матричне рівняння.
Варіанти до завдання 1
№1 |
||
1. а)
б) |
2.
3(
|
|
3.
|
4.
|
|
№2 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№3 |
||
1.а)
б) |
2.
=
= |
|
3.
|
4.
|
|
№4 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№5 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№6 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№7 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№8 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№9 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№10 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№11 |
||
1.
а)
б) |
2.
|
|
3.
|
4.
|
|
№12 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№13 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№14 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№15 |
||
1.
а)
б) |
2.
(
|
|
3.
|
4.
|
|
№16 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№17 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№18 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№19 |
||
1.
а)
б) |
2.
|
|
3.
|
4.
|
|
№20 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№21 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№22 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№23 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№24 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№25 |
||
1. а)
б)
|
2.
|
|
3.
|
4.
|
|
№26 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№27 |
||
1. а)
б) |
2.
|
|
3.
|
4.
|
|
№28 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№29 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
№30 |
||
1.а)
б) |
2.
|
|
3.
|
4.
|
|
_____________________________________________________Приклад виконання завдання
а)
 б)
б)
(3A+B)(2A-B), де


_____________________________________________________
а)
 - матриця системи;
- матриця системи;
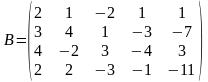 - розширена
матриця системи;
- розширена
матриця системи;
Знайдемо ранги матриць та .


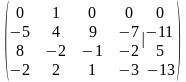
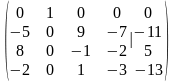





 .
.
Оскільки
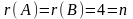 - кількість невідомих, то система а)
сумісна і визначена (має один розв’язок).
- кількість невідомих, то система а)
сумісна і визначена (має один розв’язок).
б)
 - матриця системи;
- матриця системи;
 - розширена матриця системи. Знайдемо
ранги матриць
та
.
- розширена матриця системи. Знайдемо
ранги матриць
та
.




 .
.
Оскільки
 ,
то система б) сумісна і невизначена (має
безліч розв’язків).
,
то система б) сумісна і невизначена (має
безліч розв’язків).
Розв’яжемо системи.
а) правило Крамера:
 =
= =
= =
=
= =
= =
= =
= ;
;


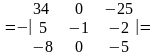
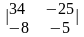 =
= ;
;


 =
= ;
;



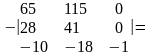
 ;
;




 ;
;

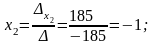


метод Гаусса:
Для того, щоб не мати справи з дробовими числами замінимо перше рівняння системи різницею другого і четвертого (в разі необхідності аналогічно поступатимемо і в інших випадках) та застосуємо метод Гаусса:


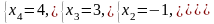
Відповідь:



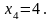
б)


2.
 ;
;
 ;
;


 .
.
3.

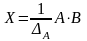 ,
де
,
де
 ,
,
 ,
,
 .
.
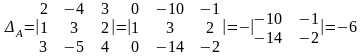 ;
;

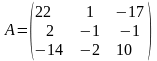 ;
;



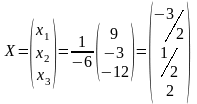 ,
,

4.
Маємо
 ,
звідки
,
звідки
 .
.
 ;
;

 ;
;


 ;
;
 .
.



 )(2
)(2 ),
де
),
де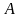 =
=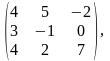
 =
=





 ,
де
,
де
 ,
, .
.



 ,
де
,
де ,
,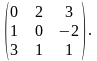
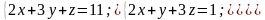



 ,
де
=
,
де
= =
=




 ,
де
,
де





 де
де





 де
де


 .
.

 де
де





 де
де





 де
де





 де
де
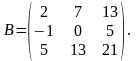




 де
де




 де
де


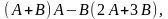 де
де





 )(
)( ),
де
),
де





 де
де





 де
де
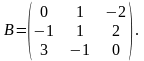




 де
де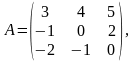





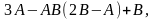 де
де





 де
де





 де
де





 де
де





 де
де




 де
де
 .
.



 де
де





 де
де




 де
де





 де
де




 де
де





 де
де