1. Методи розв’язування систем лінійних рівнянь

1.1 Теоретичні відомості

Норми матриці

:

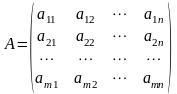- перша норма;

- друга норма;

- третя норма.

Формули Крамера. Нехай дано систему 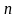рівнянь з невідомими:

Якщо визначник системи відмінний від нуля, то її розв’язок знаходиться за формулами

де

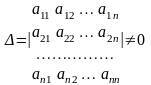- визначник системи,

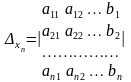
– додаткові визначники для

Схема єдиного ділення (схема Гаусса) для розв’язування системи рівнянь (на прикладі системи чотирьох рівнянь)

Розв’язування проводиться за допомогою таблиці:

Коефіцієнти при невідомих				Вільні члени	Контрольні суми
1
	1
		1
			1
			1
		1
	1
1

Формули для обчислень	Контрольні співвідношення

Метод головних елементів для розв’язування системи лінійних рівнянь

На кожному етапі виключення невідомого вибирають головний елемент – найбільший за модулем коефіцієнт при невідомих, потім знаходять значення 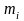, що дорівнюють частці від ділення елементів стовпчика, який містить головний елемент, на головний елемент, що береться з протилежним знаком.

Для одержання елементів наступного етапу додають головний рядок (рядок, що містить головний елемент) до останніх рядків, помноживши його на відповідне значення . Головний рядок в наступному етапі відсутній, оскільки всі його елементи перетворюються в “0”. З нього знаходять невідоме, коефіцієнтом при якому є головний елемент.

Один із можливих варіантів схеми головних елементів наводиться нижче

	Коефіцієнти при невідомих			Вільні члени	Контрольні суми
						1 –й етап
						2-й
	–		–			3-й

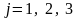В наведеній схемі , де ; ; , де , .

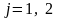Обчислення проводяться за формулами

, ;

; ; ; .

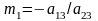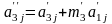
Невідомі знаходять із співвідношень:

;	;
;	;
;	;

Контроль обчислення здійснюють так, як і в схемі єдиного ділення.

Метод послідовних наближень для розв’язування системи рівнянь (метод простої ітерації).

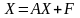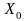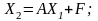
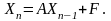Систему необхідно звести до вигляду . Будують послідовність векторів: - довільний вектор; Процес збіжний, якщо для будь-якої норми матриці.

Окремі координати обчислюються за формулами:

,

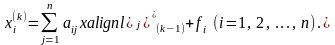
Точність обчислень можна оцінити за співвідношенням

;

якщ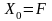о , то

,

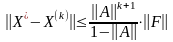де - точний розв’язок.

Метод Зейделя для розв’язування системи рівнянь. Систему необхідно звести до вигляду . Будують послідовність векторів 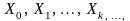де - довільний вектор.

Координати вектора 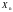визначають за формулою:

.

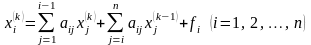Умови збіжності і точність обчислень можна визначити так, як і в методі простої ітерації.
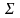
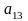
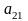
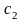
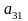
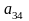
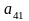
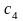
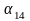
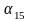
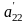
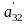
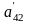
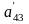
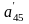
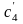
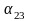
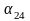
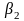
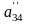
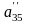
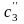
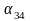
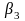
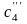
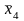
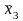
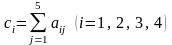
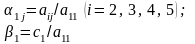
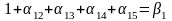
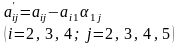
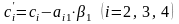
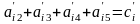
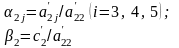
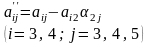
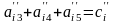
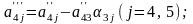
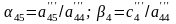
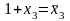
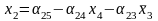
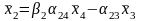
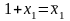
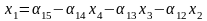
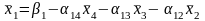
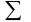
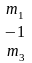
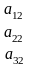
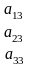
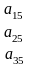
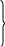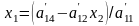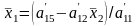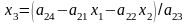