Задание 6
,
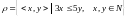
а) Построить примеры пар отношения.
б) Построить графическое представление.
в) Выяснить свойства отношения: Рефлексивность, симметричность, транзитивность, антисимметричность.
Решение:
а) Примеры пар отношения: р = {<1,1>;<1,2>;<1,3>;<1,4>;<1,5>;<1,6>;<1,7>;<1,8>;<1,8>;<1,9>;<1,10>;<2,2>;<2,3>;<2,4>;<2,5>;<2,6>;<2,7>;<2,8>;<2,9>;<2,10>;<3,1>;<3,2>;<3,3>;<3,4>;<3,5>;<3,6>;<3,7>;<3,7>;<3,8>;<3,9>;<3,10>;<4,3>;<4,4>;<4,5>;<4,6>;<4,7>;<4,8>;<4,9>;<4,10>;<5,3>;<5,4>;<5,5>;<5,6>;<5,7>;<5,8>;<5,9>;<5,10>;<6,3>;<6,4>;<6,5>;<6,6>;<6,7>;<6,8>;<6,9>;<6,10>;
б) Графическое представление:
Рефлексивно, т.к. не для любого х есть пара <x;y>, например для х=3 есть пара <3;3>;
Не симметрично, т.к. если 3х ≤ 5у, то 3х ≤ 5у не существует, т.е. для любой пары <x;y> не существует пара <у;х>. Например для пары <1;4> нет пары <4;1>.
Не транзитивно, т.к. если 3х ≤ 5у и 3х ≤ 5z, то это не означает, что 3х ≤ 5z, т.е. не для любых пар <x;y> и <у;z> существует пара <x;z>. Например для пар <10;6> и <6;5> нет пары <10;5>.
Не антисимметрично, т.к. если 3х ≤ 5у, то 3y ≤ 5x не существует, т.е. для любой пары <x;y> не существует пара <у;х>, Например для пары <4;3> есть пара <3;4> при этом 3≠4
Задание
7
«Быть делителем» на множестве натуральных чисел;
Решение:
Рефлексивно, т.к. число делится само на себя, следовательно, для любого ч есть пара <x;х>
Не симметрично, т.к. если х делитель у, то у никак не может быть делителем х, если х≠у. Следовательно, для любой пары для пары <x;y> нет пары <у;х>, таких что х≠у.
Транзитивно, т.к. . если х делитель у, а у делитель z, то х делитель z, следовательно, для любых пар <x;y> и <у;z> есть пара <x;z>;
Антисимметрично, т.к если х делитель у, то у никак не может быть делителем х, если х≠у. . Следовательно, для любой пары для пары <x;y> нет пары <у;х>, таких что х≠у.
«x и y – игроки одного клуба» на множестве футболистов;
Решение:
Рефлексивно, т.к. х играет в том же клубе что х, т.е. для любого х есть пара <x;х>;
Симметрично, т.к. если х и у – игроки одного клуба, то у и х - игроки одного клуба, Следовательно, для любой пары <x;y> есть пара <у;х>;
Транзитивно, т.к. . если если х и у – игроки одного клуба, и у и z - игроки одного клуба, следовательно, для любых пар <x;y> и <у;z> есть пара <x;z>;
Не антисимметрично, т.к. обладает симметрией, т.е. если если х и у – игроки одного клуба, , то у и х - игроки одного клуба. Следовательно, для любой пары <x;y> есть пара <у;х>, такие что х≠у.
2.2 Графы
Задание
1
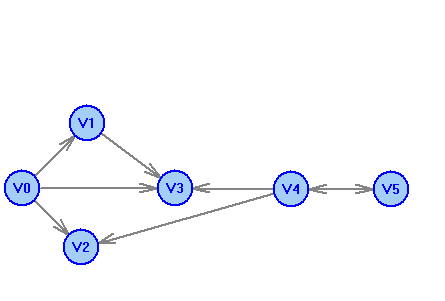
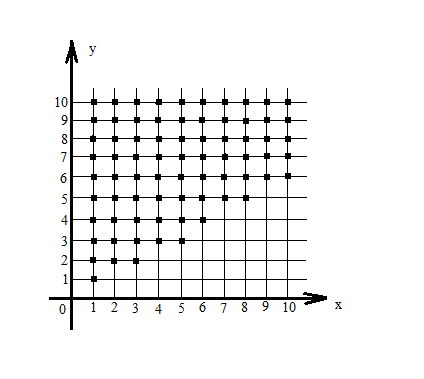
Решение:
Назовем ребра у графа:
Характеристика графа:
Ориентировочный псевдограф D = (V;X)
V = {V0,V1,V2,V3,V4,V5}; X = {X0,X1,X2,X3,X4,X5,X6,X7};
X0 = <V0,V1>, X1 = <V1,V3>, X2 = <V0,V3>, X3 = <V0,V2>
X4 = <V4,V2>, X5 = <V4,V3>, X6 = <V4,V5>, X7 = <V5,V4>.
Специальные вершины и ребра:
Специальных вершин и ребер нет.
Полустепени вершин:
δ-(V0)=3; δ-(V1)=1; δ-(V2)=0; δ-(V3)=0; δ-(V4)=3; δ-(V5)=1;
δ+(V0)=0; δ+(V1)=1; δ+(V2)=2; δ+(V3)=3; δ+(V4)=31; δ+(V5)=1;
Матрицы
смежности, инцидентности, достижимости,
связности.
Матрицы смежности:
|
v0 |
v1 |
v2 |
v3 |
v4 |
v5 |
v0 |
0 |
1 |
1 |
1 |
0 |
0 |
v1 |
0 |
0 |
0 |
1 |
0 |
0 |
v2 |
0 |
0 |
0 |
0 |
0 |
0 |
v3 |
0 |
0 |
0 |
0 |
0 |
0 |
v4 |
0 |
0 |
1 |
1 |
0 |
1 |
v5 |
0 |
0 |
0 |
0 |
1 |
0 |
Матрица инцидентности
-
x0
x1
x2
x3
х4
х5
х6
х7
v0
1
0
1
1
0
0
0
0
v1
-1
1
0
0
0
0
0
0
v2
0
0
0
-1
-1
-1
0
0
v3
0
-1
-1
0
0
1
1
-1
v4
0
0
0
0
1
0
-1
1
v5
0
0
0
0
0
0
0
-1
Матрица достижимости
-
v0
v1
v2
v3
v4
v5
v0
1
1
1
1
0
0
v1
0
1
0
1
0
0
v2
0
0
1
0
0
0
v3
0
0
0
1
0
0
v4
0
0
1
1
1
1
v5
0
0
1
1
1
1
Матрица связности
-
v0
v1
v2
v3
v4
v5
v0
1
0
0
0
0
0
v1
0
1
0
0
0
0
v2
0
0
1
0
0
0
v3
0
0
0
1
0
0
v4
0
0
0
0
1
1
v5
0
0
0
0
1
1
Цикл, цепь, простой цикл, простая цепь:
Простой цикл: V4, X6, V5, X7, V4; Цикл: Нет.
Простая цепь: V0, X0, V1, X1, V3; Цепь: V4, X6, V5, X7, V4;Х5,V3
Задание
2
|
|
|
8 |
|
2 |
|
|
|
4 |
|
6 |
|
7 |
|
4 |
12 |
|
|
|
4 |
8 |
|
|
|
9 |
|
|
|
6 |
|
9 |
|
2 |
1 |
2 |
|
|
|
2 |
|
|
|
7 |
4 |
|
1 |
|
5 |
Решение:
Граф:
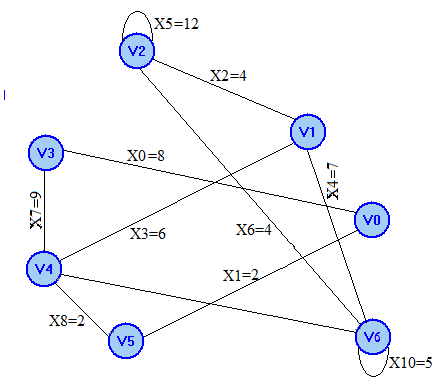
Характеристика графа:
Неориентированный нагруженный граф G=(V,X)
V = {V0,V1,V2,V3,V4,V5,V6}; X = {X0,X1,X2,X3,X4,X5,X6,X7,X8,X9,X10};
X0 = <V0,V3>, X1 = <V0,V5>, X2 = <V1,V2>, X3 = <V1,V4>
X4 = <V1,V6>, X5 = <V2,V2>, X6 = <V2,V6>, X7 = <V3,V4>
X8 = <V4,V5>, X9 = <V4,V6>, X10 = <V6,V6>
Специальные вершины и ребра:
Специальных ребер нет
Х5,Х10 - Петли
Степени вершин:
δ(V0)=2; δ(V1)=3; δ(V2)=2; δ(V3)=3; δ(V4)=2; δ(V5)=2; δ(V6)=5;
Матрицы
смежности, инцидентности, достижимости,
связности.
Матрицы смежности:
-
v0
v1
v2
v3
v4
v5
v6
v0
0
0
0
1
0
1
0
v1
0
0
1
0
1
0
1
v2
0
1
1
0
0
0
1
v3
1
0
0
0
1
0
0
v4
0
1
0
0
0
1
1
v5
1
0
0
0
1
0
0
v6
0
1
1
0
1
0
1
Матрицы инцидентности:
-
x0
x1
x2
x3
х4
х5
х6
х7
x8
x9
x10
v0
1
1
0
0
0
0
0
0
0
0
0
v1
0
0
1
1
1
0
0
0
0
0
0
v2
0
0
1
0
0
2
1
0
0
0
0
v3
1
0
0
0
0
0
0
1
0
0
0
v4
0
0
0
1
0
0
0
1
1
1
0
v5
0
1
0
0
0
0
0
0
1
0
0
v6
0
0
0
0
1
0
1
0
0
1
2
Матрица достижимости:
-
v0
v1
v2
v3
v4
v5
v6
v0
1
1
1
1
1
1
1
v1
1
1
1
1
1
1
1
v2
1
1
1
1
1
1
1
v3
1
1
1
1
1
1
1
v4
1
1
1
1
1
1
1
v5
1
1
1
1
1
1
1
v6
1
1
1
1
1
1
1
Матрица связности
-
v0
v1
v2
v3
v4
v5
v6
v0
1
1
1
1
1
1
1
v1
1
1
1
1
1
1
1
v2
1
1
1
1
1
1
1
v3
1
1
1
1
1
1
1
v4
1
1
1
1
1
1
1
v5
1
1
1
1
1
1
1
v6
1
1
1
1
1
1
1
Цикл,
цепь, простой цикл, простая цепь
Простой цикл: V6, X10, V6
Цикл: V6, X10,V6, X4, V1, X2, V2, X6, V6
Простая цепь: V1, X2, V2, X6, V6
Цепь: V6, X10,V6, X4, V1, X2, V2
Числовые характеристики графа (считаем без нагрузки)
а) Максимальное удаление – r(V) = maxwd(V,W)
r(V0)=4; r(V1)=3; r(V2)=4; r(V3)=4; r(V4)=2; r(V5)=3; r(V6)=4;
б) Диаметр графа d(G) = maxwd(V,W)
d(G) = 4;
в) Радиус графа G-r(G) = minvr(V)
r(G) = 2;
г) Центры графа V ׀ R(G)=r(v)
Центры графа – вершины V4
Остовное дерево и минимальное остовное дерево:
а) Остовным деревом графа называется связной подграф этого графа, содержащий все вершины графа, и не имеющий циклов.
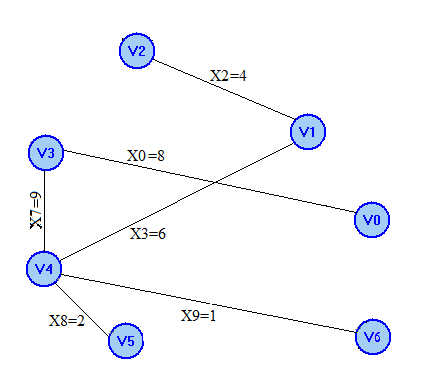
б) Построение МОД:
Алгоритмы:
Дейкстры-Прима
Крускала
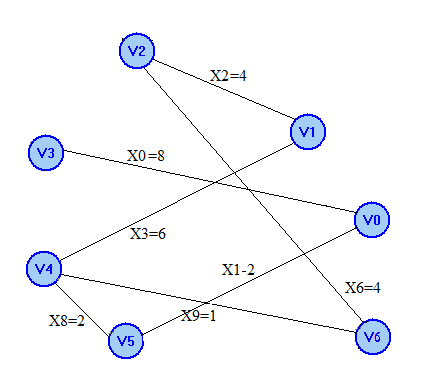
1.V0 1.V4V6
2.V0V5 2. V0V5
3.V5V4 3. V4V5
4.V4V6 4. V1V2
5.V6V2 5. V2V6
6.V2V1 6. V0V3
7.V0V3
Обход граф в глубину и в ширину, начиная с первой вершины:
О
бход
графа в глубину: V0
V1
V2
V3
V2
V6
V2
V1
V5
Обход графа в ширину: 1 ярус: V0
2 ярус: V3,V4
3 ярус: V4
4 ярус: V1
5 ярус: V2,V6
Найти базис циклов графа.
Число циклов в базисе (цикломатическое число графа)
u(G) = m – n + 1 = 11 – 7 + 1 = 5
где m – число ребер в графе;
n – число вершин.
Чтобы найти базис циклов графа, к остовному дереву будем добавлять по одному ребру, которые в остовное дерево не вошли. При этом на каждом шаге будем получать один простой цикл.
1
шаг. Остовное дерево:
2 шаг. Добавим ребро Х1
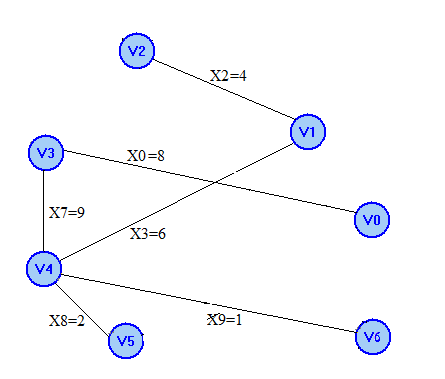
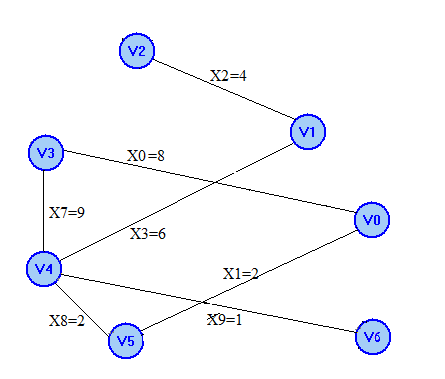
Получим цикл 1: V0 X0 V3 X7 X8 V5 X1 V2
3 шаг. Добавим ребра Х4 4 шаг. Добавим ребро Х5
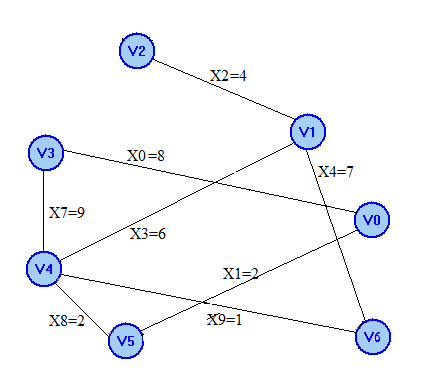
Получим цикл 2: V1 X3 V4 X9 V6 X4 V1 Получим цикл 3: V2 X5 V5
5 шаг. Добавим ребро X6 6 шаг. Добавим ребро Х10
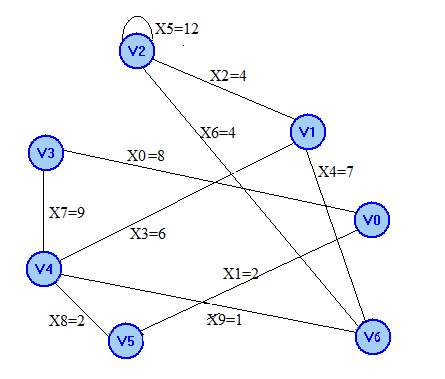
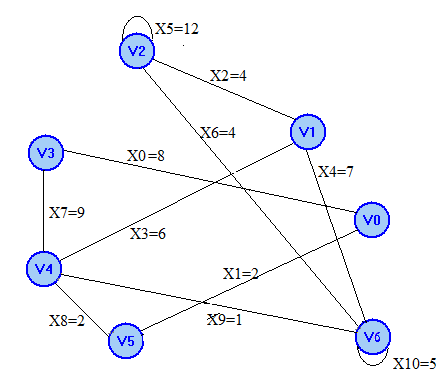
Получим цикл 4: V1 X2 V2 X6 V6 X4 V1 Получим цикл 5: V6 X10 V6
Полученные циклы и образуют базис графа.
