5.3. Формализованное описание сетей Петри.

Для описания и математического анализа процессов с точками ветвления и синхронизации взаимодействия разработан аппарат сетей Петри. Структура сети представляется ориентированным двудольным графом. Множество вершин графа разбивается на два подмножества и , , . Дугами могут связываться вершины из множеств и . Динамика развития процессов отражается в вершинах метками (марками). Распределение меток по вершинам называют маркированием сети. Каждое маркирование соответствует определенному состоянию сети.

Сеть Петри определяется пятеркой , где

, - множество позиций;

, - множество переходов;

- функция следования;

- функция предшествования;

- начальное маркирование (состояние) сети;

- множество положительных целых чисел.

Функции и задают множества дуг и соответственно.

Дуги, предшествующие позиции , обозначим множеством , а дуги, предшествующие переходу , множеством .

Здесь запись означает наличие дуги , а запись - дуги . Аналогично, дуги, следующие из и , представим множествами , .

Входные позиции перехода объединяются в множества его предшественников , а выходные позиции – в множества позиций–последователей .

Маркирование сети представляется вектором , где - число меток в позиции . Переход возбужден при маркировании и может сработать, если выполняется условие , то есть число меток больше или равно числу дуг , что соответствует .

Срабатывание перехода приводит к тому, что каждая позиция теряет меток, а каждая из позиций получает меток.

Если при маркировании возбуждено несколько переходов, то порядок их срабатывания не определен, и, следовательно, может быть представлено несколько последовательностей срабатывающих переходов.

Примеры построения сети Петри

.

Пример 1. В примере рассматривается описание двух взаимодействующих процессов на основе механизма семафоров. Пусть в общей памяти выделен участок длиною единиц, который используется для хранения запросов на выполнение задач. Процессы записи запросов в очередь и выбора их из очереди могут происходить независимо (асинхронно). Описатель очереди содержит четыре элемента: и - число заполненных и свободных ячеек очереди; и - адреса начального и конечного элементов очереди. Алгоритмы записи в очередь и выборки запросов из очереди приведены на рис. 5.9. Запись вида представляет операцию размещения в ячейку очереди с номером , а запись вида - считывание содержимого ячейки и использование его в качестве информации о запросе.

6

4

6

Рис. 5.9. а) – алгоритм постановки запроса в очередь;

б) – алгоритм выборки запроса из очереди;

в) – пример состояния очереди в буфере из ячеек.

С очередью может работать несколько программ «в очередь» и «из очереди». Для организации корректного использования очереди необходимо исключить одновременный доступ программ к области хранения запросов. Иначе возможны ошибки. Например, два потребителя могут выбрать один и тот же запрос, не выбрав из очереди следующий за ним. Для исключения подобной ситуации параллельные процессы «в очередь» и «из очереди» могут синхронизироваться с помощью семафорных примитивов и . Сеть Петри, описывающая эти параллельные процессы, приведена на рис. 5.10. Содержательный смысл позиций и переходов отражен у этих элементов сети.

Рис. 5.10. Сеть Петри, описывающая параллельные процессы управления буферированием: - создание запроса; - запись запроса в очередь; - выполнение запроса; - выборка запроса из очереди.

Позиция - семафор, ограничивающий доступ процесса к очереди. Операции над - переменная увеличивается на 1, если ; - если , то уменьшается на 1, в противном случае процесс блокируется, ожидая состояния семафора . Примитив запрещает доступ процесса в критическую область, а - разрешает.

Аналогично определяются операции над считывающими семафорами и : - если , то уменьшается на 1 и процесс продолжается, иначе он блокируется в текущей точке; - если , то увеличивается на 1 и процесс продолжается.

Пример 2. В данном примере рассматривается ВС (Рис. 5.11), содержащая процессор (П), устройство связи с объектом (УСО) и запоминающее устройство (ЗУ). УСО и П могут работать параллельно.

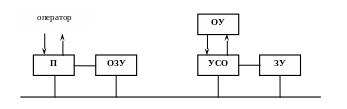
Рис. 5.11. Однопроцессорная ВС с УСО и ЗУ

Процессы в данной ВС порождаются периодическими и инициативными запросами от ОУ и инициативными запросами от оператора. Рассмотрим очередь запросов оператора, которые включают выполнение на П двух операций. Первая из них использует текущие данные из ЗУ. Вторая операция выполняется после первой и завершения работы УСО с ОУ и ЗУ. Сеть Петри, описывающая данный процесс, приведена на рис.5.12.

Рис. 5.12. Модель процесса в виде сети Петри

Переходы: - ввод данных с ЗУ в ОЗУ; - операция 1; - работа УСО с ОУ и ЗУ; - операция 2; - подготовка ЗУ к работе (установка головок).

Позиции: - П свободен; - ввод данных с ЗУ в ОЗУ выполнен; - операция 1 выполнена; - работа УСО закончена; - УСО свободно; - ЗУ готово к работе; - операция 2 выполнена.

Переход срабатывает, если есть запрос, свободный процессор и готовое к работе ЗУ. Возможность параллельной работы процессора и УСО отражена параллельными ветвями с и . Операция 2 (переход ) выполняется по завершению операции 1 и работы УСО. После срабатывания перехода освобождается процессор, ЗУ и фиксируется метка о завершении процесса. После подготовки ЗУ (переход ) может отрабатываться следующий запрос оператора.

В приведенных примерах сети Петри описывали:

• параллелизм и синхронизацию процессов;

• взаимодействие процессов и ресурсов, представленных метками;

• независимые действия, представленные переходами;

• накопители информации (ячейки и буферы) и состояния процессов, представленные позициями.

Однако в рассматриваемом виде сети Петри не позволяют адекватно представлять многие свойства систем. Так, одним из недостатков сетей Петри является отсутствие времени в определении ее динамического функционирования. Большинство теоретических исследований по сетям Петри также исключает из рассмотрения время. При учете времени происходит существенное усложнение в методах анализа сетей и как бы переход от алгебраических уравнений к дифференциальным.

Временные сети. Для учета временных характеристик вводятся временные сети Петри, в которых каждому переходу сопоставляется время . Если переход возбуждается, то метки, вызвавшие запуск перехода, покидают входные позиции . Порождение меток в выходных позициях происходит через время . На множестве переходов с сети Петри может задаваться отношение приоритетности (порядка), определяющее порядок потребления меток возбужденными переходами в условиях конфликта за метку. Временная сеть с приоритетами переходов объединяет возможности, описанные в рассмотренных выше классах сетей.

Раскрашенные сети. Раскрашенные сети Петри являются естественной интерпретацией реальных систем, аналогичной сетям с очередями. Однако сети с очередями не допускают представления эффектов размножения и синхронизации, отражаемых с помощью переходов в сетях Петри. Меткам раскрашенной сети Петри приписывают атрибуты, которые называют цветами. Правила возбуждения переходов дополняются условиями, предполагающими выбор меток определенных цветов из позиций . Срабатывание переходов сопровождается посылкой в позиции меток с задаваемыми значениями цвета.

В ряде случаев на множестве цветов задают отношения приоритетности и сопоставляют их определенным дугам . Правила возбуждения перехода реализуют приоритетный выбор метки для возбуждения перехода на основе значения соответствующего атрибута – приоритета (цвета) метки. Приоритетные раскрашенные сети адекватно представляют приоритетное обслуживание процессов.

Таким образом, процедура раскраски сети Петри – это модельный способ трактовки различных по характеру реальных элементов: в алгоритмах – номера оператора или этапа обработки; в мультипрограммных системах – номера задачи, ее приоритета и других атрибутов; для ресурсов – их типа, способа использования и т.д.

Методы анализа характеристик сетей.

Существуют два базовых метода анализа сетей Петри. Один из них основан на использовании графа достижимых маркировок (диаграммы состояний сети), другой - на применении уравнения состояний и методов линейной алгебры. Статические свойства системы определяет графовая часть сети Петри, а динамические – начальное маркирование и правила возбуждения (моделирования).

Приведем определения некоторых характеристик сетей и их смысловое толкование применительно к задачам анализа систем.

Маркирование называют достижимым из маркирования , если существует последовательность срабатывающих переходов , переводящая сеть из состояния в . Отношение следования маркирований, возбуждаемых действием последовательности имеет вид: .

Переход называют достижимым в сети из маркирования , если существует такое маркирование , достижимое из , при котором происходит срабатывание перехода .

Переход называют живым, если он достижим в из любого , где - множество достижимых маркирований сети.

Сеть - живая, если все ее переходы живые. Доказав, что сеть является живой, можно гарантировать, что в соответствующей системе выполнимы все элементарные действия процессов при их развитии.

Позицию называют -ограниченной, если существует неотрицательное целое , такое что : , где - число меток в позиции .

Сеть - ограниченная, если все ее позиции ограничены, то есть для каждой позиции сети существует предельное число меток, которые могут быть там одновременно. Если метки используются для представления промежуточных данных, созданных системой, то, проанализировав ограниченность сети, можно сделать вывод о возможности потери информации в ВС при ее буферировании.

Сеть - безопасная, если : , то есть при всех достижимых маркированиях ее позиции не могут иметь более одной метки. Анализ безопасности проводится для исключения условий одновременного использования ресурса несколькими процессами. Например, если два сообщения о нем могут одновременно передаваться по каналу или два вычислительных процесса не могут одновременно находиться в критической программной секции, имеет место безопасность маркирования в соответствующих позициях сетевой модели.

Маркировку называют тупиковой, если в этом состоянии сети ни один из переходов не может сработать.

Сеть обладает терминальностью (завершаемостью) процессов, если при всех допустимых начальных маркированиях завершение процессов в ней приводит к тому, что метки покидают сеть, или собираются в некоторой терминальной (конечной) позиции. Терминальность гарантирует работу систем при следующей инициализации без всяких побочных эффектов. Терминальность процессов связана с результативностью алгоритмов (реентерабельностью соответствующих программ). Два перехода, связанные с общей входной позицией являются конфликтными, если они возбуждаются в результате появления метки в . Конфликт за метку из приводит к случайному (недетерминированному) характеру процессов в сети.

Сеть – непротиворечивая, а процессы в ней – детерминированные, если для всех достижимых маркирований множество переходов , возбуждаемых маркированием , равно множеству переходов, срабатывающих при , то есть : .

Проверка свойств сетей может выполняться путем построения и анализа множества достижимых состояний системы. Однако в случае большого количества состояний такой способ затруднителен. Другой способ представляет собой структурный анализ сети на основе заданной матрицы инцидентности и начального маркирования. Динамика сети в пространстве состояний может быть описана рекуррентным уравнением:

; ,

где - состояние, которое следует после состояния в результате -го воздействия ; - начальное маркирование; - матрица, полученная транспонированием матрицы инцидентности позиций и переходов, причем ее элементы равны , , или 0, когда соответственно переход имеет исходящих дуг к позиции , входящих дуг в позицию или не имеет связи с позицией ; – управляющий вектор, компоненты которого . Если , то в -й момент асинхронного времени происходит срабатывание перехода , если же , то срабатывание не происходит.

Для решения рекуррентных уравнений смены состояний сетевых моделей используются методы линейной алгебры. Они позволяют на основе математического исследования структуры биграфа сети и начального маркирования оценить такие качественные характеристики сети как ограниченность, живость и т.д. Для исследования количественных характеристик сетей можно использовать различные методы теории графов и классического сетевого анализа.

Е-сети. В настоящее время теория сетей Петри получила существенное развитие. Так, для описания различных и многообразных свойств систем предлагается язык нагруженных сетей, который легко адаптируется для представления различных частных классов сетевых моделей, и при необходимости объединяет эти частные свойства в едином описании. Расширением языка сетей Петри является язык вычислительных сетей, которые получили название -сети. Так же, как и сеть Петри, -сеть является графом, содержащим вершины двух типов – позиции и переходы и ребра, соединяющие вершины разных типов.

Рис. 5.13. Переходы -сети

В отличие от сети Петри в -сети в множестве позиций выделяют некоторое подмножество, которое соответствует так называемым разрешающим позициям (эти позиции обозначаются буквой ). Каждая позиция -сети может содержать метку. Причем метки могут быть простыми, которые определяют только свободность или занятость данной позиции, или сложными. Сложная метка является вектором, характеризующим множество некоторых параметров. Метки перемещаются по -сети вдоль направленных путей, при этом содержание сложной метки может меняться по мере ее прохождения по сети. Каждая позиция -сети может иметь только одну входящую и одну исходящую дугу. Переходы -сети, как и сети Петри, являются вершинами, в которых происходит преобразование потока меток.

Определено пять типов переходов -сети (элементарных подсетей), из которых составляется сложная -сеть. На рис. 5.13 показаны различные переходы -сети. -, - и -переходы (рис. 5.13, а-в, соответственно) аналогичны переходам безопасной сети Петри. - и -переходы используют разрешающую позицию , которая определяет, на какую выходную позицию -перехода (рис. 5.13, г) перейдет метка с его входной позиции и с какой входной позиции -перехода (рис. 5.13, д) перейдет метка на его выходную позицию.