Магнитное поле. Электромагнитная индукция

§6. Магнитное поле. Индукция магнитного поля.

Магнитный поток

В пространстве, окружающем движущийся электрический заряд и постоянные магниты ( вокруг проводника с электрическим током), создается магнитное поле. Характеристики этого поля зависят от силы тока в проводнике, геометрической формы проводника, расположения данной точки относительно проводника, а также от магнитных свойств среды, в которой находятся проводник и точка. Существенно, что магнитное поле в данной точке создается одновременно всеми участками проводника, по которому течет ток.

Силовой характеристикой магнитного поля является магнитная индукция . Понятие о магнитной индукции вводится на основании одного из трех опытных фактов: а) ориентирующее действие магнитного поля на рамку с током (замкнутый плоский контур с током), б) отклонение проводника с током в магнитном поле; в) отклонение пучка электрически заряженных частиц, движущихся в магнитном поле.

Если в магнитное поле внести рамку с током, то она начнет поворачиваться, при этом на него действует момент сил , модуль которого равен М = p_mB·sin α, [M]=[H^.м] (1)

где В — модуль вектора индукции магнитного поля, а — угол между векторами и (рис. 1), p_m — модуль вектора магнитного момента контура.

Магнитным моментом замкнутого плоского контура, по которому протекает ток силой I (например, рамки с током), называется вектор , равный , [p_m]=[A^.м²]

где S — площадь поверхности, охватываемой контуром, — вектор с модулем, равным единице, направленный перпендикулярно к плоскости контура (единичный вектор нормали). Векторы и перпендикулярны к плоскости контура и ориентированы так, чтобы из их концов ток казался протекающим против часовой стрелки (рис. 2).

Направление единичного вектора нормали и вектора магнитного момента определяется также правилом правого винта (правилом буравчика): если рукоятку буравчика с правой резьбой вращать по направлению тока в контуре (в рамке с током), то направление векторов и совпадает с направлением движения острия буравчика (рис.3).

Магнитное поле называется однородным, если векторы во всех его точках одинаковы. В противном случае поле называется неоднородным.

Из формулы (1) вытекает следующее определение магнитной индукции: модуль вектора магнитной индукции в данной точке однородного магнитного поля равен отношению наибольшего значения момента сил М_макс, действующего на малую рамку с током, помещенную в окрестности данной точки, к модулю магнитного момента p_m:

. [В]=[Тл]

Значение М = М_макс соответствует такой ориентации рамки, при которой α=π/2 радиан, т. е. линии магнитной индукции лежат в плоскости рамки, а ее магнитный момент направлен перпендикулярно к линиям индукции. В этом положении рамка с током будет находиться в неустойчивом равновесии. Устойчивым (равновесным) положение рамки с током или любого замкнутого контура с током будет тогда, когда плоскость рамки перпендикулярна к линии индукции, а вектор магнитного момента рамки направлен вдоль линий магнитной индукции.

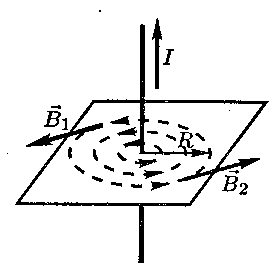
Направление вектора магнитной индукций поля, созданного проводником с током, определяется правилом буравчика (правило правого винта), если движение острия буравчика с правой резьбой совпадает с направлением тока в проводнике, то направление вектора магнитной индукции совпадает с направлением вращения рукоятки буравчика (рис. 4).

Графически магнитное поле изображается при помощи линий магнитной индукции. Линиями магнитной индукции называются воображаемые линии, касательные к которым в каждой точке совпадают с направлением вектора в этих точках поля. Линии магнитной индукции замкнуты. Замкнутость линий магнитной индукции означает, что в природе отсутствуют свободные магнитные заряды. В отличие от электростатического поля, магнитное поле является не потенциальным, а вихревым полем.

Примеры магнитных полей показаны на рис.4 (магнитное поле прямолинейного проводника с током) и рис. 5 (магнитное поле постоянного магнита).

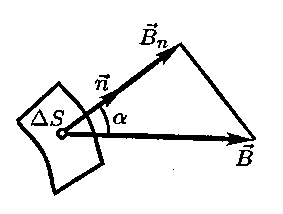
Потоком магнитной индукции (магнитным потоком) ΔФ сквозь участок поверхности с малой площадью ΔS называется скалярная величина, равная ΔФ = BΔS·cos a = B_nΔS, где В_п = В cos а есть проекция вектора магнитной индукции на нормаль к площадке (рис. 6). Положительный (отрицательный) знак магнитного потока соответствует острому (тупому) углу α, или условию В_п > 0 (В_п < 0).

Магнитный поток Ф сквозь поверхность с площадью S находится алгебраическим суммированием потоков ΔФ сквозь участки поверхности. Если магнитное поле однородно, то магнитный поток через плоскую поверхность с площадью S равен Ф = В S cos а. [Ф]=[Вб]

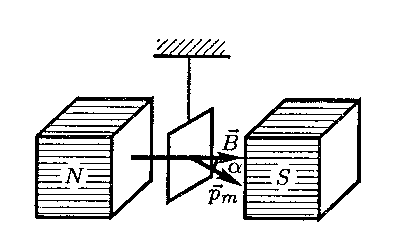
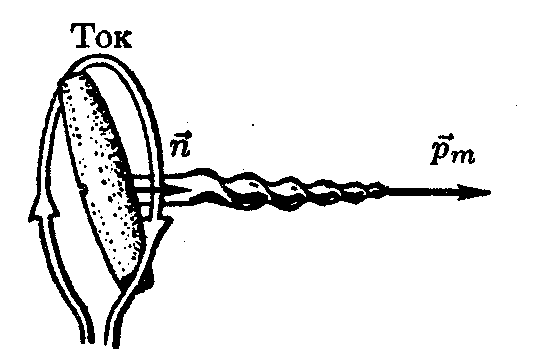
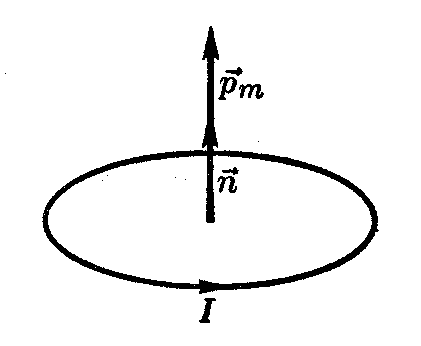
Рис.1 рис.2 рис.3

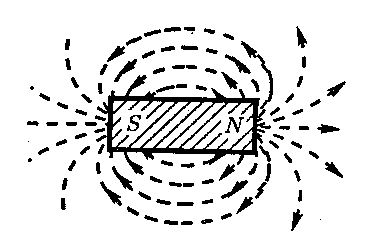
Р ис.4 рис.5 рис.6

Рис. 7 рис.8 рис.9