Метод контурных токов

При расчете методом контурных токов полагают, что в каждом

независимом контуре протекает свой контурный ток. Уравнения

составляют относительно контурных токов, после чего определяют токи

ветвей.

В рассмотренной схеме 3 независимых контура: «1421», «1321»,

«2432» в каждом из которых свой контурный ток I11, I22, I33. В общем

виде система будет выглядеть следующим образом:

где Rmm – полное (собственное) сопротивление независимого

контура m, Rmn – сопротивление между контурами m и n, Ekk –контурная

ЭДС k-го контура. В нашем случае система уравнений и ее решение

будут выглядеть следующим образом:

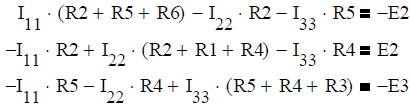
Теперь легко найдем все токи цепи, помня, что токи в смежных ветвях

определяются как результат наложения контурных токов.

Контурные токи I11, I22, I33 здесь представлены с одним индексом I1, I2, I3.

Баланс мощности

Баланс мощности предполагает, что алгебраическая сумма

(т.е.сумма с учетом знака) мощностей источников напряжения, равна

сумме мощностей, рассеиваемой на резисторах (приемниках) Pист =Pпр.

Метод эквивалентного генератора

Этот метод можно применить, когда необходимо найти один ток в

какой-либо ветви схемы. Суть метода заключается в том, что

относительно искомой ветви вся остальная схема представляется

эквивалентным источником ЭДС с внутренним сопротивлением r0. Этот

метод включает следующие операции:

• определяют эквивалентное сопротивление схемы относительно

искомой ветви, т.е. внутреннее сопротивление эквивалентного

генератора;

• определяют напряжение на зажимах генератора на холостом ходу т.е.

его ЭДС.

Итак определим ток I1, методом эквивалентного генератора, на

примере схемы, приведенной выше (рис. 1.1).

Сначала отбросим ветвь, с сопротивлением R1, после чего схема

заметно упростится (рис. 1.2):

Чтобы найти эквивалентное сопротивление относительно зажимов

1-3 надо:

• Закоротить все источники ЭДС;

• оборвать ветви содержащие источники тока (в нашем случае их нет);

• преобразовать один из треугольников в звезду, или наоборот.

Выбираем треугольник, состоящий из сопротивлений R2, R5, R6.

Сопротивления звезды рассчитываются по формулам:

Преобразованная схема приведена на рис. 1.3:

Для этой схемы легко найти эквивалентное сопротивление

относительно зажимов 1-3, оно будет равно:

Теперь найдем напряжение U13 на зажимах генератора.

Для этого в схеме рис.1.4, достаточно рассчитать токи I2 и I3, например

методом двух узлов, относительно 2 – 4.

Зная токи, найдем напряжение U13 на зажимах 1-3

Рассчитав ЭДС генератора и его внутреннее сопротивление, по

закону Ома найдем ток I1:

Как видим, значение тока I1 практически совпадает с ранее

найденным.

Построение потенциальной диаграммы

Выберем контур 4-а-1-3-б-2-4 рис1.1. Примем ψ4=0, тогда:

построим потенциальную диаграмму для контура 4-а-1-3-б-2-4.

1.2 Выполнение ргр 1 в среде ewb

После запуска программы EWB на рабочем поле собирают

заданную схему, в каждую ветвь устанавливают амперметры

постоянного тока, а для построения потенциальной диаграммы

используют вольтметр, один зажим которого постоянно присоединён к

точке, потенциал которой принят за нуль, например к точке 4.(рис 1.5)

рис. 1.5

После нажатия кнопки выключателя в правом верхнем углу

регистрируют показания приборов и делают выводы по работе в целом.

Для измерения ЭДС эквивалентного генератора и его внутреннего

сопротивления поступают следующим образом:

1. удаляют из схемы резистор R1 (рис. 1.6);

2. присоединяют к зажимам 1-3 мультиметр;

3. измеряют напряжение U13;

4. удаляют источники ЭДС E1 и E3;

5. мультиметром измеряют сопротивление r13.

рис. 1.6

2.Расчётно-графическая работа №2

Расчёт и анализ линейной электрической цепи

синусоидального тока

Задание

Для заданной электрической цепи выполнить следующее:

1. Рассчитать комплексы действующих значений токов во всех ветвях

схемы.

2. Определить показания ваттметра.

3. Составить баланс мощности.

4. Построить топографическую диаграмму, совпадающую с векторной

диаграммой токов.

2.1 Выполнение РГР 2 в среде MathCAD

Схема электрической цепи приведена

на рисунке 2.1

её исходные данные:

C1=88.5мкФ; С3=66.25мкФ; L1=100.5мГн; L3=56.9мГн; R2=25 Ом; F=60Гц;

е1=100sin (ωt) В; е3=103.6sin (ωt-30) В.

На рабочем листе программы эти значения следует записать:

Причем значения ЭДС (E1 и Е3) определяются по формуле Эйлера:

Затем рассчитаем реактивные сопротивления катушек и

конденсаторов.

Система уравнений, составленная по первому и второму законам

Кирхгоффа, выглядит следующим образом:

.

Так как уравнения записаны в MathCADe, знаки комплексов

(черта) над символами опущены, а поскольку сопротивления

катушки и емкости определены, как комплексные числа, то в

дальнейшем символ ”i” после них не ставится, а знак “-” перед Xc

учитываем отдельно.

Решение этой системы в MathCADe будет выглядеть следующим

образом:

После того, как токи в цепи определены, можно приступить к

нахождению показаний ваттметра. Ваттметр включен в первую ветвь,

поэтому его показания можно определить по формулам:

где I1- сопряженный комплекс тока I1;

Uab - комплекс напряжения, на которое включен ваттметр.

напряжение Uab найдем по закону Ома, а угол α между током и

напряжением с помощью функции arg( ). Следует помнить, что MathCAD

использует в своих вычислениях радианы, а не градусы. Поэтому при

вычислениях следует использовать формулу перевода углов из

радианной меры в градусную.

На рабочем листе MathCAD расчет мощности будет выглядеть

следующим образом:

После того как подсчитана мощность и найдены все токи,

необходимо составить баланс мощности. Сумма произведений квадратов

модулей токов на сопротивления равна алгебраической сумме

произведений ЭДС на сопряженные комплексы токов.

В результате вычислений мы должны получить два одинаковых

комплексных числа.

После проверки баланса мощности, можно приступить к

нахождению потенциалов различных точек схемы, используя закон Ома

для неоднородного участка цепи. Для этого заземляем любую точку

схемы, например точку а, т.е. считаем, что ее потенциал равен нулю, а

все остальные потенциалы схемы находим относительно заземленной

точки. Например:

После обхода контура потенциал точки “a” вновь должен принять

значение равное “0”. Если это не наблюдается, значит, в расчётах

допущена ошибка.

Можно сказать, что алгебраическая сумма напряжений в

замкнутом контуре равна нулю, и расчеты это подтверждают.

О правильности расчетов можно судить также по взаимному

расположению векторов тока и напряжения на отдельных элементах

схемы. Например, на резисторе R2 вектор напряжения Uab должен

совпадать с вектором тока I2. На участке n-m, где включена

индуктивность, вектор тока I3 отстает (повернут на 90° по часовой

стрелке) от вектора напряжения Unm и так далее.