Д ля нахождения вектора искомых токов записываем
где операция вычисления матрицы, обратной А.
Результат вычисления токов вы ведем на экран:
Теперь выполним тот же самый расчёт методом контурных токов. Примем обход всех независимых контуров по часовой стрелке и обозначим контурные токи I11, I22, I33. Тогда система контурных уравнений примет вид:
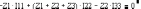
В матричной форме эта система запишется
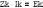
где - матрица сопротивлений системы контурных уравнений ;
- вектор - столбец контурных токов;
- вектор столбец контурных ЭДС.
Запишем и в системе MathCAD.
Тогда исходные контурные токи можно получить:
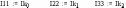
Получим токи ветвей.
Наконец выполним тот же расчёт методом узловых потенциалов. Непосредственно для исходной цепи, изображенной на рис 3.13, метод узловых потенциалов применять нельзя, т.к. проводимость ветви содержащей источник ЭДС, равна бесконечности. Поэтому сделаем эквивалентное преобразование цепи путём переноса источника в смежные ветви ad и ac. После этого узлы а и b объединятся в один узел аb. После такого преобразования цепь примет вид, показанный на рис.3.14.
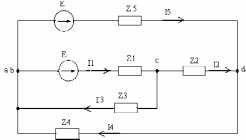
Рис. 3.14. Схема электрической цепи на рис 3.13 после переноса ЭДС.
Преобразованная цепь имеет три узла ab, c, d. Положим потенциал одного из узлов, например ab, равным нулю: , тогда для узлов с, d
система потенциальных уравнений имеет вид:
Или в матричной форме:
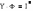
В системе MathCAD запишем выражения для вычисления элементов матрицы Y и I. Напомним, что в матрице Y только диагональные элементы имеют знак плюс, а остальные – знак минус. Диагональные элементы имеют следующий смысл: Ycc есть сумма проводимостей ветвей, сходящихся к узлу «с», Ydd – сумма проводимостей ветвей, сходящихся к узлу «d».
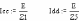
Определим токи в ветвях.
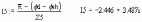
Вывод: Все методы расчёта дали один и тот же результат, следовательно, расчёты верны. Наиболее простым для данной цепи является метод контурных токов.
Пример 3.5. Расчет линейной электрической цепи синусоидального тока методом эквивалентного генератора.
На входе электрической цепи (рис.3.15) действует синусоидальный источник тока J(t). Вычислить мгновенное значение напряжения на сопротивлении нагрузки Rn методом эквивалентного генератора.
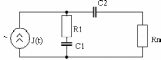
Рис.3.15. Электрическая цепь синусоидального тока
Зададим исходные данные:
в комплексной форме
Представим Rn как нагрузку, а остальную цепь как активный двухполюсник (рис.3.16).
Рис.3.16. Активный двухполюсник
По теореме об эквивалентном генераторе активный линейный двухполюсник можно заменить эквивалентным генератором (рис.3.17), причем Eekv равно напряжению холостого хода, а Zekv равно входному сопротивлению со стороны выводов, к которым подключается нагрузка
Рис.3.17. Эквивалентный генератор
Цепь при холостом ходе имеет вид (рис.3.18):
Рис.3.18.Режим холостого хода
Найдем напряжение холостого хода и входное сопротивление цепи. Ток в С2 отсутствует, так как эта ветвь оборвана. Весь ток источника протекает по ветви, содержащей С1. Свяжем напряжение холостого хода с токами.
.
Отсюда
.
Вычислив параметры эквивалентного генератора, определим ток в нагрузке
и комплексное напряжение на нагрузке
.
Определим мгновенное напряжение на нагрузке
Пример 3.6. Расчет разветвленной линейной электрической цепи синусоидального тока.
Для схемы электрической цепи, изображенной на рис. 3.19, определить комплексы действующих значений токов во всех ветвях, воспользовавшись одним из методов расчёта линейных электрических це-пей, определить показание ваттметра, построить топографическую диаграмму, совмещенную с векторной диаграммой токов. При этом потенциал точки а, указанной по схеме, принять равным нулю. Если
С1= 40 мкФ, L2=199 мГн, R2=25 Ом, С2=10 мкФ, L3=2000 мГн; С3=16 мкФ.
Рис.3.19. Схема разветвленной линейной электрической цепи синусоидального тока
Так как в схеме два узла, наиболее рациональным для расчёта цепи будет метод двух узлов.
Зададим исходные данные:
Комплексные действующие значения ЭДС:
Комплексные сопротивления ветвей:
Напряжение между узлами 1и 2
Токи в ветвях определяем по обобщенному закону Ома
Баланс мощности
Определение показания ваттметра: с помощью выражения для комплексов тока и напряжения на ваттметре и по формуле UIcosφ:
.
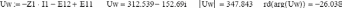
Построение векторной диаграммы тока и напряжения, на которые реагирует ваттметр (рис.3.20):
Рис.3.20. Векторная диаграмма тока и напряжения, на которые реагирует ваттметр
Расчёт топографической диаграммы напряжений:
Потенциал точки а, указанной на схеме (рис. 3.19), принят равным нулю.
Расчет комплексов потенциалов точек цепи
Расчет вещественной и мнимой частей комплексов токов ветвей и потенциалов точек цепи
Построение топографической диаграммы напряжений, совмещенной с векторной диаграммой токов.
Рис. 3.21. Топографическая диаграмма напряжений, совмещенная с векторной диаграммой токов