
- •Министерство образования и науки российской федерации федеральное агентство по образованию
- •Предисловие
- •1.Основные сведения о MathCa
- •1.1.Знакомство с MathCa
- •1.2. Интерфейс пользователя MathCad Рабочее окно
- •Главное меню
- •Состав команд меню File (Файл)
- •Состав команд меню Edit (Правка).
- •Состав команд меню View (Вид)
- •Состав команд меню Insert (Вставка)
- •Hiperlink… [Ctrl-k] (Гиперсвязь):
- •Состав команд меню Format (Форматирование)
- •Состав команд меню Math (Математика)
- •Состав команд меню Symbolic (Символика)
- •Состав команд меню Window (Окно)
- •Состав команд меню Help (Справка)
- •Панели инструментов
- •Стандартная панель (Standard)
- •Панель форматирования (Formatting)
- •1.3. Настройка панелей инструментов
- •2.Основы работы с пакетом MathCad
- •2.1.Простейшие приемы работы
- •2.1.1.Арифметические операции
- •2.1.2.Функции
- •4 Обратные гиперболические функции
- •2.1.3.Работа с комплексными числами
- •Найдём погрешность по напряжениям
- •2.2. Векторы, матрицы и операции с ними
- •2.2.1 Векторы и матрицы
- •2.2.2 Операторы и функции для работы с векторами и матрицами
- •Max(V)- возвращает максимальный элемент
- •Для нахождения вектора искомых токов записываем
- •В матричной форме эта система запишется
- •2.3. Программы-функции
- •2.3.1. Описание программы - функции и локальной оператор присваивания
- •2.3.2. Обращение к программе-функции MathCad
- •2.3.3. Программирование в программе-функции
- •2.3.4. Программирование в программе-функции разветвляющихся алгоритмов
- •2.3.5. Программирование в программе-функции циклических алгоритмов
- •2.3.6. Построение амплитудно-частотной характеристики
- •2.4 Использование в теоретической электротехнике встроенных функций для расчета рядов и определенных интегралов
- •2.4.1 Расчет численным методом определенных интегралов
- •2.4.2 Встроенная функция для расчета рядов
- •2.4.3 Методика расчета установившихся несинусоидальных токов в линейных электрических цепях
- •3.Примеры электротехнических расчетов при использовании вычислений в среде MathCad
- •3.1. Расчет линейной электрической цепи постоянного тока
- •Корни системы уравнений
- •Вводим исходные данные
- •2.Решение задачи c помощью блока решений Given:
- •3.2. Расчет линейной электрической цепи синусоидального тока
- •Найдём погрешность по напряжениям
- •Д ля нахождения вектора искомых токов записываем
- •В матричной форме эта система запишется
- •3.3.Расчет переходных процессов
- •Решим задачу классическим методом. Задание значений параметров элементов цепи:
- •Напряжение на ёмкости c1 было равно e
- •Построение исходного графика зависимости эдс источника от времени (рис.3.28).
- •3.5.Расчет нелинейных резистивных цепей методом полиномиальной аппроксимации Ньютона
- •Из рис.3.36 следует, что уже на 10-й итерации итерационный процесс достигает требуемой точности.
- •Библиографический список
- •Капаев Владимир Иванович Тарасова Наталья Александровна
Вводим исходные данные
 – нумерация
элементов векторов и матриц начинается
с единицы.
– нумерация
элементов векторов и матриц начинается
с единицы.
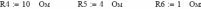
Запишем уравнения по законам Кирхгофа:
I1-I2-I3-I4=0,
I3+I4-I5=0,
I1*(R1+R6)+I2*R2=E1,
I1*R3-I4*R4=-E4,
I4*R4+I5*R5-I2*R2=E4.
В матричной форме это выглядит так:
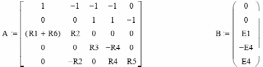
При этом решение выражается в матричном виде
Рассчитаем токи в цепи. При этом решение выражается в матричном виде
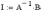
Результат вычисления токов выведем на экран в виде матрицы-столбца токов:
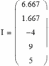
Элементы этой матрицы есть корни системы уравнений, т. е. искомые токи ветвей цепи:
I1=6.667A, I2=1.667A, I3=-4A, I4=9A, I5=5A.
2.Решение задачи c помощью блока решений Given:
Заключается в использовании двух функций системы: Given и Find. Преимущество данного метода заключается в том, что система уравнений вводится в MathCAD без использования матриц, т. е. в "натуральном" виде. Предварительно необходимо только указать начальные значения неизвестных. Это могут быть любые числа, входящие в область определения (часто за них принимают столбец свободных членов). Для решения системы уравнений с помощью блока решений Given MathCAD необходимо задать блок уравнений, который имеет следующую структуру:
1) начало блока (задается с помощью ключевого слова Given);
2) тело блока (сюда входят все уравнения и ограничения);
3) конец блока (заканчивается с помощью выражения Find).
Перед началом блока решений обязательно задаются начальные условия, т.е. начальные значения искомых величин, т.к. решение находится с помощью итераций. При записи уравнений вместо строгого равенства используется знак приближенно равно ≈ . Если поставить строгое равенство, то уравнения разрешены не будут.
Порядок расчета:
Зададим начальные условия:

Начало блока:

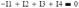
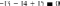
 Тело
блока.
Тело
блока.



Конец блока.
Получаем результат:
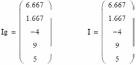
Элементы полученной матрицы есть корни системы уравнений, т. е. искомые токи ветвей цепи:
I1=6.667A, I2=1.667A, I3=-4A, I4=9A, I5=5A.
Как видно из примера расчета токи в цепи, полученные прямым
решением уравнений и полученные с помощью блока решений Given равны.
Выполним проверку баланса мощности:

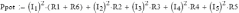
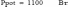
Выполним проверку решения:

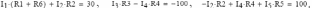
Найденные токи запишем в файл:
 – форма
записи для MathCAD
под Windows.
– форма
записи для MathCAD
под Windows.
3.2. Расчет линейной электрической цепи синусоидального тока
Пример 3.3. Расчет линейной электрической цепи синусоидального тока методом эквивалентных преобразований
Пусть задана электрическая цепь, исходная схема которой изображена на рис. 3.10. Требуется методом эквивалентных преобразований найти токи в ветвях при заданных значениях комплексных сопротивлений и ЭДС:
z1=2+3i; z2=4+5i; z3= ;
z4=10i; z5=-8.1i; E=25.2 .

Рис. 3.10. Исходная схема электрической цепи.
Вначале все комплексные величины, заданные в показательной форме, переведём в алгебраическую форму, в которой MathCAD производит все вычисления (версии MathCAD-2000 и выше эта операция производится автоматически).
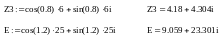
Зададим
все остальные исходные данные
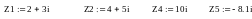
Преобразуем треугольник комплексных сопротивлений z2, z3, z4 в эквивалентную звезду, после чего схема приобретает более простой вид (см. рис. 3.11):
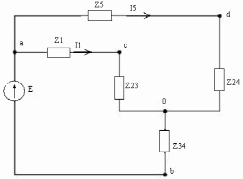
Рис.3.11.Схема электрической цепи после преобразования треугольника в звезду.
Комплексные сопротивления лучей звезды вычисляются по формулам:
z5 и z24 соединены последовательно и эквивалентны сопротивления равно их сумме:
z1 и z23 так же соединены последовательно:
После этих преобразований схема упрощается.

Рис.3.12. Схема после упрощения
Теперь из схемы на рис.3.12 видно, что z123 и z245 соединены параллельно, следовательно, их эквивалентное сопротивление равно

Эквивалентное сопротивление относительно узлов a, b равно сумме сопротивлений z1_5 и z34:
Ток в ветви с источником найдём по закону Ома:
Напряжение между узлами a, o найдём по закону Ома
Напряжение Uob также находится по закону Ома
Токи I1 и I5 схемы рис. 3.12 найдём по закону Ома
Напряжения Udo и Uco также найдём по закону Ома:
Напряжение между узлами c и d найдём как разность напряжений Uco и Udo
Напряжения между узлами c и b , а так же d и b, ищем как суммы
Теперь, когда известны напряжения между всеми узлами электрической цепи на рис. 3.12 найдём все токи исходной цепи
Выполним проверку по законам Кирхгофа.
Найдём погрешность по токам
