3.Примеры электротехнических расчетов при использовании вычислений в среде MathCad
3.1. Расчет линейной электрической цепи постоянного тока
Пример 3.1. Расчет линейной электрической цепи постоянного тока различными методами.
Рассмотрим электрическую цепь постоянного тока, схема замещения которой изображена на рис.3.1. Параметры элементов цепи заданы. Требуется рассчитать токи во всех ветвях цепи различными методами.
Рис.3.1. Исходная схема электрической цепи
Зададим исходные данные для расчета:
1.Рассчитаем токи во всех ветвях с помощью уравнений Кирхгофа.
Выделим в схеме независимые узлы и контуры. Зададим произвольно направления токов в ветвях схемы и направление обхода контуров по ходу часовой стрелки.
Для выделенных независимых узлов и контуров составим систему уравнений по законам Кирхгофа. Предварительно запишем систему уравнений в среде MathCAD не для вычисления, а как комментарий:
по первому закону Кирхгофа:
по второму закону Кирхгофа:
.
Получили
систему линейных алгебраических
уравнений. Решая приведенную систему
уравнений, определяем токи в ветвях
1–8.
При этом учитываем, что ток в ветви 2
известен и равен
.
Решим
полученную систему уравнений матричным
способом. Запишем
полученные уравнения в матричном виде
и из них найдем решение.
Присвоение
переменной
матрицы, состоящей из коэффициентов
при переменных в полученной системе
уравнений
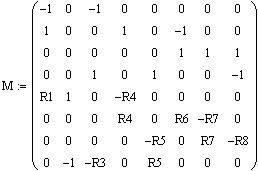
Присвоение
переменной
матрицы, состоящей из столбца свободных
членов полученной системы уравнений
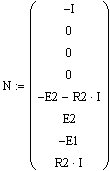
Матричные
уравнения решаются путем обращения
матрицы коэффициентов
.
При этом решение
выражается в матричном виде
,
где
операция вычисления матрицы, обратной
.
Результат
вычисления токов и напряжения
выведем на экран в виде матрицы
Корни системы уравнений:
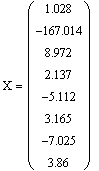
Проверка решения:
возьмем неиспользованный узел 4:
для внешнего контура по второму закону Кирхгофа:
составим баланс мощностей:
Проверка сошлась, следовательно, токи определены верно.
2.Расчитаем токи во всех ветвях схемы методом контурных токов.
Выберем направление контурных токов произвольно (рис.3. 2).
Рис. 3.2. Определение токов во всех ветвях схемы методом контурных токов.
Контурные
токи:
Учтем,
что:
.
В данной схеме 4 независимых контура. Для каждого контура составим контурные уравнения по второму закону Кирхгофа:
,
здесь – контурные токи первого, второго, третьего и четвертого контуров, которые нам нужно найти;
– полные,
или собственные, сопротивления этих же
контуров;
–
контурные
ЭДС соответствующих контуров;
и
т. д. – общие, или взаимные, сопротивления,
входящие одновременно в состав двух
контуров. Знак общего сопротивления
берется "+" если направление
контурных токов на нем совпадают, и "–"
если не совпадают.
Тогда получим:
Определим контурные ЭДС контуров. Если направление ЭДС совпадает с направлением контурного тока, то ЭДС берется со знаком " + ", а если не совпадает то со знаком " – ".
Т.к.
контурный ток
равен току источника тока
т.е.
,
то он известен и не требует определения.
Поэтому матрицу составляем для трех контуров, и решаем ее методом Крамера:
.
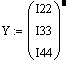
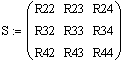При этом решение выражается в матричном виде
.