1. Якщо розподіл числа запитів, які поступили у систему за певний інтервал часу, залежить лише від довжини цього інтервалу і не залежать від розміщення такого інтервалу на осі часу, то такий потік заявок називається
а) рекурентним
б) стаціонарним
в) одинарним
г) потоком без наслідків
д) простим
2. Якщо імовірність поступлення однієї заявки до СМО за нескінченно малий інтервал часу дорівнює нулю, то потік заявок називають
а) простим
б) стаціонарним
в) одинарним
г) потоком без наслідків
д) рекурентним
3. Якщо число заявок, які поступили за інтервали часу, що не перетинаються, є незалежними у сукупності випадковими величинами, то говорять, що такий потік є
а) рекурентним
б) стаціонарним
в) одинарним
г) потоком без наслідків
д) простим
4. Потік заявок, який підпорядкований пуасоновському закону розподілу, називають
а) простим
б) стаціонарним
в) одинарним
г) потоком без наслідків
д) рекурентним
5. На наведене твердження одна або декілька відповідей мають бути вірними
А Б В Г
Якщо вірно тільки Якщо вірно тільки Якщо вірно тільки Якщо вірно тільки
1, 5, 8 2, 7, 8 3, 4, 5 2, 5, 8
При моделюванні стаціонарних потоків заявок найчастіше використовують такі функції розподілу:
Нормальний
Пуасоновський
Стьюдента
Біноміальний
Експоненціальний
Вейбулла
Гама-розподіл
гіперекспоненціальний
6. Рівняння Колмогорова-Чепмена має такий вигляд:
а)
б)
в)
7. Для
системи масового обслуговування з
нескінченим числом станів, інтенсивністю
вхідного потоку
і інтенсивністю обслуговування
визначити ймовірність знаходження в
системі рівно 5 заявок за умови, що
система працює нескінченно довго.
.
а) 0,069; б) 0,067; в) 0,059; г) 0,062
8. Систему масового обслуговування з кінцевим числом станів описують такі зворотні диференціальні рівняння:
а)
б)
в)
9. Задана інфінітезимальна матриця консервативної системи масового обслуговування
.
Чому дорівнює
інтенсивність
?
а) 0,4; б) 0,47; в) 0,87; г) -0,47; д) 0,8
10. Для
системи масового обслуговування з
кінцевим числом станів
,
інтенсивністю вхідного потоку
і інтенсивністю обслуговування
записати інфінітезимальну матрицю
а) б) в)
11. Яке із цих рівнянь, що описує процеси народження і загибелі, буде прямим рівнянням Колмогорова?
а)
12. Яке із цих рівнянь, що описує процеси народження і загибелі, буде зворотнім рівнянням Колмогорова?
в)
13. Ергодичні ймовірності процесів народження і загибелі обчислюються за формулою
,
де величина
це:
а)
б)
в)
14.
Для системи масового обслуговування з
нескінченим числом станів, інтенсивністю
вхідного потоку
і інтенсивністю обслуговування
визначити ймовірність знаходження в
системі рівно
заявок за умови, що система працює
нескінченно довго.
.
а) 0,069; б) 0,067; в) 0,059; г) 0,062
15. Для системи масового обслуговування з нескінченим числом станів, інтенсивністю вхідного потоку і інтенсивністю обслуговування визначити ймовірність знаходження в системі рівно заявок за умови, що система працює нескінченно довго.
.
а) 0,019; б) 0,205; в) 0,015; г) 0,105
16. Для системи масового обслуговування з кінцевим числом станів , інтенсивністю вхідного потоку і інтенсивністю обслуговування записати інфінітезимальну матрицю
а) б) в)
17. Для системи масового обслуговування з кінцевим числом станів , інтенсивністю вхідного потоку і інтенсивністю обслуговування записати інфінітезимальну матрицю
а) ; б)
;
18.
Для системи масового обслуговування з
кінцевим числом станів
,
інтенсивністю вхідного потоку
і інтенсивністю обслуговування
визначити зміну перехідних ймовірностей
в часі.
а)
19. Для системи масового обслуговування з кінцевим числом станів , інтенсивністю вхідного потоку і інтенсивністю обслуговування визначити зміну перехідних ймовірностей в часі.
в)
20.
Система масового обслуговування
називається консервативною, якщо між
інтенсивностями
і
існує таке співвідношення:
а)
;
б)
в)
21. Систему масового обслуговування з кінцевим числом станів описують такі зворотні диференціальні рівняння:
б)
22. Систему масового обслуговування з кінцевим числом станів описують такі прямі диференціальні рівняння:
а)
23. Яке із цих рівнянь є математичною моделлю консервативних систем масового обслуговування?
в)
24. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
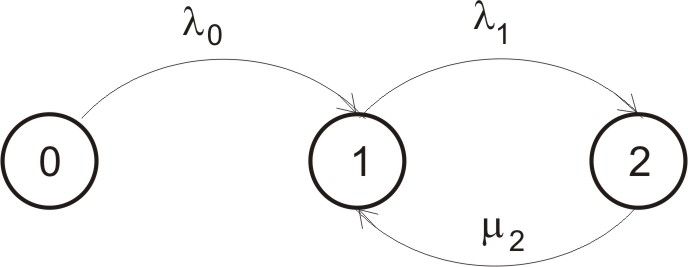
укажіть, який із
наведених розв’язків описує її
функціонування, якщо
,
і
;
=0,8,
=0,85.
а)
,
,
,
25. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
укажіть, який із наведених розв’язків описує її функціонування, якщо , і ; =1,8, =1,85.
в)
,
,
26. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
визначити ймовірність
знаходження системи в стані
при нескінченно довгій її роботі, якщо
,
і
;
=0,1,
=0,15.
а) 0,4852; б) 0,5244; в) 0,2105; г) 0,4138; д) 0,3103
27. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
визначити ймовірність
знаходження системи в стані
при нескінченно довгій її роботі, якщо
,
і
;
=0,1,
=0,15.
а) 0,4138; б) 0,5244; в) 0,2105; г) 0,4852; д) 0,4737
28. Для консервативної системи масового обслуговування, граф якої показаний на рисунку,
визначити ймовірність
знаходження системи в стані
при
нескінченно довгій її роботі, якщо
,
і
;
=0,1,
=0,15.
а) 0,4138; б) 0,5244; в) 0,2759; г) 0,4852; д) 0,4737
29. Задана інфінітезимальна матриця консервативної системи масового обслуговування
.
Чому дорівнює
інтенсивність
?
а) 0,4; б) 0,47; в) 0,87; г) -0,47; д) 0,8
30. Задана інфінітезимальна матриця консервативної системи масового обслуговування
.
Чому дорівнює інтенсивність ?
а) 0,4; б) 0,47; в) 0,87; г) -0,47; д) 0,8
31. Задана інфінітезимальна матриця консервативної системи масового обслуговування
.
Чому дорівнює
інтенсивність
?
а) 0,4; б) 0,47; в) 0,87; г) -0,47; д) 0,8
32. Інтенсивності переходів марківського процесу обчислюються за такою формулою:
а)
;
б); в).
33.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 0,18; б) 0,36; в) 0,72; г) 0,54
34.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 0,18; б) 0,72; в) 0,36; г) 0,54
35.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 0,18; б) 0,36; в) 0,54; г) 0,72
36.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 1,08; б) 0,36; в) 0,72; г) 0,54
37.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 1,08; б) 0,36; в) 0,72; г) 1,00
38.
Система складається із N
приладів, час безвідмовної роботи,
кожного із них експоненціально-розподілена
випадкова величина з параметром .
Число елементів, що знаходяться в момент
часу
в неробочому стані Хt=0,1,...,n.
Є r
n
операторів, кожен із яких може одночасно
відновлювати лише один прилад. Якщо
число приладів, що відмовили більше r,
то r
елементів
відновлюються, інші утворюють чергу на
відновлення. Тоді інтенсивність переходу
системи із стану
в
стан
при
,
,
буде дорівнювати:
а) 1,08; б) 3,5; в) 2,5; г) 1,00
39. На рисунку показаний граф системи масового обслуговування.
До якого типу систем МО можна віднести таку систему?
д) система з втратами
40. На рисунку показаний граф системи масового обслуговування.
До якого типу систем МО можна віднести таку систему?
б) багатолінійна система із обмеженим часом очікування;
41. На рисунку показаний граф системи масового обслуговування.
До якого типу систем МО можна віднести таку систему?
в) багатолінійна система із загальним накопичувачем;
42. На рисунку показаний граф системи масового обслуговування.
До якого типу систем МО можна віднести таку систему?
в) багатолінійна система із загальним накопичувачем;
г) система з очікуванням;
д) система з втратами
43. На рисунку показаний граф системи масового обслуговування.
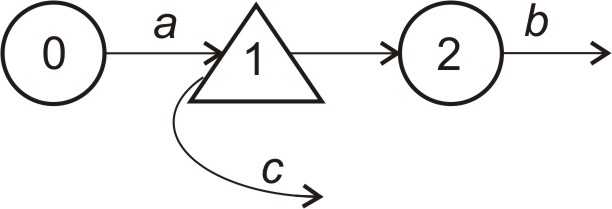
До якого типу систем МО можна віднести таку систему?
в) система з обмеженим накопичувачем;
44. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – пуасоновський, послідовність вимог – незалежна з рівномірним законом розподілу
д)
45. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – рекурентний, послідовність вимог – незалежна з рівномірним законом розподілу
б)
г)
46. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – рекурентний, послідовність вимог – незалежна з експоненціальним законом розподілу
а)
47. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – пуасоновський, послідовність вимог – незалежна з експоненціальним законом розподілу
г)
48. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – рекурентний з розподілом Ерланга, послідовність вимог – незалежна з експоненціальним законом розподілу
в)
49. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік вимог – рекурентний з розподілом Ерланга, послідовність вимог – незалежна з рівномірним законом розподілу
б)
50. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік – з постійними інтервалами між вимогами, послідовність вимог – незалежна з рівномірним законом розподілу
д)
51. Запишіть символіку системи масового обслуговування, якщо кількість обслуговуючих приладів – 7, ємність накопичувача – 40, потік – з постійними інтервалами між вимогами, послідовність вимог – незалежна з експоненціальним законом розподілу
а)
52.
В системі масового обслуговування типу
М/М/1/0 ергодична ймовірність того, що
прилад не занятий операцією обслуговування
буде такою (
,
):
а) 0,455; б) 0,625; в) 0,725; г) 0,545; д) 0,375
53. В системі масового обслуговування типу М/М/1/0 ергодична ймовірність того, що прилад занятий операцією обслуговування буде такою ( , ):
а) 0,625; б) 0,455; в) 0,725; г) 0,545; д) 0,375
54. В системі масового обслуговування типу М/М/1/0 ймовірність того, що прилад не занятий операцією обслуговування буде такою ( , ):
д)
55. В системі масового обслуговування типу М/М/1/0 ймовірність того, що прилад занятий операцією обслуговування буде такою ( , ):
а)
в)
56.
В системі масового обслуговування типу
М/М/5/8 ергодична ймовірність того, що в
черзі буде знаходитись рівно 4 вимоги
є такою (
,
,
):
а) 0,025; б) 0,061; в) 0,047; г) 0,027; д) 0,055
57. В системі масового обслуговування типу М/М/5/8 ергодична ймовірність того, що в черзі буде знаходитись рівно 2 вимоги є такою ( , , ):
а) 0,262; б) 0,35; в) 0,47; г) 0,33; д) 0,55
58. В системі масового обслуговування типу М/М/5/8 ергодична ймовірність того, що в черзі не буде жодної вимоги є такою ( , , ):
а) 0,262; б) 0,35; в) 0,47; г) 0,189; д) 0,55
59.
В системі масового обслуговування типу
М/М/5/8 ергодична ймовірність того, що в
черзі буде знаходитись рівно 6 вимог є
такою (
,
,
):
а) 0,262; б) 0,35; в) 0,161; г) 0,189; д) 0,55
60. В системі масового обслуговування типу М/М/8/ ергодична ймовірність того, що в черзі буде знаходитись рівно 2 вимоги є такою ( , ):
а) 0,262; б) 0,35; в) 0,244; г) 0,189; д) 0,145
61.
В системі масового обслуговування типу
М/М/8/ ергодична ймовірність того, що в
черзі буде знаходитись рівно 1 вимога
є такою (
,
):
а) 0,262; б) 0,359; в) 0,144; г) 0,189; д) 0,145
62.
В системі масового обслуговування типу
М/М/5/ ергодична ймовірність того, що в
черзі буде знаходитись рівно 4 вимоги
є такою (
,
):
а) 0,130; б) 0,35; в) 0,144; г) 0,189; д) 0,145
63. В системі масового обслуговування типу М/М/5/ ергодична ймовірність того, що в черзі буде знаходитись рівно 6 вимог є такою ( , ):
а) 0,0130; б) 0,039; в) 0,0144; г) 0,0189; д) 0,033
64. В системі масового обслуговування типу М/М/5/4 ергодична ймовірність того, що в черзі буде знаходитись рівно 3 вимоги є такою ( , , ):
а) 0,0130; б) 0,039; в) 0,052; г) 0,0189; д) 0,033
65. В системі масового обслуговування типу М/М/5/4 ергодична ймовірність того, що в черзі буде знаходитись рівно 6 вимог є такою ( , , ):
а) 0,130; б) 0,106; в) 0,144; г) 0,189; д) 0,145
66. В системі масового обслуговування типу М/М/5/4 ергодична ймовірність того, що в черзі буде знаходитись рівно 7 вимог є такою ( , , ):
а) 0,130; б) 0,106; в) 0,144; г) 0,159; д) 0,145
67. В системі масового обслуговування типу М/М/5/4 ергодична ймовірність того, що в черзі буде знаходитись рівно 8 вимог є такою ( , , ):
а) 0,130; б) 0,106; в) 0,144; г) 0,159; д) 0,124
68.
Багатолінійна система масового
обслуговування типу M/M/N/
характеризується трьома параметрами
,
і
.
При яких значеннях параметрів
,
і
ергодичні ймовірності існують?
а) , і - додатні величини
69.
Багатолінійна система масового
обслуговування типу M/M/N/
характеризується трьома параметрами
,
і
.
При яких значеннях параметрів
,
і
ергодичні
ймовірності існують?
в)
70.
Мережа
називається зв’язаною, якщо при
будь-якому розбитті множини вузлів на
дві підмножини
і
знайдеться дуга
або
така, що
а)
і
71.
Послідовність дуг і вузлів мережі
,
,
,
,
,
…,
,
,
,
яка починається у вузлі
і закінчується вузлом
називається
в) ланцюгом
72. Потоком
у мережі із джерела
до стоку
називається множина невід’ємних чисел
(кожне із яких поставлено у відповідність
деякій дузі мережі) за умови, що ці числа
задовольняють наступним лінійним
обмеженням:
а)
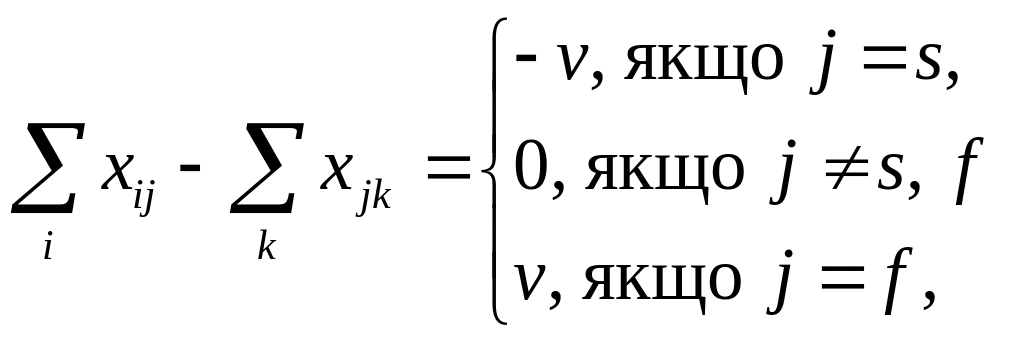
73.
Пропускною
здатністю
(величиною) січення
називається
величина
в)
,
74. Перетином називають
а) мінімальне число дуг
75. У будь-якій мережі величина максимального потоку із джерела до стоку дорівнює пропускній можливості
б) мінімального перерізу
який розділює і .
76. Для
мережі, яка зображена на рисунку, знайти
пропускну здатність січення, якщо
.
в) 9;
77. Для
мережі, яка зображена на рисунку, знайти
пропускну здатність січення, якщо
.
а) 10;
78. Для
мережі, яка зображена на рисунку, знайти
пропускну здатність січення, якщо
.
а) 10
79. Доповнити потік у мережі, яка зображена на рисунку, так щоб мало місце збереження потоку
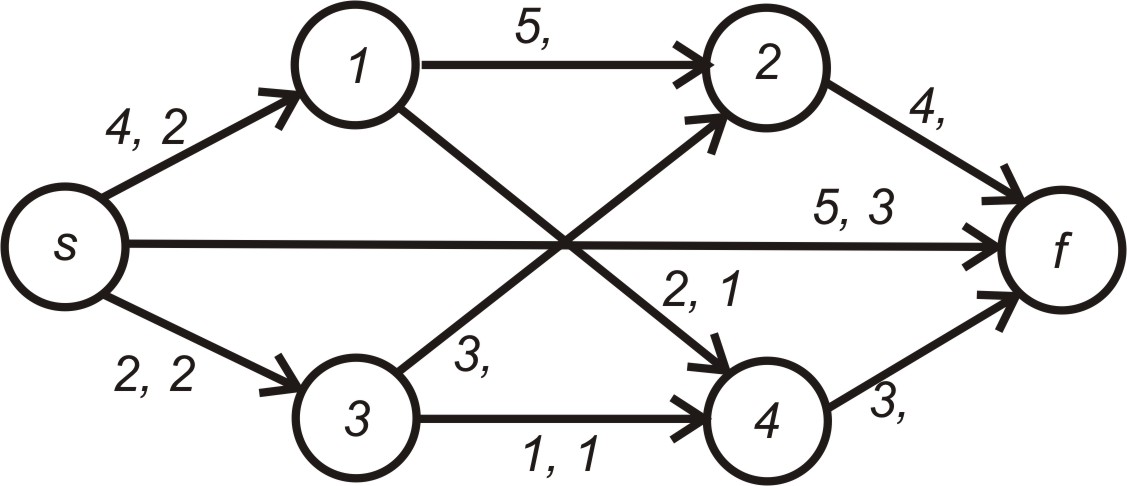
г)
- 5, 1;
- 4, 2;
- 3, 1;
- 3, 2
80. Для якого вузла не виконується збереження потоку у мережі, яка показана на рисунку
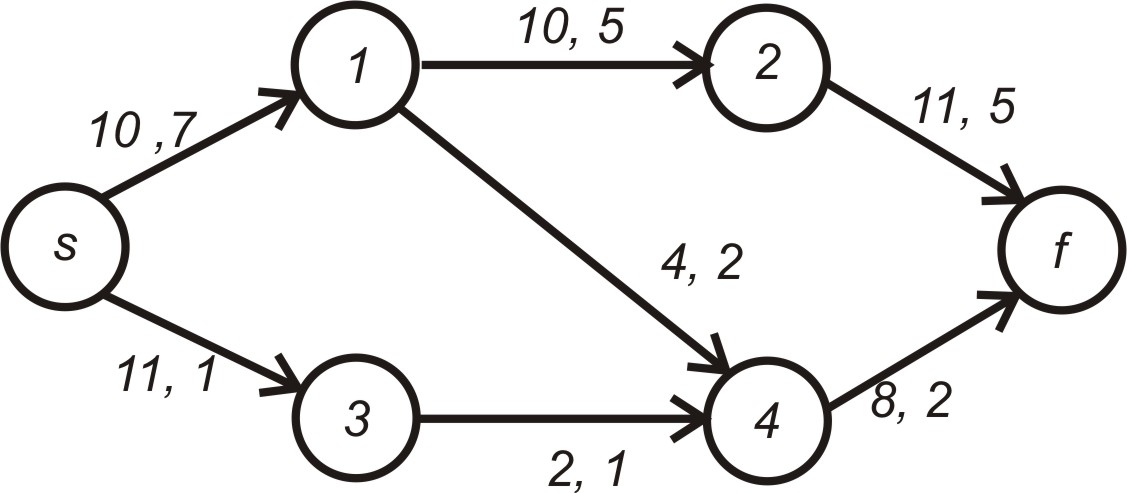
д)
81. Доповнити потік у мережі, яка зображена на рисунку, так, щоб мало місце збереження потоку
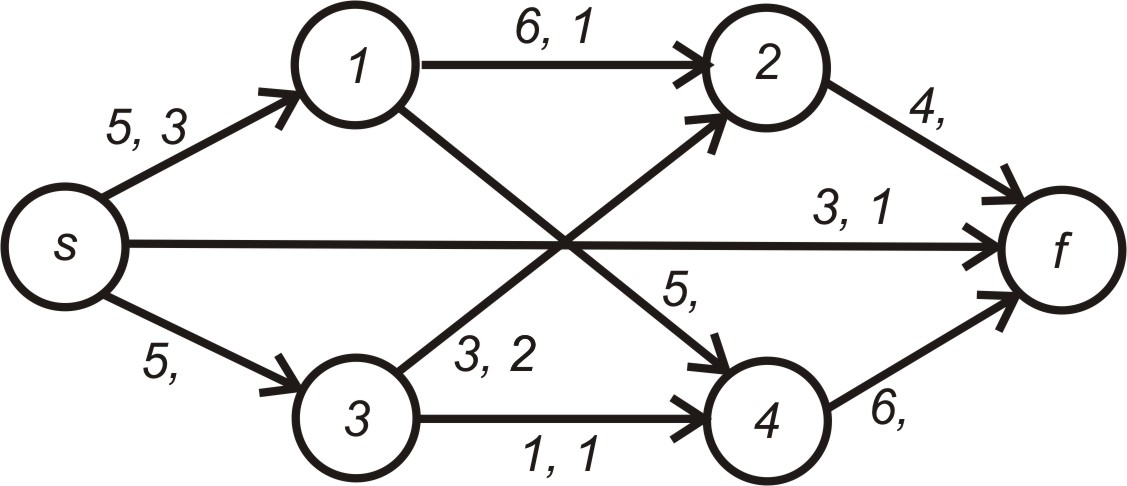
б)
- 5, 3;
- 4, 3;
- 5, 2;
- 6, 3
83. Довжиною ланцюга називається
а) сума
довжин
84. Алгоритм пошуку найкоротшого ланцюга у мережі закінчує свою роботу тоді, коли число дуг, включених до дерева дорівнює
в)
85. В
алгоритмі про максимальний потік, якщо
стік має мітку
,
то потік
замінюємо на
б)
86. В
алгоритмі про максимальний потік, якщо
стік має мітку
,
то потік
замінюємо на
а)
87. В
алгоритмі про максимальний потік кожному
вузлу присвоюється мітка
,
де
в)
88. Мітка для вузла мережі має такий вигляд: . Друга частина мітки означає:
а) резерв
вершини
89. На рисунку показана мережа після виконання першого кроку в алгоритмі знаходження максимального потоку.
Після другого кроку потоки по дугам набудуть такого значення:
г)
;
;
;
;
90. Алгоритм Форда-Фолкерсона закінчується тоді коли:
б)
91. На
кроці 3 алгоритм Форда-Фолкерсона має
такий зміст: якщо
не відмічений, (
)
– дуга і
.
Покласти
в)
.
Встановити
попередника вузла
в
.
Якщо
,
добавити
в
.
92. На
кроці 4 алгоритм Форда-Фолкерсона має
такий зміст: якщо
не відмічений, (
)
– дуга і
.
Покласти
а)
.
Встановити попередника вузла в ; добавити в .
93. Функція
передування після виконання чергового
кроку в алгоритмі Форда-Фолкерсона має
такий вигляд:
.
Резерв стоку дорівнює 3. Який вигля буде
мати функція передування після виконання
наступного кроку
в)
94. Функцію передування в алгоритмі Форда-Фолкерсона утворюють
г) вилучені із множини вузли + стік
95. В алгоритмі про найкоротші ланцюги на третьому кроці обчислень виконується така операція:
б)
96. В
алгоритмі про найкоротші ланцюги мітка
називається
а) тимчасовою
97. В
алгоритмі про найкоротші ланцюги мітка
називається
б) постійною
98. Тернарна операція визначається наступним співвідношенням:
а
г)
.
99. При виконанні тернарної операції обсяг обчислень не перевершує
в)
операцій додавання і порівняння.
100. На деякому кроці виконання тернарної операції отримали наступну таблицю:
Реалізувати
наступний етап обчислень, коли
,
.
а) ???
|
В у з л и |
|||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
||
В у з л и |
1 |
0 |
11 |
30 |
23 |
13 |
32 |
|
2 |
11 |
0 |
31 |
12 |
2 |
21 |
|
|
3 |
30 |
31 |
0 |
19 |
30 |
4 |
|
|
4 |
23 |
12 |
19 |
0 |
11 |
9 |
|
|
5 |
13 |
2 |
30 |
11 |
0 |
20 |
|
|
6 |
32 |
21 |
4 |
9 |
20 |
0 |
|
|
7 |
43 |
32 |
39 |
20 |
1 |
1 |
0 |
|
б)
в)
101. У системі масового обслуговування з кінцевим числом станів, станами системи є:
б) число обслуговуючих приладів + кількість заявок у черзі
102.
Ергодичний розподіл системи масового
розподілу типу
M/M/N/n
буде
таким:
г)
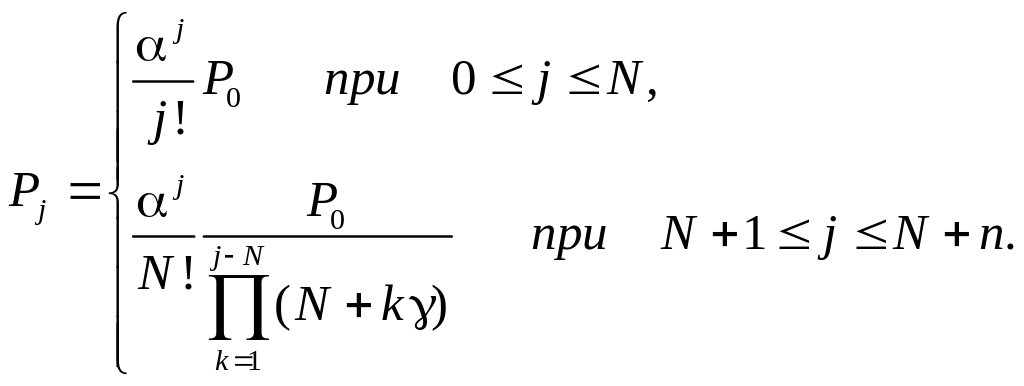
103.
Марківський
процес
називається ергодичним, якщо
а)
.
б)
104.
Математична модель СМО типу
M/M/N/n
для значень
буде
такою:
в)
105. .
Математична модель СМО типу
M/M/N/n
для значень
буде такою:
г)
106. Для
СМО типу M/M/N
з нескінченим числом місць у буфері
ергодичні ймовірності існують, якщо
між параметрами системи
існують такі співвідношення:
б)
,
,
,
в
107. Ерготичні розподіли системи МО типу M/M/N/n без обмежень на тривалість перебування в черзі обчислюються за формулами
а)
108. Для системи МО типу M/M/N/n інтенсивності переходів визначаються такою формулою:
б)
109. Коли система МО типу M/M/1/0, має один обслуговуючий прилад, то
г)
110. Коли система МО типу M/M/1/0, має один обслуговуючий прилад, то
в)