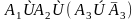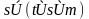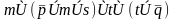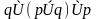2.3.2 Нормальные формы

Определение. Элементарной конъюнкцией п высказываний называется конъюнкция высказываний или их отрицаний.

Определение. Элементарной дизъюнкцией п высказываний называется дизъюнкция высказываний или их отрицаний.

Теорема 1. Чтобы элементарная дизъюнкция была тождественно истинной, необходимо и достаточно, чтобы в ней содержалось два высказывания, из которых одно является отрицанием другого.

Теорема 2. Чтобы элементарная конъюнкция была тождественно ложной, необходимо и достаточно, чтобы в ней присутствовала пара высказываний, из которых одно является отрицанием другого.

Определение. Формула равносильная данной и представляющая собой дизъюнкцию элементарных конъюнкций называется дизъюнктивной нормальной формой данной формулы (ДНФ).

Определение. Формула равносильная данной и представляющая собой конъюнкцию элементарных дизъюнкций называется конъюнктивной нормальной формой данной формулы (КНФ).

Определение. Элементарная конъюнкция (дизъюнкция) называется правильной, если в нее каждая переменная входит не более одного раза (включая ее вхождения под знаком отрицания).

Определение. Правильная элементарная конъюнкция (дизъюнкция) называется полной относительно переменных , если каждая из этих переменных входит в нее один и только один раз (может быть, под знаком отрицания).

Пример.

3. Варианты заданий

Вариант 1

Задание 1. Упростить формулы с помощью тождественных преобразований:

а)

б)

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 2

Задание 1. Упростить формулы с помощью тождественных преобразований:

а)

б)

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 3

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 4

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 5

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим ;

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 6

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

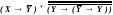
Вариант 7

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 8

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 9

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 10

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 11

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 12

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

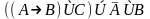
Вариант 13

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 14

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

Вариант 15

Задание 1. Упростить формулы с помощью тождественных преобразований:

1. 

2. 

Задание 2. Определить с помощью тождественных преобразований, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Преобразовать формулу к ДНФ:

Задание 4. Преобразовать формулу к КНФ:

2.5 Вопросы к защите практической работы № 2

1. Какие формулы называются равносильными?

2. Сформулируйте законы логики высказываний.

3. Какие преобразования называются тождественными?

4. Что называется элементарной конъюнкцией?

5. Что называется элементарной дизъюнкцией?

6. Сформулируйте определение КНФ.

7. Сформулируйте определение ДНФ.

3 Практическая работа№3 Совершенная дизъюнктивная нормальная форма и совершенная конъюнктивная нормальная форма

Цель работы: Научится строить СДНФ и СКНФ различными способами.

3.1 Ход работы:

1) изучить теоретический материал по теме практической работы (лекции, учебники);

2) выполнить задание своего варианта;

3) составить отчет по работе;

4) защитить работу.

3.2 Содержание отчета

Отчет по практической работе должен содержать:

1) тему работы;

2) цель работы;

3) ход работы;

4) формулировку заданий;

5) решение заданий своего варианта.

3. Методические указания к практической работе № 3