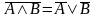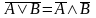1.5 Вопросы к защите практической работы № 1

1) Что называется высказыванием? Приведите примеры высказываний.

2)Что такое - таблица истинности? Как обозначаются значения истинности.

3) Перечислите операции над высказываниями и их обозначения.

4) Сформулируйте определение конъюнкции высказываний.

5) Сформулируйте определение дизъюнкции высказываний.

6) Сформулируйте определение импликации высказываний.

7) Сформулируйте определение эквиваленции высказываний.

8) Что называется отрицанием высказывания? Приведите пример.

9) Что называется логической формулой?

2 Практическая работа №2. Равносильность формул логики высказываний. Дизъюнктивная нормальная форма и конъюнктивная нормальная форма.

Цель работы: Научится применять законы логики высказываний для доказательства равносильности формул и приведения их к ДНФ и КНФ.

2.1 Ход работы:

1) изучить теоретический материал по теме практической работы (лекции, учебники);

2) выполнить задание своего варианта;

3) составить отчет по работе;

4) защитить работу.

2.2 Содержание отчета

Отчет по практической работе должен содержать:

1) тему работы;

2) цель работы;

3) ход работы;

4) формулировку заданий;

5) решение заданий своего варианта.

3. Методические указания к практической работе № 2

2.3.1 Равносильность формул логики высказываний

Определение. Пусть А и В – две формулы, зависящие от одного и того же списка переменных. Будем называть их равносильными, если для любого набора значений переменных они принимают одинаковые значения.

Другой способ доказательства равносильности формул или проверки их тождественной истинности или ложности состоит в использовании так называемых основных логических законов (основных равносильностей), обоснование которых можно провести путем построения соответствующих таблиц истинности. К основным логическим законам обычно относят следующие соотношения:

Рассмотрим основные равносильности логики высказываний.

Пусть А, В, С – произвольные формулы.

Таблица 3 – Основные логические законы

1. Идемпотентность
А  А = А	А  А = А
2. Коммутативность
А  В = В  А	А  В = В  А
3. Ассоциативность
А  (В  С) = (А  В)  С	А  (В  С) = (А  В)  С
4. Правила поглощения
А  (А  В) = А	А  (А  В) = А
5. Дистрибутивность
А  (В  С) = (А  В)  (А  С)	А  (В  С) = (А  В)  (А  С)
6. Правила де Моргана
7. Свойства констант
А  1 = А А  0 = 0	А  0 = А А  1 = 1
8. Закон исключения третьего и закон противоречия
9. Снятие двойного отрицания
10. Формулы расщепления (склеивания)
11. Связь дизъюнкции, конъюнкции, отрицания и импликации
12. Выражение эквивалентности

Определение. Такие преобразования, использующие равносильности формул (запас которых можно расширять с помощью правила подстановки) и правило замены, называются тождественными преобразованиями.

Тождественные преобразования являются мощным средством доказательства равносильности формул и тождественной истинности или тождественной ложности формул, как правило, более эффективным, чем их вычисление на наборах значений переменных (т.е. чем составление таблиц истинности).

Отметим, что «тактика» доказательства равносильности может быть разная: либо преобразуем одну из формул, приводя ее к виду другой, либо преобразуем обе формулы, приводя их к одной и той же формуле.

Примеры.

1. Упростить формулу: .

2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим:

1. ;

2. .

Решение.

1.

2. a)

Поскольку формула при любых значениях переменных равна нулю, то данная формула является противоречием.

b)

Поскольку формула при любых значениях переменных равна единице, то данная формула является тавтологией.