1.4 Варианты заданий

Вариант 1

Задание 1. Разбить высказывание на элементарные и записать в виде формул логики высказываний:

а) «В огороде идет дождь, а в Оренбурге дядька»;

б) «Если неверно, что в огороде идет дождь, то, или в Оренбурге дядька, или в огороде бузина».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Доказать выполнимость формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

1. 

2. 

Вариант 2

Задание 1. Разбить высказывание на элементарные и записать в виде формул логики высказываний:

а) «Функция непрерывна и дифференцируема»;

б) «Если функция не является непрерывной, то она недифференцируема».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Доказать выполнимость формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x → (y ↓ z) и (x → y ) ↓ (x → z)

b) ((x ≡ y) · (x | y)) и x & y

Вариант 3

Задание1. Пусть A – высказывание «Завтра экзамен», B – высказывание «Студент пишет шпаргалки». Сформулировать словесно:

; ;

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Доказать выполнимость формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x → (y ≡ z) и (x → y ) ≡ (x → z)

b) (x → y) и

Вариант 4

Задание 1. Пусть A – высказывание «Завтра экзамен», B – высказывание «Студент пишет шпаргалки». Сформулировать словесно:

; .

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим .

Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x ≡ (y | z) и (x ≡ y) | (x ≡ z)

b) (((x ↓ y)↓( x ↓ y)) ((x ↓ x) )↓( y ↓ y))) и (x y)

Вариант 5

Задание 1. Какой логической операции соответствует употребление «или» в высказываниях:

а) Родители разрешили завести или собаку, или кошку.

б) Кошелек или жизнь!

в) «Если Иван подготовится к экзамену, то он сдаст экзамен успешно и его мама будет довольна».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим ;

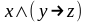Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x ↓ (y | z) и (x ↓ y) | (x ↓ z)

b) (x → z) и (( x (y & z)) →((x y) & z))

Вариант 6

Задание 1.Записать в виде формул логики высказываний, обозначив за переменные элементарные высказывания:

а) «Если функция не является непрерывной, то она недифференцируема»;

б) «Теорема неверна или в доказательстве допущена ошибка».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

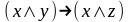
Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x → (y ↓ z) и (x → y) | (x → z)

b) и

Вариант 7

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) «Либо студент сдает сессию, либо его отчисляют»я;

б) «Если в данном четырехугольнике диагонали имеют равную длину, то этот четырехугольник - ромб».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x ↓(y z) и (x ↓y) (x ↓ z)

b) и

Вариант 8

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) «Завтра будет облачно или будет снег и не будет ветра».

б)«Если платина – драгоценный металл, то все птицы летают».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Доказать тождественную истинность формулы

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x (y z) и (x y) (x z)

b) и

Вариант 9

Задание 1. Записать логическими формулами следующее сложное высказывание:

а)«Неверно, что ветер дует тогда и только тогда, когда идет дождь».

б)«Если Волга впадает в Черное море, то белые медведи живут в Африке».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Доказать тождественную истинность формулы

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x → (y ≡ z) и (x → y) ≡ (x → z)

b) и

Вариант 10

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) «Вася получит пять тогда и только тогда, когда защитит лабораторные работы и успешно сдаст экзамен».

б) «Если погода пасмурная, то идет дождь».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x → (y | z) и (x →y) | (x → z)

b)

Вариант 11

Задание 1. Пусть A – высказывание «Сегодня холодно», B – высказывание «Студент идет на занятия». Сформулировать словесно:

; ;

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Доказать тождественную истинность формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a) x | (y z) и (x | y) (x | z)

b)

Вариант 12

Задание 1. Пусть A – высказывание «Сегодня холодно», B – высказывание «Студент идет на занятия». Сформулировать словесно:

; .

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Составить таблицы истинности для формулы

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

a)

b)

Вариант 13

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) Если студент сдает сессию, то его не отчисляют.

б) Если в данном четырехугольнике стороны имеют равную длину, то этот четырехугольник является ромбом или квадратом».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Составить таблицы истинности для формулы

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

1. 

2. 

Вариант 14

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) «Завтра будет облачно, если будет снег или не будет ветра».

б)«Платина – драгоценный метал или все птицы летают».

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Составить таблицы истинности для формулы

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

1. 

2. 

Вариант 15

Задание 1. Записать логическими формулами следующее сложное высказывание:

а) Если студент сдает все экзамены, то его не отчисляют.

б) В данном треугольнике стороны имеют равную длину тогда и только тогда, когда все углы треугольника равны или он прямоугольный.

Задание 2. Определить, является ли формула тавтологией, противоречием или ни тем, ни другим

Задание 3. Составить таблицы истинности для формулы .

Задание 4. Используя таблицу истинности, установить эквивалентность функций в формулах

1. 

2.