2. Логические операции над предикатами.

Предикаты так же, как высказывания, могут принимать два значения: “истина” (1) и “ложь” (0), поэтому к ним применимы все операции логики высказываний, в результате чего из элементарных предикатов формируются сложные предикаты (как и в логике высказываний, где из элементарных высказываний формировались сложные, составные). Рассмотрим применение операций логики высказываний к предикатам на примерах одноместных предикатов. Эти операции в логике предикатов сохраняют тот же смысл, который был им присвоен в логике высказываний.

Пусть на некотором множестве M определены два предиката P(x) и Q(x).

Определение 1. Конъюнкцией двух предикатов P(x) и Q(x) называется новый (сложный) предикат , который принимает значение “истина” при тех и только тех значениях , при которых каждый из предикатов принимает значение “истина”, и принимает значение “ложь” во всех остальных случаях.

Очевидно, что областью истинности предиката является общая часть области истинности предикатов P(x) и Q(x), т.е. пересечение .

Так, например, для предикатов P(x): “x – четное число” и Q(x): “x кратно 3” конъюнкцией является предикат “x – четное число и x кратно трем”, т.е. предикат “x делится на 6”.

Определение 2. Дизъюнкцией двух предикатов P(x) и Q(x) называется новый предикат , который принимает значение “ложь” при тех и только тех значениях , при которых каждый из предикатов принимает значение “ложь”, и принимает значение “истина” во всех остальных случаях.

Ясно, что областью истинности предиката является объединение области истинности предикатов P(x) и Q(x), т.е. .

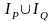Определение 3. Отрицанием предиката P(x) называется новый предикат или , который принимает значение “истина” при всех значениях , при которых предикат P(x) принимает значение “ложь”, и принимает значение “ложь” при тех значениях , при которых предикат P(x) принимает значение “истина”.

Очевидно, что , т.е. множество истинности предиката является дополнением к множеству I_P.

Определение 4. Импликацией предикатов P(x) и Q(x) называется новый предикат 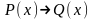, который является ложным при тех и только тех значениях , при которых одновременно P(x) принимает значение “истина”, а Q(x) – значение “ложь”, и принимает значение “истина” во всех остальных случаях.

Поскольку при каждом фиксированном справедлива равносильность , то .

Определение 5. Эквиваленцией предикатов P(x) и Q(x) называется новый предикат , который обращается в “истину” при всех тех и только тех , при которых P(x) и Q(x) обращаются оба в истинные или оба в ложные высказывания.

Для его множества истинности имеем:

4. Варианты заданий

Вариант 1

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝14≥2х˝

В(х): ˝4х+1=17˝, х R

б) F(х;у): ˝х+у=3˝

Q(х;у): ˝х²+(у-2)²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝3х6˝

А(х): ˝х≥-5˝

б) Р(х): ˝2х+111˝

Q(х): ˝2х+3=7˝

Задание 3. Найти области истинности предикатов: , , , , , , 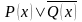заданных на множестве :

,

Вариант 2

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝10≥х˝

В(х): ˝7х-5=16˝, х R

б) F(х;у): ˝х-2у=2˝

Q(х;у): ˝х²+у²≤36˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤12˝

Q(х): ˝х<-10˝

б) Р(х): ˝4+3х13˝

Q(х): ˝7х+8=6˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 3

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝6≥х˝

В(х): ˝3х+4=16˝, х R

б) F(х;у): ˝х-у=2˝

Q(х;у): ˝х²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х9˝

А(х): ˝х≥-2˝

б) Р(х): ˝х+220˝

Q(х): ˝2х+3=17˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 4

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝18≥х˝

В(х): ˝х-4=14˝, х R

б) F(х;у): ˝х+у=3˝

Q(х;у): ˝х²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤10˝

Q(х): ˝х<-5˝

б) Р(х): ˝4+х23˝

Q(х): ˝3х+2=16˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 5

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) В(х): ˝6<х˝

А(х): ˝-2х+3=-9˝, х R

б) F(х;у): ˝х+3у=6˝

Q(х;у): ˝х²+(у-3)²≤25˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х-6˝

А(х): ˝-2х≥4˝

б) Р(х): ˝2-х10˝

Q(х): ˝2х+1=7˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 6

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝13≥х˝

В(х): ˝х+3=11˝, х R

б) F(х;у): ˝х+у=8˝

Q(х;у): ˝х²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤6˝

Q(х): ˝2-х<-2˝

б) Р(х): ˝4-х10˝

Q(х): ˝3х+5=6˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 7

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) В(х): ˝4<х˝

А(х): ˝2х+5=7˝, х R

б) F(х;у): ˝х+у=6˝

Q(х;у): ˝х²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝4х8˝

А(х): ˝6х≥-3˝

б) Р(х): ˝-х-210˝

Q(х): ˝6х+3=7˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 8

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) В(х): ˝9<х˝

А(х): ˝4х+3=7˝, х R

б) F(х;у): ˝2х+у=4˝

Q(х;у): ˝(х-2)²+у²≤25˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤6˝

Q(х): ˝3х+1<-2˝

б) Р(х): ˝3+х13˝

Q(х): ˝4х+2=6˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 9

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝15≥х˝

В(х): ˝2х+4=16˝, х R

б) F(х;у): ˝3х+у=2˝

Q(х;у): ˝(х-3)²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х16˝

А(х): ˝-2х≥-6˝

б) Р(х): ˝3х-210˝

Q(х): ˝5х-3=7˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 10

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝12≥х˝

В(х): ˝х+9=16˝, х R

б) F(х;у): ˝х+5у=2˝

Q(х;у): ˝х²+у²≤64˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤6˝

Q(х): ˝2х<-2˝

б) Р(х): ˝4+2х12˝

Q(х): ˝3х-9=6˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 11

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝20≥2х˝

В(х): ˝3х+12=48˝, х R

б) F(х;у): ˝-х+у=-2˝

Q(х;у): ˝(х-2)²+у²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х4˝

А(х): ˝х≥-2˝

б) Р(х): ˝х+410˝

Q(х): ˝3х+2=8˝

Задание 3. Найди множество истинности для следующих предикатов и их отрицаний:

А (х): «х > 3.5»; В (у): «2у < у»;

D (z): « ».

Для тех предикатов, переменные которых – числа, изобрази соответствующие множества на числовой прямой.

Вариант 12

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝5≥х˝

В(х): ˝х+4=6˝, х R

б) F(х;у): ˝3х+у=2˝

Q(х;у): ˝х²+(у-4)²≤16˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤4˝

Q(х): ˝х<-8˝

б) Р(х): ˝4+х10˝

Q(х): ˝3х+9=6˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 13

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) В(х): ˝6<х˝

А(х): ˝2х+3=7˝, х R

б) F(х;у): ˝х+у=4˝

Q(х;у): ˝х²+у²≤25˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х8˝

А(х): ˝х≥-5˝

б) Р(х): ˝х+215˝

Q(х): ˝2х+3=17˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 14

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) А(х): ˝11≥х˝

В(х): ˝х+5=15˝, х R

б) F(х;у): ˝х+2у=2˝

Q(х;у): ˝х²+у²≤9˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х≤5˝

Q(х): ˝-х<2˝

б) Р(х): ˝4+х11˝

Q(х): ˝3х+2=8˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,

Вариант 15

Задание 1. Найти множество истинности коньюнкции двух предикатов

а) В(х): ˝7<х˝

А(х): ˝2х+4=8˝, х R

б) F(х;у): ˝х+2у=4˝

Q(х;у): ˝х²+у²≤4˝, х R

Задание 2. Найти множество истинности дизъюнкции двух предикатов

а) Р(х): ˝х6˝

А(х): ˝х≥-3˝

б) Р(х): ˝х+210˝

Q(х): ˝2х+3=5˝

Задание 3. Найти области истинности предикатов: , , , , , , заданных на множестве :

,