4. Свойства теоретико-множественных операций

Для произвольных множеств А, В, и С справедливы следующие соотношения (табл. 7):

Таблица 7 – Свойства теоретико-множественных операций

1. Коммутативность объединения	1’. Коммутативность пересечения
2. Ассоциативность объединения	2’. Ассоциативность пересечения
3. Дистрибутивность объединения относительно пересечения	3’. Дистрибутивность пересечения относительно объединения
4. Законы действия с пустым и универсальным множествами	4’. Законы действия с пустым и универсальным множествами
5. Закон идемпотентности объединения	5’. Закон идемпотентности пересечения
6. Закон де Моргана	6’. Закон де Моргана
7. Закон поглощения	7’. Закон поглощения
8. Закон склеивания	8’. Закон склеивания
9. Закон Порецкого	9’. Закон Порецкого
10. Закон двойного дополнения

Пример.

Доказать следующее тождество .

Решение.

Докажем это тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна).

1.

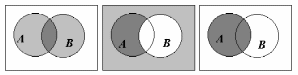
2. Построим соответствующие диаграммы Эйлера-Венна (рис. 7).

Рис. 7.

3. Варианты заданий

Вариант 1

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = [-3; 0] – отрезок числовой оси

В = (-1; 3] – полуинтервал на числовой оси

С = (-0.5; 4) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 2

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (0; 10] – полуинтервал на числовой оси

В = [–1; 5] – отрезок числовой оси

С = (–10; 2) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 3

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = {0, 1, 2, 3}– четырехэлементное множество

В = [–5; 3] – отрезок числовой оси

С = (0; 2) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 4

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–1; +∞)– интервал на числовой оси

В = (–10; 10] – полуинтервал на числовой оси

С = [–5; +15] – отрезок числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 5

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–16; 8]– полуинтервал на числовой оси

В = [–9; 9] – отрезок числовой оси

С = (5; +∞) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 6

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = [–25; 1]– отрезок числовой оси

В = {–1; 0; 1} – трехэлементное множество

С = (0; +∞) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 7

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–10; 5]– полуинтервал на числовой оси

В = [0; 10] – отрезок числовой оси

С = (4; +∞) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 8

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–∞; 2]– полуинтервал на числовой оси

В = [–3; 3] – отрезок числовой оси

С = (0; 4) – интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

; .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 9

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–2; 3) – интервал на числовой оси

В = [0; 4] – отрезок числовой оси

С = {2; 3} – двухэлементное множество

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

.

Вариант 10

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = [–7.5; 4.5]– отрезок числовой оси

В = (0; 5)– интервал на числовой оси

С = (–10; 0] – полуинтервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

Вариант 11

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–5; 5]– полуинтервал на числовой оси

В = (0; +∞)– интервал на числовой оси

С = {–1; 0; 1} – трехэлементное множество

Задание 2. Докажите тождества, используя только определение операций над множествами.

; .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

Вариант 12

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (–12; 12)– интервал на числовой оси

В = [10; 20] – отрезок числовой оси

С = (–∞; +15] - полуинтервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

Вариант 13

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (5; 15] – полуинтервал на числовой оси

В = [5; 10] – отрезок числовой оси

С = {4; 5; 6} – трехэлементное множество

Задание 2. Докажите тождества, используя только определение операций над множествами.

; .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

_(АВ)А = (АВ)А = А

Вариант 14

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = (0; + ∞) – интервал на числовой оси

В = [–3; 3] – отрезок числовой оси

С = (–10; 0] - полуинтервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.

Вариант 15

Задание 1. Для заданных множеств А, В и С найдите:

АВ, АС, ВС, АВС, АВ, АС, ВС, АВС, A \ B, B \ A, A \ C, C \ A, B \ C, C \ B, (А \ В) \ С, А \ (В \ С), А  B, А  С, B  C, A  B  C. Изобразите на плоскости АВ, АС, ВС. Найдите считая универсальным множеством множество ℝ – всех вещественных чисел (всю числовую ось).

А = [–5; 25) – полуинтервал на числовой оси

В = [–25; 5] – отрезок числовой оси

С = (–10; 15) - интервал на числовой оси

Задание 2. Докажите тождества, используя только определение операций над множествами.

, .

Задание 3. Доказать тождество двумя способами: аналитически (используя равносильности алгебры множеств) и конструктивно (используя диаграммы Эйлера-Венна). В противном случае, докажите, что оно неверно.