Выполнение арифметических операций над числами, представленными с фиксированной запятой.
Основной особенностью различных методов выполнения арифметических операций является то, что любая операция (сложение, вычитание, умножение, деление и др.) сводится к некоторой последовательности микроопераций, таких как:
сложение
сдвиг
передача
преобразование кодов.
Сложение выполняется по правилам сложения чисел в позиционных системах счисления.
То есть эта операция выполняется поразрядно, а возникающий в младших разрядах перенос направляется в старшие разряды.
Пример:
0,101101 1-ое слагаемое
+0,000101 2-ое слагаемое
0,101000 сумма
0,00101 перенос
0,100010 сумма
0,01 перенос
0,110010 сумма
Операции сложения производятся одновременно над всеми разрядами двух слагаемых и продолжаются до тех пор, пока возникают переносы. Возникающие переносы приводят к продолжению операции. Это одна из особенностей позиционных систем. Видим, что собственно операция определения частичной суммы слагаемых выполняется в один приём, а возникающие переносы распространяются на всё более старшие разряды.
Сдвиг.
Различают два вида микрооперации сдвига:
логический сдвиг;
арифметический сдвиг;
Логический сдвиг приводит к смещению всех разрядов числа, включая и знак, влево или вправо. При этом освобождающиеся разряды заполняются нулями или единицами.
Арифметический сдвиг выполняется над частью числа, часть сдвинутых разрядов теряется. (Очевидно, знаковый разряд должен исключаться из рассмотрения).
Передача.
Эта микрооперация предполагает, что некоторый код (число) записывается в соответствующее устройство и вытесняет тот код, который там находился до передачи.
Различают два вида передач:
запись (с разрушением ранее записанной информации);
чтение (без разрушения).
Преобразование.
Функция, выполняемая над передаваемыми числами, называется преобразованием. Чаще других в арифметических основах рассматривают инвертирование кода. Это поразрядная микрооперация yi = xi 1 (1 i n), которая выполняется над всеми разрядами одновременно.
Модифицированные коды
Важная особенность рассмотренных кодов состоит в том, что в процессе выполнения операции сложения-вычитания не происходит переполнения цифровой части числа и переноса в знаковый разряд. Переполнение возникает лишь в знаковом разряде. Так бывает потому, что сумма двух слагаемых по модулю меньше единицы.
При решении реальных задач часто трудно определить заранее, будет ли сумма двух слагаемых меньше единицы. Во всяком случае, для предотвращения переполнения можно вводить дополнительные ограничения на величину слагаемых, сужающих диапазон чисел, с которыми оперирует машина. И то, и другое является неприемлемым.
Рассмотрим такой пример:
X = -0,101 Дополнительный код 1.011 = [X]дк
Y= -0,111 1.001 = [Y]дк
S- = X- + Y- 1| 0.100 = [S]дк
То есть получаем неправильный результат как по знаку, так и в цифровой части.
Рассмотрим ещё один пример:
X = +0,101 В любом из ранее рассмотренных 0.101 = [X]дк,ок
Y = +0,111 кодов имеем 0.111 = [Y]дк,ок
S+ = X+ + Y+, 1.100 = [S]дк,ок
То есть и в этом случае происходящее переполнение в цифровой части искажает результат операции. Можно заметить, что переполнение числовой сетки происходит случае одинаковых знаков слагаемых, так как именно в этом случае модуль результата превосходит модули каждого из слагаемых, сам факт переполнения может быть зафиксирован изменением знака результата.
Таким образом, одним из способов фиксации переполнения является автоматическое определение перехода от одинаковых знаков слагаемых к противоположному знаку результата.
Однако такой способ фиксации переполнения неудобен, так как предварительно знаки слагаемых должны быть запомнены, сравнены между собой и после получения результата.
Существует другой принцип фиксации переполнения. Этот принцип основан на применении так называемых модифицированных кодов. Очевидно, что при переполнении разрядной сетки вычисления необходимо прекратить или, по крайней мере, выработать специальный признак переполнения, а решение о прекращении вычислений возложить на программиста.
Существо модифицированных кодов состоит в том, что к знаковому разряду добавляется ещё один разряд:
"+" ставится в соответствие 00
"–" ставится в соответствие 11
Тогда, по определению модифицированным дополнительным кодом числа называется
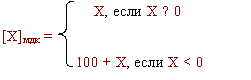
Возникающий в знаковых разрядах перенос теряется. В целом же модифицированный код не отличается от простого дополнительного кода. Аналогично, по определению, обратным кодом является:
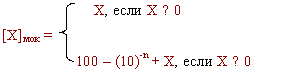
Как и в случае простого обратного кода, возникающая единица переноса в знаковых разрядах по цепи циклического переноса добавляется в младший разряд цифровой части числа.
Так как в сложении по-прежнему участвуют только числа меньше единицы, то
S = X + Y < 2
Поэтому старший знаковый разряд не может быть искажён переносом из цифровой части числа, с другой стороны, перенос, возникающий при сложении чисел в случае, когда
S = X + Y > 1
искажает младший знаковый разряд.
Несовпадение знаковых разрядов после выполнения операции указывает на факт наличия переполнения.