Обратный код.
Обратным называется код, для которого в знаковом разряде положительного числа пишется "0", в цифровых - модуль числа, а для отрицательного - в знаковом разряде пишется единица, в цифровых - инвертированные разряды исходного числа.
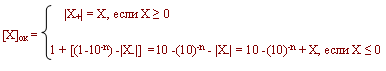
Определим диапазон чисел:
X+ min = 0,00…0 - положительный нуль.
X+ max = 0,111…1 = 1 - 2-n
X- min = 1,11…1 0 = 2 - 2-n+1
X- max = 1,00…00 = 1
В обратном коде есть два изображения нуля:
"Положительный" нуль:
[X]ок = 0,0…0
и "отрицательный" нуль:
[X]ок = 1,11…11
При этом
X - X = [X+]ок + [X-]ок = |X+| + 10 - (10)-n - |X-| = +10 - (10)-n = 0
или 10 ~ (10)-n
То есть, единица переноса в знаковом разряде эквивалентна единице младшего разряда. Поэтому при выполнении операции сложения-вычитания необходимо возникающий перенос циклически прибавлять в младший разряд частичного результата.
Рассмотрим прежние четыре случая, помня о том, что сумма двух слагаемых по модулю должна быть меньше единицы.
X+ = 0,10
Y- = -0,01
X+ + Y- = S+
В обратном коде:
Возникающее переполнение должно быть добавлено к младшему разряду частичной суммы.
X+ = 0,10
Y+ = +0,01
X+ + Y+ = S+
В обратном коде:
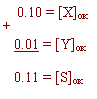
Нет никаких особенностей по сравнению с прямым кодом.
X+ = 0,01
Y- = -0,10
X+ + Y- = S-
В обратном коде:
То есть, не возникает циклического переноса.
X- = -0,01
Y- = -0,10
X- + Y- = S-
В обратном коде:
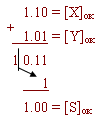
Возникает переполнение знакового разряда, которое добавляется в младший разряд частичной суммы.
Заметим, что получение обратного кода проще, чем дополнительного. Это поразрядно выполняемая микрооперция инверсии кода. Как станет ясно из схемного решения, эта микрооперация выполняется так же быстро, как и передача кода.
Поскольку результатом операции является совокупность результатов по всем разрядам, то данную операцию можно выполнять одновременно под всеми цифровыми разрядами числа.
Дадим практический метод получения двоичного числа в дополнительном коде (без математического обоснования):
проинвертировать все биты исходного числа;
к полученному результату прибавить 1(или другими словами проинвертируем все цифры вплоть до последнего разряда).
Пример:
Пусть требуется получить двоичное значение десятичного числа: - 510. Формат числа 16-ти разрядное слово.
Итак:
510 = 0000 0000 0000 0101
инверсия 1111 1111 1111 1010
добавим +1, получим требуемое двоичное число, эквивалентное -510
1111 1111 1111 10112
Здесь необходимо особое внимание уделять старшему разряду, он называется «знаковым».
0 – для знака плюс и 1 – для знака минус. При определении величины числа знак разряда не используется, т.е. мы имеем 15-ти разрядное двоичное число. Сложение двоичного числа с его дополнительным кодом всегда дает нулевой результат.
Таким образом, можно сказать, что если исходное число положительное, то в знаковый разряд записываем «0», а информационную часть числа записываем без изменений.
Если число отрицательное, тогда в знаковый разряд записываем «1», а информационную част числа инвертируем до последней значащей цифры.
Иногда находит применение обратный код. Что касается положительного числа, то здесь правила записи не отличаются от правил записи чисел в прямом и обратном коде. Если число отрицательное, то в знаковый разряд записывается «1», а информационная часть числа полностью инвертируется.
Однако, двоичная запись числа не всегда удобна (длинная), поэтому в компьютерной технике часто применяют сокращенную нотацию двоичных чисел – восьмеричную и шестнадцатеричную системы счисления.
Вопросы и задания:
1. Преобразуйте (1001101001)2 в Х10, Х8 и Х16.
2. Примеры на действия с двоичными числами.