
- •Семинар 1. Числовой логический уровень
- •Система счисления.
- •Позиционные системы счисления.
- •Выбор системы счисления
- •Перевод чисел из одной системы счисления в другую
- •Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.
- •Проблема представления отрицательных чисел
- •Прямой код.
- •Замечания.
- •Дополнительный код.
- •Обратный код.
- •Способы представления чисел в эвм
- •Фиксированная запятая
- •Плавающая запятая
- •Выполнение арифметических операций над числами, представленными с фиксированной запятой.
- •Семинар 2. Цифровой логический уровень и микроархитектурный уровень
- •Электротехническая интерпретация.
- •У ровень физических устройств.
- •Дешифратор
- •Шифратор
- •Регистр сдвига
- •Методы передачи данных
- •Параллельная передача данных
- •Последовательная передача данных
- •Синхронные коммуникации
- •Передача в основной полосе частот и широкополосная передача.
- •Вопросы и задания
- •Семинар 3. Архитектура классической эвм
- •Система кодирования команд
- •Взаимозависимость формата команды и основных параметров эвм
- •Способы адресации
- •Семинар 4. Простой процессор, работающий с четырехадресной командой. Введение
- •Функционирование программируемого процессора
- •Алгоритм работы
- •Задание
- •Семинар 5. Микропроцессор – дальнейшее развитие Введение
- •Модернизация
- •Задание
- •Семинар 6. Дальнейшее совершенствование микропроцессора, одноадресные и безадресные команды. Анализ предыдущей модели
- •Задание
- •Шинная структура связей
- •Семинар 7. Кэш-память Введение
- •Структура кэш-памяти в процессоре i486.
- •Алгоритм псевдо lru.
- •Увеличение производительности кэш памяти.
- •Семинар 8. Режимы работы микропроцессорной системы
- •Архитектура микропроцессорных систем
- •Типы микропроцессорных систем
- •Семинар 9 . Программная модель процессора
- •Общие понятия
- •Регистры процессора
- •Формат команды микропроцессора ia-32
- •Эффективный адрес.
- •Семинар 10. Организация пк Введение
- •Архитектура персонального компьютера
- •Процессоры персональных компьютеров
- •Особенности процессоров Pentium
- •Семинар 11. Интерфейсы пк Введение
- •Последовательный порт(rs-232).
- •Параллельный порт(lpt).
- •Интерфейс ide.
- •Cпецификация Enhanced ide (eide)
- •Интерфейс scsi.
- •Характеристики scsi.
- •Системная магистраль isa
- •Распределение ресурсов компьютера
- •Семинар 12. Видеосистема пк и режимы графической акселерации Введение
- •Мониторы
- •Видеоадаптеры
- •Понятие о графических ускорителях
- •Ускорители двумерной графики
- •Ускорители трехмерной графики
- •Семинар 13. Файловая система компьютера Введение
- •Общие сведения о файлах
- •Типы файлов
- •Атрибуты файлов
- •Организация файлов и доступ к ним
- •Последовательный файл
- •Файл прямого доступа
- •Другие формы организации файлов
- •Операции над файлами
- •Директории. Логическая структура файлового архива
- •Разделы диска. Организация доступа к архиву файлов.
- •Операции над директориями
- •Защита файлов
- •Контроль доступа к файлам
- •Списки прав доступа
- •Заключение
- •Семинар 14. Практика настройки и использования пк. Системный блок
- •Загрузка операционной системы
- •Дисковые накопители
- •Настройка компьютера
- •Настройка видеоадаптера
- •Настройка звуковой карты
- •Настройка cd-rom
- •Защита данных и самого компьютера
- •Использование программы bios setup
- •Модернизация компьютера
- •Увеличение оперативной памяти
- •Установка дополнительных плат
- •Самотестирование при включении
- •Поиск и устранение неисправностей
- •Системная плата
- •Основной микропроцессор
- •Системная и локальная шина.
Перевод чисел из одной системы счисления в другую, когда одно основание является целой степенью другого.
Как мы уже знаем, в ЭВМ наибольшее применение находит система с основаниями 2, 4, 8, 16, т.е. системы которые кратны степени 2. Поэтому целесообразно рассмотреть лишь правила перевода чисел в этих системах. Аналогичные правила будут справедливы и для других систем. Допустим, что имеется некоторое целое число N8 в 8-ой системе. Оно может быть представлено в виде:
N8 = a1*8n-1 + a2*8n-2 + a3*8n-3 + ...
+ an-2*82 + an-1*81 + an*80.
Пусть каким-либо образом мы получили запись этого числа в виде двоичного, т.е.:
N2 = b1*2k-1 + b2*2k-2 + ...
+ bk-2*22 + bk-1*21 + bk*20.
Разделим эти выражения на 23 = 8:
a1*8n-2 + a2*8n-3 + a3*8n-4 + ... + an-1*80 + an*8-1
-------
дробная часть
b1*2k-4 + b2*2k-5 + ... + bk-3*20 + bk-2*2-1 + bk-1*2-2 + bk*2-3
-------------------------
дробная часть
Так как числа были равны, то получается одинаковые частные и одинаковые остатки:
an*8-1 = bk-2*2-1 + bk-1*2-2 + bk*2-3.
Если снова разделим целые части на 23 = 8, то опять получим равные частные и равные остатки.
При этом видим, что каждой восьмеричной цифре соответствует её двоичный эквивалент. Поэтому перевод выполняется простой заменой цифры восьмеричной системы её двоичным эквивалентом и обратно.
Пример:
62,7538 = 110010,1111010112
Аналогично для 4-ой системы:
321,22334 = 111001,101011112
Аналогично для 16-ой системы:
1D876,72 = 00011101100001110110,011100102
Из этих примеров видим, что чем выше основание системы счисления, тем компактнее запись.
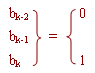
bk-2 |
bk-1 |
bk |
an |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
1 |
0 |
2 |
0 |
1 |
1 |
3 |
1 |
0 |
0 |
4 |
1 |
0 |
1 |
5 |
1 |
1 |
0 |
6 |
1 |
1 |
1 |
7 |
Если умножить последние соотношения на 8, то:
an*8-1*8 = (bk-2*2-1 + bk-1*2-2 + bk*2-3)*23
an = bk-2*22 + bk-1*21 + bk*20
Практически перевод двоичного числа в восьмеричное, шестнадцатеричное и обратно очень прост. Покажем это на примере:

 3 5 0 6 тетрады
350616
3 5 0 6 тетрады
350616
0 0 1 1 0 1 0 1 0 0 0 0 0 1 1 0
0 1 1 0 1 0 1 0 0 0 0 0 1 1 0
3 2 4 0 6 триады 324068
Все позиционные системы одинаковы, в том смысле, что арифметические действия выполняются по одним и тем же правилам.
Пример 2.




1 6-теричное
4 D 1
3 A 5 E
6-теричное
4 D 1
3 A 5 E
2 -ичное
0 1 0 0 1 1 0 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0
1 1 1 1 0
-ичное
0 1 0 0 1 1 0 1 0 0 0 1 0 0 1 1 1 0 1 0 0 1 0
1 1 1 1 0
8-ричное 4 6 4 2 3 5 1 3 2
Пример 3
(11010011)2 = Х10
(17)10 =Х2
