13

НАЦІОНАЛЬНИЙ АВІАЦІЙНИЙ УНІВЕРСИТЕТ

Теорія інформації та кодування

Лекція № 4.2

Технології кодування із компресією даних. Оптимальні нерівномірні коди

2013

Вступ

В попередній лекції були розглянуті оптимальні коди Шеннона-Фано для компресії інформаційних об‘єктів, які дають змогу одержати як рівномірні так нерівномірні коди. Оскільки рівномірні оптимальні коди Шеннона-Фано не дають виграшу в стиснені даних, будемо в подальшому орієнтуватися на нерівномірні коди. Звернемо, окрім того увагу на те, що при побудові кодів цього типу слід мати такі імовірності генерації відповідних символів, що є дробовими числами із знаменниками, ступенями, які є ступенями основи коду ( , S = 1,2, …). Зрозуміло, що такі ситуації є вкрай малоймовірними.

Таким чином, при усій привабливості оптимальних кодів Шеннона-Фано слід використовувати інші нерівномірні коди із довільними значеннями ймовірностей можливих символів, що генеруються відповідним джерелом. Однією із таких технологій є код Хафмена, який розглядається в цій лекції разом із іншими технологіями.

Лекція № 4.2 − “Технології кодування із компресією даних. Оптимальні нерівномірні коди”. В лекції будуть розглянуті наступні учбові питання:

Вступ 2

1. Оптимальні нерівномірні коди. Код Хафмена 3

3. Технології стиснення даних в телекомунікаціях 9

1. Оптимальні нерівномірні коди. Код Хафмена

Алгоритм Хафмена є деревоподібним кодом, заснованим на статистичному кодуванні, тобто на кодування, яке враховує статистичні характеристики символів, тобто імовірності їх існування в усіх можливих повідомленнях.

Деревоподібним кодом називають код, кодовими словами якого є тільки ті, що відповідають кінцевим вершинам кодового дерева.

Кодове дерево – спеціальний граф, що відображає запис всіх можливих S-кових n-розрядних чисел, використовуваних як кодові комбінації для кодування повідомлень в кількості M = Sⁿ. При цьому кожне число відображається одним з вузлів графа. З кожного вузла виходить S гілок, які пов’язують цей вузол з іншими. Кількість символів, що входять до числа, відповідного даному вузлу, називається його порядком.

Розглянемо граф для двійкового трьохелементного коду (рис. 3).

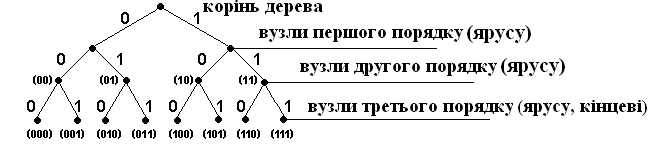
1. Кодове дерево двійкового трьохелементного коду

На початковому (нульовому) ярусі розташований один вузол, який називається коренем дерева.

Кінцевим вузлом називається вузол, якщо з нього не виходить жодного ребра.

Для побудови оптимального коду на базі кодового дерева треба дотримуватися наступного:

• повідомленню з найбільшою імовірністю повинен відповідати вузол якнайменшого порядку;

• принаймні два повідомлення з мінімальною імовірністю повинні кодуватися вузлами максимального порядку;

• якщо вибрано деякий вузол порядку і, то всі вузли вищого порядку, пов’язані з ним, не можуть бути використані для кодування, інакше не виконуватиметься однозначна відмінність комбінацій, заснована на тому, що жодна з них не повинна бути початком іншої;

• для кодування повідомлень можуть не бути використані всі можливі вузли максимального порядку; це означає, що не всі вузли попереднього порядку є повними (повним називається вузол, з якого виходять всі можливі S гілок);

• якщо об’єднати всі повідомлення, закодовані вузлами і-го порядку, то вузлу (і – 1) – го порядку відповідатимуть повідомленню з еквівалентною імовірністю

.

Реалізація коду Хафмена

Хай є джерело даних, яке передає символи з різним ступенем імовірності, тобто кожному відповідає своя імовірність (або частота) , причому існує хоча б одна пара і , , такі, що і не рівні. Таким чином утворюється набір частот при чому , оскільки передавач не передає більше ніяких символів окрім як .

Наша задача – підібрати такі кодові символи з довжинами щоб середня довжина кодового символу не перевищувала середньої довжини початкового символу. При цьому потрібно враховувати умову, що якщо і , то .

Хафмен запропонував будувати дерево, в якому вузли з найменшою імовірністю якнайдальше віддалені від кореня. Звідси і витікає алгоритм побудови дерева чи алгоритм кодування:

1. Вибрати два символи і , такі, що і зі всього списку є мінімальними.

2. Звести гілки дерева від цих двох елементів в одну точку з імовірністю , помітивши одну гілку нулем, а іншу – одиницею (за власним розсудом).

3. Повторити пункт 1 з урахуванням нової точки замість і , якщо кількість точок, що вийшли, більше одиниці. Інакше ми досягли кореня дерева.

Приклад. Тепер спробуємо скористатися одержаною теорією і закодувати інформацію, передану джерелом, на прикладі семи символів.

Розберемо детально перший цикл. На малюнку зображена таблиця, в якій кожному символу і відповідає своя імовірність (частота) .

Згідно пункту 1 ми вибираємо два символи з таблиці з якнайменшою імовірністю. У нашому випадку це і . Згідно пункту 2 зводимо гілки дерева від і у одну точку і позначаємо гілку, що веде до , одиницею, а гілку, що веде до , – нулем. Над новою точкою приписуємо її імовірність (в даному випадку - 0.03). Надалі дії повторюються вже з урахуванням нової точки і без урахування і .

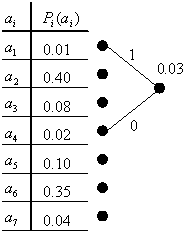
Після багатократного повторення висловлених дій будується наступне дерево:

По побудованому дереву можна визначити значення кодів , здійснюючи спуск від коріння до відповідного елементу , при цьому приписуючи до одержуваної послідовності при проходженні кожної гілки нуль або одиницю (залежно від того, як іменується конкретна гілка). Таким чином таблиця кодів виглядає таким чином:

1	0,01	011111	6
2	0,40	1	1
3	0,08	0110	4
4	0,02	011110	6
5	0,10	010	3
6	0,35	00	2
7	0,04	01110	5

Тепер спробуємо закодувати послідовність з символів.

Хай символу відповідає (як приклад) число і. Хай є послідовність 12672262. Потрібно одержати результуючий двійковий код.

Для кодування можна використовувати таблицю кодових символів із врахуванням, що відповідає символу . У такому разі код для цифри 1 буде послідовністю 011111, для цифри 2 – 1, для цифри 6 – 00, а для цифри 7 – 01110. Таким чином, одержуємо наступний результат:

Дані	12672262	Довжина коду
Початкові	001 010 110 111 010 010 110 010	24 біт
Кодовані	011111 1 00 01110 1 1 00 1	19 біт

В результаті кодування ми виграли 5 біт і записали послідовність 19 бітами замість 24.

Ентропію для нашого випадку:

.

Ентропія має чудову властивість: вона дорівнює мінімальній допустимій середній довжині кодового символу у бітах. Сама ж середня довжина кодового символу обчислюється по формулі:

.

Підставляючи значення у формули і , одержуємо наступні результати:

,

.

Величини і дуже близькі, що говорить про реальний виграш у виборі алгоритму. Тепер порівняємо середню довжину початкового символу і середню довжину кодового символу через коефіцієнт стиснення – відношення початкової довжини символу до середньої довжини стисненого символу :

.

Таким чином, ми одержали стиснення в співвідношенні 1:1,429, що дуже непогане.

І наприкінці, вирішимо останню задачу: дешифровка послідовності бітів.

Хай для нашої ситуації є послідовність бітів:

001101100001110001000111111.

Необхідно визначити початковий код, тобто декодувати цю послідовність.

Звичайно, в такій ситуації можна скористатися таблицею кодів, але це достатньо незручно, оскільки довжина кодових символів непостійна. Набагато зручніше здійснити спуск по дереву (починаючи з коріння) за наступним правилом:

1. Початкова точка – корінь дерева.

2. Прочитати новий біт. Якщо він нуль, то пройти по гілці, поміченій нулем, інакше - одиницею.

3. Якщо точка, в яку ми потрапили, кінцева, то ми визначили кодовий символ, який слідує записати і повернутися до пункту 1. Інакше слід повторити пункт 2.

Розглянемо приклад декодування першого символу. Ми знаходимося в точці з імовірністю 1,00 (коріння дерева), прочитуємо перший біт послідовності і відправляємося по гілці, поміченій нулем, в точку з імовірністю 0,60. Оскільки ця точка не є кінцевою в дереві, то прочитуємо наступний біт, який теж рівний нулю, і відправляємося по гілці, поміченій нулем, в точку , яка є кінцевою. Ми дешифрували символ – це число 6. Записуємо його і повертаємося в початковий стан (переміщаємося в коріння).

Таким чином декодована послідовність приймає вигляд.

Дані	001101100001110001000111111	Довжина коду
Кодовані	00 1 1 0110 00 01110 00 1 00 011111 1	27 біт
Початкові	6 2 2 3 6 7 6 2 6 1 2	11∙3=33 біт

В даному випадку виграш склав 6 біт при достатньо невеликій довжині послідовності.

Слід зазначити, що метод Хафмена застосовний для джерела повідомлень, що з’являються з будь-якою імовірністю, а не тільки з імовірністю цілого ступеня основи коду.

Приклад 2. Задано ансамбль повідомлень:

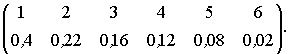
Побудувати двійковий код Хафмена.

Кодове дерево для даного коду представлене на рис. 2.