2.5. Питання для самостійної роботи

1. Швидкості та прискорення двох точок тіла за весь час його руху однакові за модулями і напрямами. Чи можна стверджувати, що дане тіло рухається поступально?

2. Траєкторії всіх точок тіла є колами. Чи можна стверджувати, що тіло здійснює обертальний рух; поступальний рух?

3. Тіло обертається рівномірно. Чи можна стверджувати, що для всіх його точок ?

4. Прискорення яких точок тіла, що обертається: а) мають рівні модулі; б) мають однакові напрями; в) однакові за модулем і напрямом?

5. Чи можливо таке обертання тіла навколо нерухомої осі, при якому вектори швидкості та прискорення довільної точки тіла взаємно перпендикулярні? Спрямовані по одній прямій?

6. Чи можна визначити, що обертання тіла прискорене або уповільнене, за знаком тільки або тільки ?

7. Вектор прискорення точок диска, що обертається, спрямований під кутом до його радіуса. Яке співвідношення між модулями кутової швидкості та кутового прискорення цього диска?

8. Як перевести кутову швидкість, яка виражена в об/хв, у рад/сек?

9. Як спрямовані вектори кутової швидкості і кутового прискорення при уповільненому та прискореному обертаннях?

3. ПлоскопаралельНий рух твердого тіла

3.1. Рівняння та характеристики плоскопаралельного руху

тіла

Плоскопаралельним (або плоским) називається такий рух твердого тіла, при якому всі його точки рухаються у площинах, паралельних деякій площині, нерухомій в розглянутій системі відліку.

При такому русі тіла будь-яка пряма, перпендикулярна нерухомій площині П (наприклад, прямі aа, bb' на рис. 3.1), буде здійснювати поступальний рух, отже, всі кінематичні характеристики точок, що лежать на цій прямій, будуть тотожні. Звідси робимо висновок, що для вивчення руху всього тіла досить досліджувати як рухається в площині Оху переріз цього тіла, що утворює деяку плоску фігуру. Тут площина Оху є нерухомою і паралельною площині П.

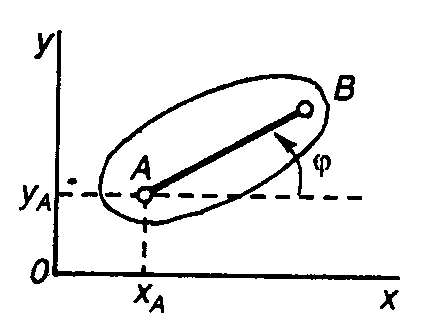
Положення плоскої фігури в площині Оху визначається положенням будь-якого проведеного на цій фігурі відрізка АВ (рис. 3.2). У свою чергу, положення відрізка АВ визначається, наприклад, координатами х_А, у_А точки А та величиною кута між відрізком АВ і віссю х. Точку А, яку вибрано для визначення положення плоскої фігури, називають полюсом.

Закон руху плоскої фігури в її площині, а отже, і плоскопаралельного руху твердого тіла щодо системи координат Оху визначається трьома рівняннями:

. (3.1)

Аналізуючи залежності (3.1), можна зробити висновок, що рух плоскої фігури в її площині є сукупність двох рухів: поступального руху, при якому всі точки рухаються так само, як і полюс А, і обертального руху навколо цього полюса (при цьому фігура обертається навколо осі, що проходить через точку А перпендикулярно площині П).

Рис. 3.1

Рис. 3.2

Основними кінематичними характеристиками плоскопаралельного руху твердого тіла є швидкість і прискорення полюса – характеристики поступальної складової руху), а також кутова швидкість і кутове прискорення тіла ( характеристики обертальної складової руху).

Як полюс можна вибирати будь-яку точку фігури. При зміні точки, вибраної за полюс, характеристики поступальної складової руху змінюються (швидкість і прискорення іншої точки фігури в загальному випадку будуть відрізнятися від і ), а характеристики обертальної складової руху і залишаються незмінними (оскільки яка-завгодно пряма перерізу, паралельного площині П при плоскопаралельному русі твердого тіла повертається на один і той же кут).