50

М инистерство образования и науки Украины

Национальный авиационный университет

Аэрокосмический институт

Кафедра конструкции летательных аппаратов

ЛЕКЦИЯ № 3 (3)

По дисциплине "Конструкция и прочность летательных аппаратов"

3. Нагрузки самолета при выполнениИ маневров

Составитель профессор А.И. Радченко

Киев 2009

3.1. Силы, действующие на самолет в полете

В полете на самолет действуют: (рис. 3.1):

- тяга двигателя Р;

- аэродинамические силы — подъемная сила Y и лобовое со­противление Q;

- сила тяжести G.

Эти силы показаны для самолета, рассматриваемого в виде материальной точки.

В общем случае силы, действующие на самолет, не находятся в равновесии. Однако если к движущемуся с ускорением телу прило­жить силы инерции m_j и mj_n, где т — масса, а m_j и mj_n — тангенци­альное и нормальное ускорения соответственно, то согласно прин­ципу Д'Аламбера можно считать, что такое тело находится в рав­новесии.

все силы, действующие на самолет, объединяют в две группы — поверхностные и массовые.

поверхностные силы это аэродинамические силы и сила тяги. массовые силы - силы тяжести и инерционные.

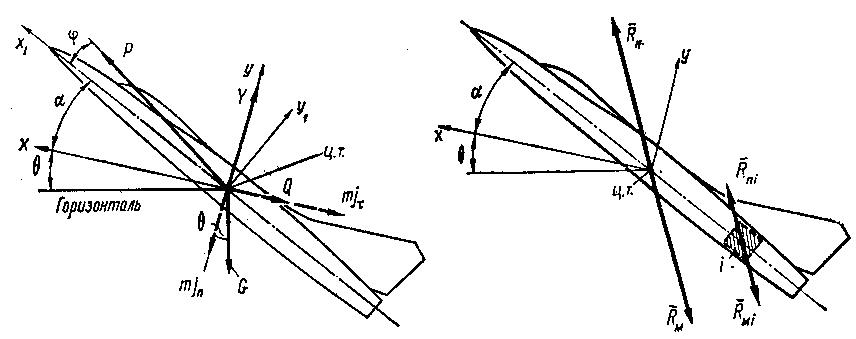
Рис. 3.1 Силы действующие на самолет Рис. 3.2 Поверхностные и массовые силы

На рис. 3.1 показаны:

х₁у₁z₁ - связанная система координат. Она проходит через центр тяжести и связана с продольной осью самолета;

хуz – поточная система координат. Ось Х является касательной к траектории полета в данный момент.

 - угол атаки крыла;

 - угол действия силы тяги.

На рис. 3.2 R_n - равнодействующая поверхностных сил Р, Y и Q;

 R_M - равнодействующая массовых силы G, mj_x, mj_n.

Из условия равновесия сил, действующих на самолет, следует, что равнодействующая поверхностных сил равна равнодействующей массовых сил.

Силы, действующие на отдельные агрегаты самолета, можно раз­бить на те же группы. Для агрегата, расположенного внут­ри самолета, поверхностными силами будут силы реакций, которые возни­каютв узлах крепления его к конструкции.

Для любого агрегата, как и для всего са­молета, справедливо равенство (рис. 3.2):

R_Пi = — R_Мi,

где R_Пi и R_Мi - равнодействующая соответственно поверхностных и массовых сил i-го агрегата.

3.2. Понятие перегрузки

Коэффициентом перегрузки (перегрузкой), называют отношение равнодействующей поверхностных сил к силе тяжести самолета g:

(3.2)

Перегрузку можно выразить также через массовые силы:

(3.3)

Перегрузка показывает, во сколько раз равнодействующая поверх­ностных (массовых) сил больше или меньше силы тяжести самолета.

Перегрузка - величина векторная. Ее направление совпадает с направлением равнодействующей поверхностных сил. На прак­тике обычно пользуются не полной перегрузкой п, а ее проекциями на оси поточной (х, у, z) или связанной (х₁ у₁, z₁) системы координат.

Перегрузкой в данном направлении называют отношение проек­ции равнодействующей поверхностных сил на это направление к силе тяжести самолета. При этом исползуют следующие обзначения перегрузок:

нормальная (поперечная) перегрузка

;

тангенциальная (продольная) перегрузка

;

боковая перегрузка

Здесь R_x, R_y и R_z— проекции равнодействующей поверхностных сил на координатные оси х, у и z соответственно.

Полная перегрузка п связана с ее составляющими соотношением

(3.4)

Зная перегрузку и вес, можно определить силы, действующие на самолет и отдельные его агрегаты.

Например, если пренебречь со­ставляющей силы тяги на ось у, то подъемная сила,

(3.5)

а массовая сила от веса груза или агрегата, например от веса двига­теля G_ДВ,

.

Знак «минус» здесь указывает на то, что сила Р_дв направлена в сторону, противоположную действующей перегрузке.