§3. Дискретный принцип максимума

В этом параграфе приведем дискретный аналог принципа максимума Понтрягина, рассмотренного в §5 раздела 3, который, как будет видно из дальнейшего изложения, не является прямым отображением материала третьего раздела на дискретное время. Более того, как показано в [5], простой перенос формулировки принципа максимума из непрерывного случая в дискретный не дает ни необходимых, ни достаточных условий оптимальности.

Поскольку процесс развития многих прикладных (реальных) управленческих задач отслеживается в дискретные моменты времени, то дискретный принцип максимума имеет весьма широкое применение на практике.

Дискретный принцип максимума сформулируем для управляемой системы с дискретным временем, заданной соотношениями:

, , (5.30)

, (5.31)

, . (5.32)

Здесь, как и в предыдущем параграфе, – фазовый вектор, – вектор управления в момент времени t, , , – функция, описывающая изменение фазового состояния системы, – фиксированный вектор начального состояния в момент .

Последовательность , удовлетворяющая условиям (5.32), является допустимым управлением, а соответствующая этому управлению траектория системы (5.30)-(5.31) – допустимой траекторией.

В качестве целевого функционала будем рассматривать терминальный критерий вида:

. (5.33)

Допустимое управление и соответствующая ему траектория , которые доставляют наименьшее возможное значение критерию качества (5.33), являются соответственно оптимальным управлением и оптимальной траекторией задачи (5.30)-(5.33).

Будем считать, что функции , , и F непрерывны (соответственно в пространствах и ) и имеют непрерывные частные производные по x. Пусть, кроме того, множество U компактно в .

Как и в непрерывном случае (см. §5 раздела 3), для доказательства теоремы о принципе максимума в задаче (5.30)-(5.33) нам понадобятся понятия приращения критерия качества (5.33) и приращения допустимого управления (игольчатой вариации).

Рассмотрим наряду с оптимальным управлением задачи (5.30)-(5.33) другое допустимое управление , такое что , . Определим приращение критерия (5.33):

(5.34)

где – траектория системы (5.30)-(5.31), соответствующая управлению , , .

Возьмем произвольную последовательность , где , . Если , то справедливо тождество

. (5.35)

Положим:

. (5.36)

Тогда из (5.34) и (5.35) получим:

. (5.37)

Поскольку приращение траектории удовлетворяет уравнению

(5.38)

то, введя обозначения

,

,

можно записать:

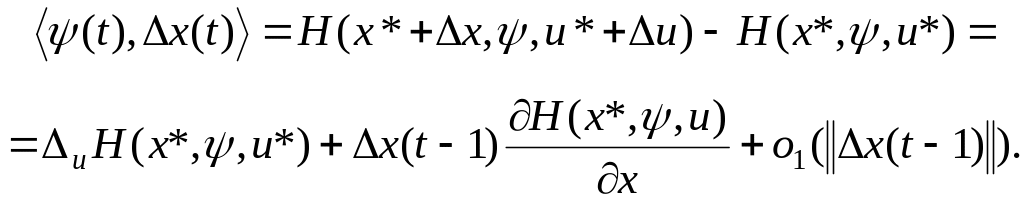(5.39)

Функция H представляет собой функцию Понтрягина для дискретной задачи оптимального управления (для сравнения см. (3.24)).

Соотношение (5.39) подставим в (5.37) и положим:

, . (5.40)

Получаем формулу приращения критерия качества:

,

где ,

, ,

.

Соотношения (5.36), (5.40) образуют сопряженную систему для дискретной задачи оптимального управления (сравните с системой (3.25) для непрерывного случая).

Подобно §5 раздела 3 введем аналог игольчатой вариации управления:

(5.41)

Подставив эту функцию в уравнение (5.38), имеем:

, ,

, (5.42)

, .

Следовательно,

, (5.43)

где

для некоторого . При этом .

Если , а функция – вогнутая, то , , т.е.

,

что означает (см. теорему 3.6) выполнение условия максимума

, , (5.44)

для оптимального управления .

Если же предположения о свойствах функций f, F не выполняются, то условие (5.44) не следует из и формулы (5.43), т.е. вариация (5.41), в отличие от непрерывного случая, не позволяет доказать принцип максимума для задачи (5.30)-(5.33). Это объясняется тем, что в системах с непрерывным временем параметр  игольчатой вариации мог выбираться сколь угодно малым (см. §5 раздела 3). В дискретных системах длина отрезка времени, на котором можно независимо варьировать управления, не может быть меньше шага разбиения.

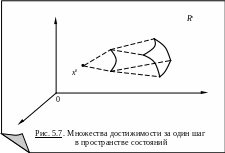
Множество обобщенных скоростей

(5.45)

назовем множеством достижимости за один шаг (см. рис. 5.7).

Теорема 5.6 (дискретный принцип максимума). Пусть

,

– оптимальные управление и траектория задачи (5.30)-(5.33),

– траектория сопряженной системы (5.36), (5.40) и пусть множество выпукло. Тогда для управления , траекторий и выполняется условие максимума (5.44).

Доказательство. Предположим, что теорема неверна, т.е. при некоторых , выполняется неравенство:

.

В силу выпуклости множества (5.45) найдется вектор-функция , , удовлетворяющая равенству:

(5.46)

(см. рис. 5.8).

Подставим в (5.42) вместо v. Тогда , , т.е. . Если равенство (5.46) подставить в (5.43), то получим:

.

При достаточно малых отсюда следует, что , а это противоречит оптимальности последовательности . Теорема доказана.

В теореме 5.6 принцип максимума сформулирован как необходимое условие оптимальности. Покажем, что предположение выпуклости (5.45) существенно для справедливости этой теоремы.

Пример 5.6. Рассмотрим следующую задачу оптимального управления:

,

, ,

.

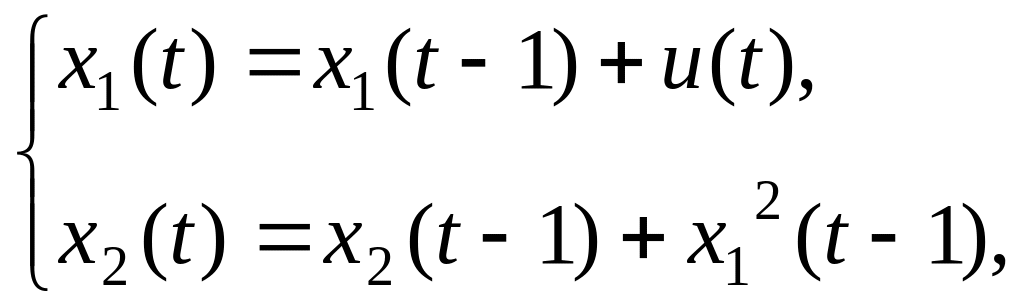
Оптимальным управлением для этой задачи является , но оно не удовлетворяет принципу максимума. Действительно,

,

а сопряженная система записывается в виде:

, .

Отсюда вдоль оптимальной траектории , получаем , . Значит, , а эта функция на множестве в точке достигает не максимума, а минимума.

Как видим, выпуклость множества (5.45) играет важную роль в формулировке принципа максимума.

Покажем класс задач, где выпуклость множества (5.45) заменяется в теореме 5.6 выпуклостью множества U.

Пусть процесс описывается уравнениями вида:

, , (5.47)

где – матрицы размера , при ограничениях (5.31), (5.32) и критерии качества (5.33). При этом вектор-функции , непрерывны и имеют непрерывные частные производные. Заметим, что правая часть (5.47) – линейная функция по управлению.

Теорема 5.7. Если U – выпуклое множество, то для оптимального управления задачи (5.47), (5.31)-(5.33) справедливо условие максимума, имеющее вид:

, .

Доказательство теоремы вытекает из выпуклости U и линейности правых частей (5.47) относительно u. Множество (5.45) в этом случае имеет вид и является выпуклым, так как линейное преобразование сохраняет свойство выпуклости.

Аналогичные результаты можно получить и для задачи оптимального управления с условиями (5.30)-(5.32) и интегральным критерием качества вида:

, (5.48)

т.е. для задачи

, ,

, , , (5.49)

.

Для формулировки теоремы о принципе максимума в этом случае вводится дополнительная координата :

.

Для каждого момента t эта величина оценивает суммарное качество процесса за все предыдущие моменты времени в соответствии с критерием (5.48). При этом уравнение движения и краевые условия для запишутся в форме:

,

, .

В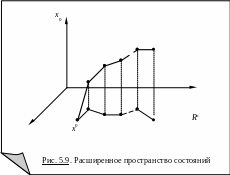 результате получается расширенное пространство состояний , элементами которого являются векторы вида , где (рис. 5.9).

Функция Понтрягина для задачи (5.49) имеет вид:

, (5.50)

а сопряженная система задается уравнениями:

, ,

.

Решение этой системы обозначим через .

Для произвольного вектора расширенного пространства введем множество:

. (5.51)

Теорема 5.8. Пусть множества (5.51) выпуклы при любых . Тогда оптимальное управление доставляет максимум функции Понтрягина (5.50):

.

Доказательство этой теоремы можно найти в [33].

Следствие. Если множество U выпукло, а функция Понтрягина вогнута по u при любых  и x, то она всегда достигает максимальное значение на оптимальном управлении.

В частности, это утверждение выполняется для задачи (5.49), в которой закон движения задан в форме линейных по u уравнений (5.47), функция выпукла по u, множество U выпукло. Функция Понтрягина здесь имеет вид:

и является вогнутой по u при любых  и x. Тогда множество выпукло, а значит, на оптимальном управлении справедливо утверждение теоремы 5.8.

До сих пор мы рассматривали принцип максимума как необходимое условие оптимальности. Однако существуют управляемые системы, для которых дискретный принцип максимума является не только необходимым, но и достаточным условием. Например, к ним относятся линейные (как по x, так и по u) задачи оптимального управления с дискретным временем.

Рассмотрим задачу:

(5.52)

(5.53)

(5.54)

. (5.55)

Теорема 5.9. Пусть – выпуклая по u и по x функция, U – выпуклое множество. Для того чтобы в задаче (5.52)-(5.55) управление было оптимальным, необходимо и достаточно, чтобы функции

(5.56)

достигали максимального значения по при на этом управлении. Значения здесь определяются из сопряженной системы:

, .

Доказательство. Необходимость. Так как задача (5.52)-(5.55) является частным случаем задачи (5.49), воспользуемся следствием из теоремы 5.8. В задаче (5.52)-(5.55) уравнения закона движения линейны по u, функция выпукла по u, множество U выпукло. Поэтому оптимальное управление доставляет максимум функции Понтрягина.

Достаточность. Представим критерий качества (5.55) как функцию управлений , заданных посредством соотношений (5.52) на выпуклых множествах (5.54) при каждом начальном состоянии (см. §2 этого раздела). Для этого последовательно используем уравнения (5.52), в результате каждое состояние запишется как линейная комбинация управляющих воздействий:

, (5.57)

где , . При этом выпуклая по , функция после линейной замены (5.57) становится функцией, выпуклой по переменным , ..., . Поэтому функция Понтрягина (5.56) вогнута по u при каждом начальном состоянии (5.53) и имеет единственную точку максимума на выпуклом множестве U. При этом функция выпукла по u и имеет на выпуклом множестве единственную точку минимума .

Замечание. Теорема 5.9 остается справедливой, если вместо (5.52) уравнения движения имеют вид:

при произвольном множестве U. Для этого нужно потребовать, чтобы множество было выпуклым. Это вытекает из того, что данная задача приводится к постановке (5.52)-(5.55) путем замены , :

, ,

, ,

,

где в качестве в каждый момент t выступает единичная матрица.

Приведем схему применения дискретного принципа максимума для задачи (5.52)-(5.55) (сравните со схемой в §9 раздела 3).

Этап 1. Применить условие принципа максимума, т.е. найти максимум функции Понтрягина (5.56) по допустимым управлениям.

В результате определим оптимальное управление как функцию x и :

, . (5.58)

Этап 2. Решить систему, составленную из уравнений движения исходной задачи и уравнений сопряженной системы при управлении (5.58):

, ,

.

Заметим, что закон движения представляет собой последовательность рекуррентных уравнений с начальным условием для момента и прямым ходом времени, а сопряженная система – последовательность рекуррентных уравнений с обратным ходом времени и "начальным" условием для момента . В результате второго этапа получаем общий вид оптимальной фазовой траектории , соответствующей управлению (5.58), и решение сопряженной системы .

Этап 3. Подставить найденные на втором этапе и в соотношения (5.58).

На этом этапе получаем окончательный вид оптимального управления .

Рассмотрим простой пример, иллюстрирующий применение дискретного принципа максимума [33].

Пример 5.7. Пусть в задаче (5.52)-(5.55) , т.е. – скаляры, а критерий качества, который нужно минимизировать, имеет вид:

,

где и . Для данного случая

.

Построим функцию Понтрягина:

.

Множество выпукло, функция квадратичная и строго выпуклая (для проверки можно найти матрицу вторых производных, которая будет диагональной и положительно определенной). Условия теоремы 5.9 здесь выполнены, поэтому оптимальный процесс полностью определяется следующими соотношениями:

, ,

где .

Таким образом, для решения дискретных задач оптимального управления, как и в непрерывном случае, можно использовать принцип максимума. Он не является точной копией формулировки принципа максимума для непрерывного случая, но сохраняет ряд общих с ним черт, предоставляя необходимые, а в некоторых случаях и достаточные условия оптимальности и тем самым позволяя найти решение многих задач.